Mattegåta
Visa att varje andragradspolynom kan skrivas som en summa av två andragradspolynom, vars diskriminanter är lika med 0.
Diskussion
Vad var en diskriminant? För ett polynom Ax²+Bx+C är det talet B²-4AC.
Ifall diskriminanten är positiv, så har ekvationen Ax²+Bx+C=0 två reella rötter. Ifall den är negativ, så har ekvationen inga reella rötter. Om diskriminanten är 0, har ekvationen exakt en reell lösning.
Bilden illustrerar hur graden för ekvationen kan se ut i de olika fallen (D betecknar diskriminanten).
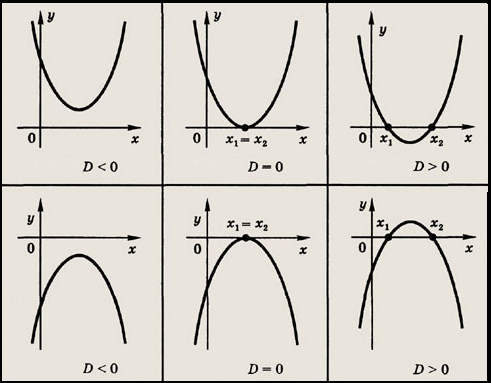
Nu när vi har koll på diskriminanten, kan uppgiften lösas grafiskt eller algebraiskt, vilken man nu föredrar. Nedan är en algebraisk lösning presenterad.
Lösning (av Benjamin Fayyazuddin-Ljungberg)
Låt P(x) vara polynomet vi vill skriva som summan av två andra polynom. Om P(x) = Q(x) + R(x) är kP(x) = kQ(x) + kR(x). Om Q(x) har diskriminant noll har kQ(x) också det. Därför kan vi utan inskränkning anta att P(x) har koefficienten 1 framför x²-termen.
Nu betraktar vi tre fall:
1) P(x) har diskriminant noll. Då har vi inga problem: P(x) = P(x)/2 + P(x)/2
2) P(x) har negativ diskriminant, det kan skrivas som (x-a)² + k² för någon konstant k. Låt z=x-a, så P(x) = z² + k². Då kan vi skriva P(x) som (z+k)²/2 + (z-k)²/2 = (x-a+k)²/2 + (x-a-k)²/2. Det är tydligt att de här polynomen bara har ett nollställe var, alltså är diskriminanten noll.
3) P(x) har positiv diskriminant, det kan skrivas som (x-a)² – k² för någon positiv konstant k. Låt z = x-a igen. Då är P(x) = z² – k². Vi skriver P(x) som 2(z-k/√2)² – (z-k√2)² = 2(x-a-k/√2)² – (x-a-k√2)². Dessa har också bara ett nollställe var, så de har diskriminant noll.
Relaterade


Min tanke. Enligt algebrans fundamentalsats så kan vi faktorisera ett godtyckligt polynom som p(x) = c *(x-a)(x-b)….. Så i vårt fall, säg att vi har p(x) = c*(x-a)(x-b) för godtyckliga a,b och c \in C. Om diskriminanten är noll så har en andragradsekvation en dubbelrot, så betrakta:: c(x-u)^2+c(x-v)^2 = c((x-u)+i(x-v))(x-u)-i(x-v)). Vi vill nu att x = a skall ge ett nollställe, samt x = b. Detta ger upphov till ett ekationssystem, som om vi löser det, ger upphov till lösningarna u = (1/2-i/2) b + (1/2+i/2)a, v = (1/2-i/2) a + (1/2+i/2)b.
Detta tycks (för mig) fungera, men jag kan ha fel. Någon tanke?
u,v måste väl vara reella också? Jag tror inte att de nödvändigtvis blir det i din lösning. Till exempel blir u och v ickereella om a, b är reella och a \neq b. Däremot tror jag att lösningen fungerar när diskriminanten är ickepositiv. Då är a och b varandras konjugat, och de imaginära delarna blir noll.
Sen vill jag bara lägga till att din nya summa blir c/2 ((x-u)² + (x-v)²). Som du skrev får du 2c som koefficient framför x².
Hm, jag kanske inte förstår dig riktigt. Jag håller dock med om att summan är c/2, du har helt korrekt där.Tack så mycket! Du har troligen korrekt på det andra, vill bara kolla var jag har gjort fel. Jag ser inget behov av att låta u och v vara reella, diskriminanten är väl ändock noll här? Om jag inte minns fel så försvinner diskriminanten om och endast om andragradsekvationen har multipla lösningar i splittringskroppen. Om vi t.ex. betraktar fallet för ett polynom med rötterna tre och två, så får vi: http://www.wolframalpha.com/input/?i=3/2(x-((1/2-i/2)*3+%2B+(1/2%2Bi/2)*2))^2%2B3/2((x-((1/2-i/2)*2+%2B+(1/2%2Bi/2)*3))^2 enligt formeln tidigare beskriven. Diskriminanten av de två andragradspolynom det till slut blir, 3/2 (x-(5/2+i/2))^2 respektive 3/2 (x-(5/2-i/2))^2 är väl ändå noll? WolframAlpha och mathematica verkar tycka det.
Tack för att du har tagit dig tid att kika igenom och jag hoppas att du har tid att kolla igenom detta. Om det verkar helt snurrigt så får du ursäkta, eller om jag begår några hemska misstag.
Just ja, glömde nämna att jag ville ha koefficienten, c till 3. Så 3(x-2)(x-3) menade jag kunde skrivas sådär.
Vad vidare så tyckte jag att detta var en fin uppgift.
Du har självklart rätt. Jag uppfattade problemet som att man skulle skriva ett reellt andragradspolynom som summan av två andra reella andragradspolynom, men det står ju faktiskt inte att de ska vara rella.
Kul att ni tyckte om uppgiften!
Egentligen tänkte jag själv på att polynom skulle ha reella koefficienter (om jag inte specificerar något så är det oftare det ”vanligare” fallet eller vad man ska säga), därav bilderna ovan.
Men uppgiften blir inte särskilt mycket enklare av att anta att vi betraktar polynom över de komplexa talen, så bra jobbat M och tack för en alternativ lösning!