Tävlingen vårterminen 2011 här på bloggen innehöll hela 30 uppgifter, här kan ni titta på alla problemen igen och kolla upp lösningarna:
Kuben – Siffertriangeln
Rebusen – Schackcirkeln
Blommor – Familjealbum
Punkter – Trasig våg
Syskon – Sannoliketer
Kaniner – Staket
Fången – Speciellt tal
Papper – Brickor
Hexagonen – Siffersumman
Nötter – Äpplen
Cirkelkonstruktion – Cosinussumman
Uttrycket – Ön
Cthulhu – Tabellen – Stenhögarna
Matchen – Dvärgarna – Rutnätet
Många deltagare har skickat in flera lösningar och jag har försökt att välja ut de bästa. Bidrag som har vinstchans har valts ut från helt korrekta lösningar och bedömts efter originalitet och hur pass förståeliga de var. Jag tog bara med uppgfter som var värda minst 2 poäng. Varje person (förutom Skägget, som redan har vunnit) som hade skickat in minst en sådan lösning tävlar om att vinna ett pris.
Man tävlar med sitt bästa (i mitt högst subjetiva tycke) bidrag. Jag vill utmärka David och Thomas (och Skägget), som skickade in väldigt många bra lösningar, det var faktiskt väldigt svårt att välja deras bästa respektiva lösning.
Skriv gärna i kommentarerna vilket eller vilka bidrag du tycker bäst om! Du får givetvis rösta anonymt och du får rösta på din egen lösning. Rösta senast på måndag den 27 juni.
Bidrag 1
Nej, det går inte.
Om man delar upp varje rad om tre så ser man direkt att fyra av siffrorna kommer att användas i tre rader, dvs tre ggr. De övriga siffrorna kommer att användas en gång vardera. För att alla raderna skall ge samma summa så måste den totala siffersumman vara delbar med 6 (eftersom det är 6 st rader). Det betyder att 3A + 3B + 3C + 3D + E + F + G + H + I + J skall vara delbart med 6. Vi vet att Siffersumman av talen 0-9 = 45, som ger en rest 3 när vi delar med 6. Det ger oss att 2A + 2B + 2C + 2D + 3 skall vara delbart med 6. 2A, 2B, 2C och 2D är alla jämna tal (2*0 är kanske inte ett jämnt tal, men det är åtminstone inte ojämnt). Fyra jämna tal (varav ett kanske är 0) plus ett ojämnt tal (3) ger en ojämn summa. Ett ojämnt tal är inte delbart med 6. Så det går inte att fylla i siffertriangeln så att alla summor är samma.
Bidrag 2
Vi tänker oss att vi räknar modulo 2. En ”balanserad” utplacering av 0,..,9 ger en balanserad placering modulo 2. Vi antar att det står noll överallt från början och placerar ut 1:or en i taget. Då varje nod ligger på antingen en kant eller tre kanter så kommer varje utplacerad 1:a att ändra pariteten på ett udda antal kanter. Då vi har 5 ettor så har vi totalt ett udda antal paritetsändringar. Men då kanterna skulle ha samma värde mod 2 så krävs det ett jämnt antal paritetsändringar (alla ska antingen stanna på värde noll eller så ska sex st kanter ändras till värde 1).
Bidrag 3
Den största möjliga cirkeln har radien:
0,5s^2+1,5s^2=2,5s^2 Radien blir då: Roten ur 2,5s^2
s motsvarar sidlängden på en schackruta.
Det går inte att göra en större cirkel eftersom för alla cirklar som bara går genom svarta rutor så behöver de gå genom ett hörn för att ta sig från en svart ruta till en annan. I min cirkel som jag anser vara den största möjliga behöver cirkelns rand löpa genom totalt åtta hörn och två hörn på rad. Nästa större cirkel som man kan försöka på innehåller 3 hörn på rad. Har man tre punkter på en rad som cirkelns rand måste gå igenom blir det ingen cirkel utan bara ett rak linje. Så en kvartscirkel kan bara passera genom två hörn för att fortfarande kunna vara en cirkel.
Bidrag 4
Motsägelsebevis att största möjliga radie är rot(1,5^2+0,5^2):
För att cirkeln skall vara stor måste den gå genom mer än en svart ruta. Då måste den passera genom hörn. Från och med nu koncentrerar jag mig på vilka hörn den kan gå genom. När cirkelns rand går in genom ett hörn till en ruta kan det antingen gå ut genom det diagonalt motsatta eller ett närliggande hörn.
Då använder jag följande konstateranden:
1: Om randen gick genom diagonalt motsatta i föregående ruta kan det inte igen gå genom diagonalt motsatta. Då skulle de tre hörnen vara kolinjära och radien oändlig.
2: Om den går genom närliggande hörn två gånger i rad blir diametern rot(0,5^2+0,5^2).
3: Bästa resultat blir om det alternerar: varannan i motstående diagonalt och varannan i närliggande. Då blir radien enligt ovan.
Bidrag 5
Det finns exakt två cirklar som kan ritas. För att rita den ena tar man en vit ruta och ritar den omskrivna cirkeln. För den andra, väljer vi en svart rutas mittpunkt som mittpunkten på cirkeln. Nu konstruerar vi en större cirkel, och visar att det är den enda andra cirkeln som kan ritas.
För att en cirkel ska kunna uppfylla kraven som ställs måste den passera genom hörn på rutor varje gång den passerar från en ruta till en annan. Om den passerade genom en kant, skulle den gå från svart till vitt, som inte tillåts. Vi kallar två hörn på rutor närliggande om de delar en kant, och motsatta om de ligger på samma diagonal. Säg att cirkeln passerar genom tre motsatta hörn på rad. Då finns det en rak linje som förbinder de två hörnen som ligger längst bort från varann. Men på grund av en cirkels form kan ingen annan punkt på cirkeln ligga på den linjen, så det kan inte hända att den passerar genom tre motsatta hörn på rad. Säg nu att den passerar genom tre närliggande hörn på rad. Då har vi tre punkter på cirkeln, som inte ligger på en linje, och vet alltså unikt vad det är för cirkel. Men det är exakt samma cirkel som vi redan konstruerat, som omskriver en ruta!
Alltså måste punkterna alternera mellan närliggande och motsatta hörn. På grund av formen av cirkeln, kan vi bara välja ett av de närliggande hörnen, så det finns bara en möjlighet för en cirkel som inte är den vi redan gjort. Om vi ritar ut de punkterna på ett bräde och använder oss lite av Pythagoras sats för att beräkna sträckor, ser vi att de faktiskt ligger på en cirkel (som delar mittpunkt med en svart ruta). Radien visar sig vara sqrt(5/2) * x, där x är sidlängden på en ruta.
Bidrag 6
Betrakta två godtyckliga staket. Eftersom staketen inte får korsa varandra måste de antingen vara helt separata från varandra eller så ligger det ena inuti det andra. Vi inför en ny regel, man måste bygga staketen inifrån och ut. Alltså om man har byggt ett staket så får man inte bygga nya staket inuti det slutna området. Det gör ingen inskränkning på problemet, det påverkar bara i vilken ordning man bygger staketen. Vi kan börja med att bygga ett staket runt varje hus, det förstör inte våra möjligheter att bygga större staket. Vi säger att ett staket är coolt om det inte har något staket runt sig. Så för tillfället har vi 100 coola staket. Varje nytt staket vi bygger måste omsluta minst två coola staket (om det inte omsluter något staket så kan det inte heller omsluta något hus och om det endast omsluter ett coolt staket så omsluter det nya staketet och det gamla coola staketet samma samling hus). Så i processen när vi bygger ett nytt staket så kommer minst två f.d. coola staket sluta vara coola. I utbyte får vi ett nytt coolt staket, men resultatet är en minskning av antal coola staket. Efter att ha byggt högst 99 staket utöver de 100 första, så är vi alltså nere i endast ett coolt staket och då kan vi inte bygga mer. Så vi kan inte ha fler än 199 staket totalt, det återstår endast att visa att 199 staket är möjligt. Låt oss ha en stad där husen står på rad, numrerade från 1-100. Bygg ett staket runt varje hus, bygg därefter staket som omfattar hus (1,2,3…,n) för varje n från 2 till 100. Totalt 199 staket, fullt möjligt. Svaret är alltså 199.
Bidrag 7
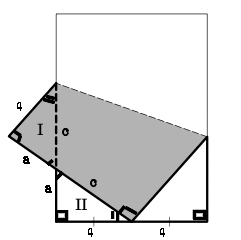
Ty pappret är en rektangel, kan vi identifiera de fyra räta vinklarna.
Enligt vertikalvinkelsatsen är de två vinklar som möts, där de kongruenta tringlarna tangerar varandra, lika.
Vi har nu två trianglar, I och II, med två vinklar lika, vilket betyder att även den tredje är lika. Detta har också stöd i påståendet att trianglarna är kongruenta.
Kortsidan på 8 centimeter delas i två lika delar, vilka då blir 4 centimeter var. Ty II är kongruent med I är även motsvarande sida i triangel I 4 centimeter.
Låt a beteckna den okända kateten i de kongruenta trianglarna och låt c beteckna hypotenusan.
Eftersom a och c till fullo utfyller den nedvikta kortsidan, får vi att a+c=8, enär kortsidan just är 8 centimeter. Pythagoras sats ger även att 4^2+a^2=c^2. Lösningen till detta ekvationssystem är a=3 samt c=5.
Om vi åter viker upp fliken ser vi att längden av långsidan fås av omkretsen av en triangel:
a+c+4=3+5+4=12
Bidrag 8
Ett sådant tal (som jag här kallar för T) kan skrivas som T=12*siffersumman. Talet T är alltså delbart med 2, 3, 4, 6 och 12. Eftersom talet T är delbart med 3 måste även dess siffersumma vara det. Det innebär dock att talet T också måste vara delbart med 9. Det leder till att även dess siffersumma måste det. Om vi då har en siffersumma som är delbar med nio gånger tolv så måste talet T vara delbart med 108.
Det minsta möjliga talet T är 108. 108=12*(1+0+8). Fler tal T med siffersumma 9 kan inte finnas. Vi testar därför siffersumma 18:
18*12=216. Detta tal har dock siffersumma 2+1+6=9. Därför är det inte ett tal vi söker.
27*12=324. Siffersumman är dock fortfarande 9. Ett tresiffrigt tal kan dock inte ha en högre siffersumma än 27 eftersom talet med högst siffersumma är 999. Därför är det meningslöst att leta efter fler tal T bland tresiffriga tal.
1000/12=83,333333333333333333333333333333333333… Siffersummorna för fyrsiffriga tal T kan vara minst 84. Dock kan inget fyrsiffrigt tal ha en siffersumma högre än 9*4=36, så det finns inga fyrsiffriga tal T.
Vi testar femsiffriga: 10000/12=833.33333333333333333333333333333333… Siffersummorna för T kan här inte understiga 834, men inget femsiffrigt tal kan ha en siffersumma som understiger 9*5=35. Alltså är inte femsiffriga tal T möjliga.
Som vi ser här så ökar den minsta möjliga siffersumman för talet T för varje ny siffra tio gånger, medan den maximala möjliga siffersumman för ett tal med det antalet siffror bara ökar med 9. Därför finns det inga möjliga tal T högre än 108.
Svar: Det finns endast ett sådant tal, nämligen 108. Ifall talet 0 räknas så finns det dock två.
Bidrag 9
Om det inte skulle gå skulle det som mest kunna finnas 99 lådor med minst 1 äpple i, 49 med minst 2, 33 med minst 3, …, med minst n, för annars kan vi ta bort äpplen och lådor så att det finns
lådor med n äpplen i varje, och
är större än eller lika med 100.
Som mest kan vi då ha
1 med 99, totalt 01 större än 99
1 med 49, totalt 02 större än 49
1 med 33, totalt 03 större än 33
1 med 24, totalt 04 större än 24
1 med 19, totalt 05 större än 19
1 med 16, totalt 06 större än 16
1 med 14, totalt 07 större än 14
1 med 12, totalt 08 större än 12
1 med 11, totalt 09 större än 11 277
2 med 09, totalt 11 större än 09
1 med 08, totalt 12 större än 08
2 med 07, totalt 14 större än 07
2 med 06, totalt 16 större än 06
3 med 05, totalt 19 större än 05
5 med 04, totalt 24 större än 04
9 med 03, totalt 33 större än 03
16 med 02, totalt 49 större än 02
50 med 01, totalt 99 större än 01 473
Antalet äpplen blir då 473, och 473 < 2000. Så med 2000 äpplen går det.
Bidrag 10
Om Nord vinner då är a),b),c) och d) sanna.
Om det är oavgjort så är a), c) och e) falska (då tre mål ej kan fås vid oavgjort).
Alltså eftersom att exakt 3 ska vara sanna, måste Syd vinna, eftersom ingen av de andra fallen fungerar.
Då c) och d) inte kommer vara sanna om Syd vinner måste rästen vinna. Så syd släpper in mål och det görs exakt 3 mål i matchen och syd vinner. så då måste det bli 2-1 till syd.

Många fina lösningar här, men min röst får nog gå till Bidrag 6.
Vill också ge ett hedersomnämnande till Bidrag 2 för ett mycket kortfattat och elegant bevis.
Min röst går till bidrag fem.