Universitetsmatte – Sida 2

So you think you can derive?

Jag hjälper en person med att förbereda sig inför en tenta i endimensionell analys och vi träffar på följande tentauppgift:

$\text{Derivera} \ \ x^{\sin x}$

Tror du att du kan derivera rätt på första försöket? Prova och se om du lyckas!

Visa svaret

Matematikerns klagan

Vad vore matematiken utan bevis?
Inte riktig matematik, tycker många och artisten Skägget håller med, när han sitter och lider igenom kursen i Sannolikhet och statistik.

Hans senaste låtkreation heter Matematikerns klagan och är en kampsång för ren matematik.

Text och musik: Skägget

Hör upp, bröder, ni matematiker,
på denna min kvalfyllda låt!
Den kursen jag läser mig plågar ihjäl,
ja jag tror snart jag faller i gråt

För det svider i själen, jag dör lite grann
för var sats som går utan bevis,
och när allting jag får är en formel,
det är som gymnasiet gick i repris

Och jag orkar ej mer, nej bespara mig det här,
för jag vet inte ens vad jag gör,
ty i formelhäftet finns svaret
men ingen förklaring varför

Jag finner ett par variabler
som sägs ha nån slags relevans,
och slår upp tio tusen tabeller
för att finna mitt värde nånstans

Så dammar jag av miniräknaren
som jag sen gymnasiet har kvar,
och ger upp alla mina principer
och beräknar numeriskt mitt svar

Men jag orkar ej mer, nej bespara mig det här,
jag vet inte ens varför det går,
men i formelhäftet finns svaret
så jag gör väl precis som det står

Jag som trodde jag var här för att lära mig nåt
– än har jag inte lärt mig ett skvatt!
För vad hjälper en formel jag inte förstått?
Jag ger upp nu och utropar att:

Jag vill va’ en sann matematiker
som bevisar själv allt han vill ha,
och som fäktas mot världens mysterier
med en värja av ren algebra!

Så slut upp bakom mig och vi seglar iväg
på ett stormande renlärigt hav,
med ett skepp som vi bygger från grunden,
med axiomen Euklides oss gav

För jag orkar ej med en till dag av det här,
nej, jag vet inte ens vad jag gör,
ty i formelhäftet finns svaret
men ingen förklaring varför
Ja, i formelhäftet finns svaret,
och matematikern inom mig dör

Planära grafer

I ett sällskap med många personer kan man leka en lek som kallas ”knuten”. Alla ställer sig i en ring och sluter ögonen. Sedan sträcker alla fram båda sina händer och börjar gå mot mitten. Alla ska ta tag i två andra händer med sina egna.

Efter att alla är klara med det öppnar man ögonen. Målet är nu att lösa upp ”knuten” som bildats utan att släppa taget med händerna. Det gäller att bilda en stor ring igen (det kan också hända att det blir flera ringar).

Ett liknande spel är Planarity, fast personerna i spelet kan ha fler än två händer. Målet är att lösa upp all tilltrassel så att inga par av händer måste hållas över varandra.

Personer är representerade med punkter och en kant som går mellan två punkter visar att de två personerna håller handen. Alla spelande har väldigt uttänjbara händer. Försök att klara några nivåer! (Jag kom till Level 7.)

Sådana här bilder kallas grafer, om de går att ”plana ut” på det här snygga sättet (så att inga två kanter korsar varandra) kallas de planära. Det är svårt att se direkt huruvida en graf är planär eller inte, däremot uppfyller alla planära grafer följande formel.

Eulers formel

En graf är ritad på ett plan på så sätt, att inga två kanter korsar varandra. Om V är antalet hörn i grafen, E – antalet kanter och F – antalet områden som planet delas upp i, så gäller:

V – E + F = 2

Att det blev just talet 2 beror på att man ritade på ett plan. Ritar man grafer på andra konstiga ytor blir det ett annat specifikt tal just för denna yta. Det talet kallas ytans eulerkaraktäristik.

Lektioner från kollot

Snart är sommaren slut för min del och det är dags att sammanfatta vad jag lärt mig under mattekollotiden (jag var lärare för några av Rysslands mest skärpta åttor):
1. Åttan är lite för tidig årskurs för att introducera begreppet grupp.
2. Komplexa tal definieras bäst som mängden av par av tal plus regler.
3. Ha med några stycken 15-spel när du undervisar om permutationer!
4. 2x2x2 – Rubiks kuber som smycken är snyggt.
5. Om man är oförsiktig i sina matteresonemang kan man missa att man egentligen behöver använda satsen om att maximum på kompakt mängd existerar.

Förutom det har jag lärt mig att föra krig mot getingar, gå upp 5 minuter innan lektionerna börjar och hitta dold matematisk betydelse i ryska poplåtar.

Klassiska bevis: Randvinkelsatsen

Många har hört talas om den beryktade randvinkelsatsen. Eventuellt har du träffat på den på gymnasiet. Men få har egentligen koll på hur man bevisar satsen.

Om du vill komma fram till beviset själv med hjälp av några ledande uppgifter, se Cirklar och randvinklar. Annars läs vidare här.

Sats (Randvinkelsatsen)

Markera tre olika punkter A, B och C på en cirkel. Markera även cirkelns mittpunkt O. Då är vinkeln AOC dubblet så stor som vinkeln ABC.

Bevis

Man ska vara väldigt försiktig och rigorös med geometriska bevis. Med det menas att alla möjligheter för bildens utseende ska undersökas, om man nu ska rita någon bild överhuvudtaget.

Så till exempel, kan det se ut så här:

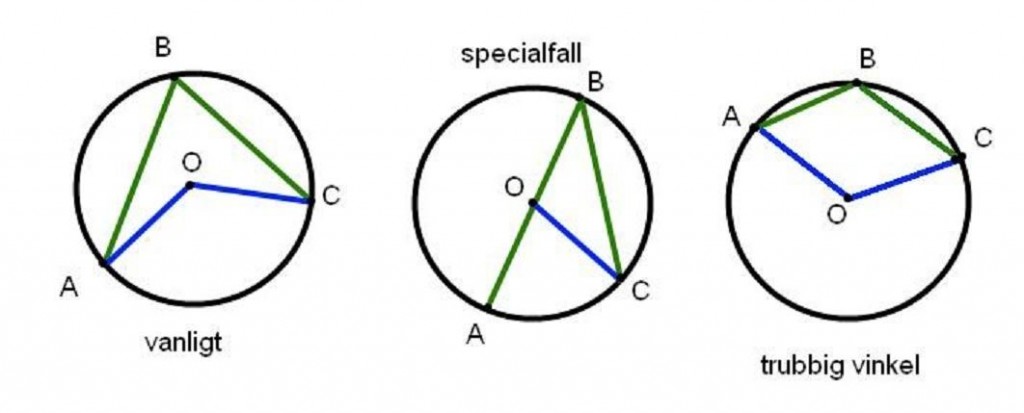Så hur ska man täcka alla möjligheterna på ett bra sätt? Det beror förstås på vad man tänker baser beviset på.

Oftast betraktas bilderna som väsentligen olika om olika skärningar mellan linjerna äger rum. I bevisen grundar vi ofta resonemang på hur olika objekt ligger i förhållande till varandra och inte så mycket på storlekarna på vinklar, cirkelbågarna etc.

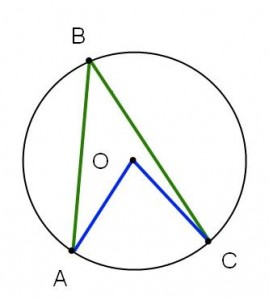
Med detta sagt väljer vi således att betrakta tre fall (som täcker alla möjliga situationer):


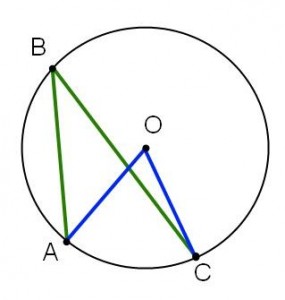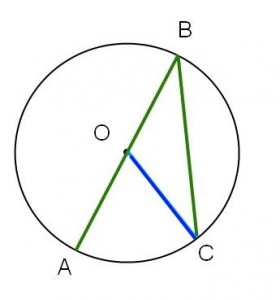
Fall I	Fall II	Fall III

Fall I: Vinkel AOC ligger helt inuti vinkeln ABC.
Fall II: Detta är specialfallet då vinkeln AOC delar sida med vinkeln ABC.
Fall III: Två av vinklarnas sidor skär varandra.

Fall II

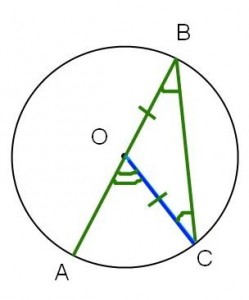
Detta fall verkar vara enklast, så vi börjar med det. OB=BC för att de är radier, så $\triangle COB$ är likbent. Alltså gäller $\angle OBC = \angle OCB$ .

$\angle AOC + \angle BOC = 180\textdegree$ men också $\angle OBC + \angle OCB + \angle BOC = 180\textdegree$ .
Då måste $\angle AOC = \angle OBC + \angle OCB = 2\angle OBC$ . Vilket skulle bevisas.

Fall I

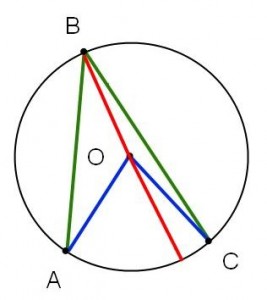
Första fallet då? Vi ”fuskar lite” och drar en hjälplinje. Men nu får vi egentligen Fall II igen! Tillämpa det på varje halva av bilden och addera.

Fall III

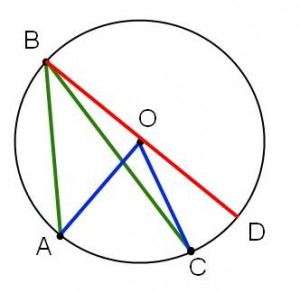Fall III måste väl vara svårare? Inte då! Vi ”fuskar” och drar en hjälplinje igen. Vi får återigen på grund av Fall II att $2\angle DBA=\angle DOA$ och att $2\angle DBC=\angle DOC$ . Subtrahera det andra resultatet från det första och vi är klara!

Den bästa låten om ringar

Jag är stolt över att få presentera låten, som redan är känd för många matematikstuderande vid Uppsala Universitet.

Texten är baserad på innehållet i kursen Algebra II, där mycket ringteori ingår.

Låten heter just Ringteori och stilen är trallpunk.

Text och musik: Erik Svensson

En ring är en mängd och två funktioner,
och som krav ställs på dessa därvid
att det är en abelsk grupp med additionen,
och med gånger en monoid

En ring är en mängd…

Och distributiv ska den vara
men ej tvunget kommutativ, nej!
Exempelvis kvaternioner
och matriser kommuterar ju ej (generellt)

Men antag att den kommuterar,
och att för alla nollskiljda a
finns ett b så att a gånger detta
blir ett, då kallas ringen en kropp, hipp hurra!

För en kropp är så trevligt behändig,
och den har endast två ideal,
varav ena är hela kroppen
och den andra är trivial

En ring är en mängd…

Och mellan två ringar kan hända
att det finns en isomorfi,
då är de i nån mening en enda,
för strukturen bevaras däri

En ring är en mängd…

Transformationsmatrisen – del 5

Från Transformationsmatrisen – del 4 fick vi följande resultat:

För att bestämma transformationsmatrisen från bas $A$ till bas $B$ , uttryck basvektorerna i basen $B$ och skriv in resultaten som kolonner i en matris.

Hur gör man då det essentiella steget, det vill säga hur uttrycker man vektorerna i $A$ i basen $B$ ?

Jo, precis som på det sista sättet i Transformationsmatrisen – del 3.

Allmänt, ansätt:
$A_1=x_{11}B_1+x_{12}B_2+x_{13}B_3+\dots+x_{1n}B_n$
$A_2=x_{21}B_1+x_{22}B_2+x_{23}B_3+\dots+x_{2n}B_n$
$A_3=x_{31}B_1+x_{32}B_2+x_{33}B_3+\dots+x_{3n}B_n$
$\vdots \vdots$
$A_n=x_{n1}B_1+x_{n2}B_2+x_{n3}B_3+\dots+x_{nn}B_n$

vilket är precis samma sak som $A_1=\left(\begin{array}{c}x_{11} \\x_{12} \\x_{13} \\\vdots \\x_{1n}\end{array} \right)_B, \dots, A_n=\left(\begin{array}{c}x_{n1} \\x_{n2} \\x_{n3} \\\vdots \\x_{nn}\end{array} \right)_B$

(Varför det är så? Se Transformationsmatrisen – del 2.)

Det är alltså de här talen $x_{11}, x_{12}, x_{13}$ och så vidare som vi skall bestämma. De är ju precis talen i transformationsmatrisen från basen $A$ till basen $B$ .

Hur bestämmer man dessa tal?

Notera att varje ekvation i det stora ekvationssystemet är ett ekvationssystem i sig, om man skriver ut alla vektorernas koordinater:

$A_1=\left(\begin{array}{c}a_{11} \\a_{12} \\a_{13} \\\vdots \\a_{1n}\end{array} \right)$ och $B_1=\left(\begin{array}{c}b_{11} \\b_{12} \\b_{13} \\\vdots \\b_{1n}\end{array} \right), B_2=\left(\begin{array}{c}b_{21} \\b_{22} \\b_{23} \\\vdots \\b_{2n}\end{array} \right),\dots, B_n=\left(\begin{array}{c}b_{n1} \\b_{n2} \\b_{n3} \\\vdots \\b_{nn}\end{array} \right)$

(Alla små a:n och b:n är för oss kända tal.)

Då blir den första ekvationen $A_1=x_{11}B_1+x_{12}B_2+\dots+x_{1n}B_n$ ett ekvationssystem:
$a_1=x_{11}b_{11}+x_{12}b_{12}+\dots+x_{1n}b_{1n}$
$a_1=x_{11}b_{21}+x_{12}b_{22}+\dots+x_{1n}b_{2n}$
$\vdots$
$a_1=x_{11}b_{n1}+x_{12}b_{n2}+\dots+x_{1n}b_{nn}$

Och sådana där vet vi löses med Gauss-elimination.

$\left(\begin{array}{cccccc}b_{11} & b_{12} & \dots & b_{1n} & | & a_{11} \\b_{21} & b_{22} & \dots & b_{2n} & | & a_{12} \\\vdots & \vdots & \vdots & \vdots & \vdots & \vdots\\b_{n1} & b_{n2} & \dots & b_{nn} & | & a_{1n} \end{array} \right)$

Det här löses som vanligt. Matrisen till vänster (allt utom det sista kolonnen) ska göras om till en identitetsmatris och när man gjort det blir den högraste kolonnen det man söker, det vill säga $\left(\begin{array}{c}x_{11} \\x_{12} \\\vdots \\x_{1n}\end{array} \right)$ .

Vad gör vi med den andra ekvationen, $A_2=x_{21}B_1+x_{22}B_2+x_{23}B_3+\dots+x_{2n}B_n$ , vilket ekvationssystem blir det?
Jo, om $A_1=\left(\begin{array}{c}a_{21} \\a_{22} \\\vdots \\a_{2n}\end{array} \right)$ , så är det

$\left(\begin{array}{cccccc}b_{11} & b_{12} & \dots & b_{1n} & | & a_{21} \\b_{21} & b_{22} & \dots & b_{2n} & | & a_{22} \\\vdots & \vdots & \vdots & \vdots & \vdots & \vdots\\b_{n1} & b_{n2} & \dots & b_{nn} & | & a_{2n} \end{array} \right)$

alltså med samma vänstra del till matris som förut. Det blir exakt samma Gauss-operationer som ska utföras, vilket betyder att jobb kan sparas.

$\left(\begin{array}{ccccccc}b_{11} & b_{12} & \dots & b_{1n} & | & a_{11} & a_{21} \\b_{21} & b_{22} & \dots & b_{2n} & | & a_{12} & a_{22} \\\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots\\b_{n1} & b_{n2} & \dots & b_{nn} & | & a_{1n} & a_{2n} \end{array} \right)$

$\longrightarrow$

$\left(\begin{array}{ccccccc}1 & 0 & \dots & 0 & | & x_{11} & x_{21} \\0 & 1 & \dots & 0 & | & x_{12} & x_{22} \\\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots\\0 & 0 & \dots & 1 & | & x_{1n} & x_{2n} \end{array} \right)$

Och på exakt samma sätt löser vi ut alla andra små x med hjälp av resten av ekvationerna:

$\left(\begin{array}{ccccccccc}b_{11} & b_{12} & \dots & b_{1n} & | & a_{11} & a_{21} & \dots & a_{n1} \\b_{21} & b_{22} & \dots & b_{2n} & | & a_{12} & a_{22} & \dots & a_{n2} \\\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots\\b_{n1} & b_{n2} & \dots & b_{nn} & | & a_{1n} & a_{2n} & \dots & a_{nn} \end{array} \right)$

$\longrightarrow$

$\left(\begin{array}{ccccccccc}1 & 0 & \dots & 0 & | & x_{11} & x_{21} & \dots & x_{n1} \\0 & 1 & \dots & 0 & | & x_{12} & x_{22} & \dots & x_{n2} \\\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots\\0 & 0 & \dots & 1 & | & x_{1n} & x_{2n} & \dots & x_{nn} \end{array} \right)$

Tada! Skrivet på ett annat sätt:

$\left(\begin{array}{ccccccccc}B_1 & B_2 & \dots & B_n & | & A_1 & A_2 & \dots & A_n \end{array} \right)$

$\longrightarrow$

$\left(\begin{array}{ccc}I & | & T \end{array} \right)$

där $B_i$ och $A_i$ är kolonnvektor skrivna i standardbasen, $I$ är identitsmatrisen och $T$ är transformationsmatrisen, det vi sökte!

Transformationsmatrisen – del 4

Vi vill göra livet så enkelt som möjligt för oss. Så vi räknar ut transformationsmatrisen som på det andra sättet i Transformationsmatrisen – del 3.

Vi kollar först på ett lite större exempel. Låt oss räkna ut transformationsmatrisen mellan baserna $A$ och $B$ , båda i 5 dimensioner. Säg att vi av någon anledning vet vad vektorerna $A_1, A_2, A_3, A_4$ och $A_5$ har för koordinater i basen $B$ :

$A_1=\left(\begin{array}{c}1 \\2 \\3 \\4 \\5\end{array} \right)_B$

$A_2=\left(\begin{array}{c}-1 \\-1 \\-1 \\-1 \\-1\end{array} \right)_B$

$A_3=\left(\begin{array}{c}0 \\0 \\0 \\0 \\1\end{array} \right)_B$

$A_4=\left(\begin{array}{c}1/2 \\1/2 \\0 \\0 \\0\end{array} \right)_B$

$A_5=\left(\begin{array}{c}5 \\2 \\2 \\2 \\5\end{array} \right)_B$

Och förstås vet vi dem i basen $A$ :

$A_1=\left(\begin{array}{c}1 \\0 \\0 \\0 \\0\end{array} \right)_A$

$A_2=\left(\begin{array}{c}0 \\1 \\0 \\0 \\0\end{array} \right)_A$

$A_3=\left(\begin{array}{c}0 \\0 \\1 \\0 \\0\end{array} \right)_A$

$A_4=\left(\begin{array}{c}0 \\0 \\0 \\1 \\0\end{array} \right)_A$

$A_5=\left(\begin{array}{c}0 \\0 \\0 \\0 \\1\end{array} \right)_A$

Vi betecknar transformationsmatrisen från bas $A$ till bas $B$ med $T$ så länge. Som vanligt får vi uppställningen:

$T\left(\begin{array}{c}1 \\0 \\0 \\0 \\0\end{array} \right)=\left(\begin{array}{c}1 \\2 \\3 \\4 \\5\end{array} \right)$

$T\left(\begin{array}{c}0 \\1 \\0 \\0 \\0\end{array} \right)=\left(\begin{array}{c}-1 \\-1 \\-1 \\-1 \\-1\end{array} \right)$

$T\left(\begin{array}{c}0 \\0 \\1 \\0 \\0\end{array} \right)=\left(\begin{array}{c}0 \\0 \\0 \\0 \\1\end{array} \right)$

$T\left(\begin{array}{c}0 \\0 \\0 \\1 \\0\end{array} \right)=\left(\begin{array}{c}1/2 \\1/2 \\0 \\0 \\0\end{array} \right)$

$T\left(\begin{array}{c}0 \\0 \\0 \\0 \\1\end{array} \right)=\left(\begin{array}{c}5 \\2 \\2 \\2 \\5\end{array} \right)$

T är en 5×5-matris. Om vi tittar noga på första multiplikationen $T\left(\begin{array}{c}1 \\0 \\0 \\0 \\0\end{array} \right)=\left(\begin{array}{c}1 \\2 \\3 \\4 \\5\end{array} \right)$ ser vi att det är nödvändigt att matrisen har $\left(\begin{array}{c}1 \\2 \\3 \\4 \\5\end{array} \right)$ som första kolonn.

På samma sätt följer de andra kolonnerna från de senare ekvationerna.

Alltså:
$T=\left(\begin{array}{ccccc}1 & -1 & 0 & 1/2 & 5 \\2 & -1 & 0 & 1/2 & 2\\3 & -1 & 0 & 0 & 2\\4 & -1 & 0 & 0 & 2\\5 & -1 & 1 & 0 & 5\end{array} \right)$

Eller, om vi kastar en blick tillbaka, så inser vi att de specifika siffrorna inte spelar någon större roll:
$T=\left(\begin{array}{ccccc}[A_1]_B & [A_2]_B & [A_3]_B & [A_4]_B & [A_5]_B\\\end{array} \right)$

med vilket menas att kolonnerna i matrisen är alla de vektorerna $A_1, A_2, A_3, A_4$ och $A_5$ uttryckta i basen $B$ .

Och det är precis vad vi behöver i det generella fallet.

För att bestämma transformationsmatrisen från bas $A$ till bas $B$ , uttryck basvektorerna i basen $B$ och skriv in resultaten som kolonner i en matris.

Riktigt så enkelt är det ju inte, den informationen som krävs har vi inte alltid från början. För att få veta hur man gör i ett jättegenerellt fall, kolla på nästa del.

Transformationsmatrisen – del 3

Det här är fortsättningen på inläggen Transformationsmatrisen – del 1 och Transformationsmatrisen – del 2. I de två första delarna behandlades begreppen bas och vektorernas koordinater i olika baser.

Hur bestämmer man en transformationsmatris?

För att bestämma en matris, vilken som helst matris, är det ett nyttigt första steg att ta reda på matrisens storlek. Det vill säga hur många rader och kolonner den borde ha.

En mxn-matris är en matris med m rader och n kolonner. När en matrismultiplikation sker, händer följande med storlekarna:

mxn-matris gånger nxk-matris resulterar i en mxk-matris

Som ni ser äts det mittersta talet (n) upp, och de andra två kvarstår (m och k) och ger stoleken på resultatmatrisen.

I vårt fall känner vi inte till storleken på vänstraster matrisen (som ska bli transformationsmatrisen), men på de andra två (de är vektorer, kolonnvektorer, som är då kx1-matriser). De är, eftersom vi är i 2 dimensioner, 2×1 matriser.

Alltså: mxn matris gånger 2×1-matris resulterar i en 2×1-matris. Hmm, den siffran som äts upp är i alla fall 2, det vill säga n=2. Och m ska vara samma som den första siffran i resultat, så också 2.

Vi söker en 2×2-matris och en dum men ofta fungerande lösning är att köra brute force, det vill säga ansätta
Transformationsmatrisen= $\left(\begin{array}{cc}a &b\\c &f\end{array} \right)$

Nu ska vi faktiskt minnas vad det var vi höll på med från början. Vi ville bestämma en matris som omvandlade vektorer från standardbasen till bas d.

Det ska alltså bland annat funka för själva basvektorerna.

Ett sätt

Som exempel kan vi välja standardbasvektorer, men jag väljer basvektorerna i basen d. Orsaken är att vi känner till koordinaterna för dem både i bas d, nämligen $d_1=\left(\begin{array}{c}1 \\0\end{array} \right)_d, d_2=\left(\begin{array}{c}0 \\1\end{array} \right)_d$ och i standardbasen, nämligen $d_1=\left(\begin{array}{c}1 \\-1\end{array} \right), d_2=\left(\begin{array}{c}1 \\1\end{array} \right)$ .

Vi kan då ställa upp:
$\left(\begin{array}{cc}a &b\\c &f\end{array} \right) \cdot \left(\begin{array}{c}1 \\-1\end{array} \right)$ blir $\left(\begin{array}{c}1 \\0\end{array} \right)$
samt
$\left(\begin{array}{cc}a &b\\c &f\end{array} \right) \cdot \left(\begin{array}{c}1 \\1\end{array} \right)$ blir $\left(\begin{array}{c}0 \\1\end{array} \right)$

Och utförande matrismultiplikation som vanligt, även om a, b, c och f är okända, får vi:
a-b=1
c-f=0
a+b=0
c+f=1

Det ekvationssystemet kan vi lösa för hand: addera ekvationerna med a och b ledvis, då får vi 2a=1, så a=½, b=-½. På liknande sätt c=½, f=½.

Så transformationsmatrisen= $\left(\begin{array}{cc}1/2 &-1/2\\1/2 &1/2\end{array} \right)$ .

Men man kan göra samma uppgift på flera olika sätt, detta glöms alldeles för ofta när man läser matematik.

Ett annat sätt

Vad händer till exempel om vi istället väljer standardbasvektorerna? De är vektorerna $\left(\begin{array}{c}1 \\0\end{array} \right)$ och $\left(\begin{array}{c}0 \\1\end{array} \right)$ i standardbasen, men vad är de i bas d? Vi kan gissa det eller räkna ut det, ett arbete som kommer löna sig ska det visa sig.
$\left(\begin{array}{c}1 \\0\end{array} \right)=xd_1+yd_2$
$\left(\begin{array}{c}1 \\0\end{array} \right)=x\left(\begin{array}{c}1 \\-1\end{array} \right)+y\left(\begin{array}{c}1 \\1\end{array} \right)$

vilket ger ekvationssystemet x+y=1, -x+y=0 (det liknar lite det vi fick i del 2), som i sin tur ger oss 2y=1 och således y=½, x=½ . På liknande sätt med andra standardbasvektorn:

$\left(\begin{array}{c}0 \\1\end{array} \right)=zd_1+wd_2$
$\left(\begin{array}{c}0 \\1\end{array} \right)=z\left(\begin{array}{c}1 \\-1\end{array} \right)+w\left(\begin{array}{c}1 \\1\end{array} \right)$ som ger ekvationssystemet z+w=0, -z+w=1, som ger 2w=1 och således w=½, z=-½ .
Bekanta tal, eller hur?

Vi har alltså $\left(\begin{array}{c}1 \\0\end{array} \right)_{st}=\left(\begin{array}{c}1/2 \\1/2\end{array} \right)_d$ och $\left(\begin{array}{c}0 \\1\end{array} \right)_{st}=\left(\begin{array}{c}-1/2 \\1/2\end{array} \right)_d$

Vad är då belöningen för denna möda?
Jo, om vi nu ställer upp matrisekvationen precis som innan, fast med nya vektorer, ser vi följande:
$\left(\begin{array}{cc}a &b\\c &f\end{array} \right) \cdot \left(\begin{array}{c}1 \\0\end{array} \right)$ blir $\left(\begin{array}{c}1/2 \\1/2\end{array} \right)$

$\left(\begin{array}{cc}a &b\\c &f\end{array} \right) \cdot \left(\begin{array}{c}0 \\1\end{array} \right)$ blir $\left(\begin{array}{c}-1/2\\1/2\end{array} \right)$

Och utför man matrismultiplikationen med variablerna får man:
a+0=½
c+0=½
0+b=-½
0+f=½

Praktiskt, eller hur? Utan mycket extra möda får vi igen $\left(\begin{array}{cc}a & b\\c & f\end{array} \right)=\left(\begin{array}{cc}1/2 &-1/2\\1/2 &1/2\end{array} \right)$

Det är just den här andra metoden man i allmänhet använder för att ta reda på transformationsmatriser generellt. Vi tittar på ett lite mer generellt fall i nästa del.

Transformationsmatrisen – del 2

Det här är fortsättningen på inlägget Transformationsmatrisen – del 1. I första delen behandlas begreppet baser.

Vektorer i olika baser

Vektorer som skrivs med hjälp av siffror till exempel så här $\left(\begin{array}{c}\sqrt{2} \\5\end{array} \right)$ betyder egentligen ingenting särskilt av sig själv, utan måste ha en bas hängande efter sig som en svans. $\left(\begin{array}{c}\sqrt{2} \\5\end{array} \right)_b$ betyder att en vektor är uttryckt i basen b.

Ofta skriver man inte ut denna svans och det är när man har koll på vilken bas det är som gäller. Ganska ofta menar man standardbasen. Men skriv alltid ut den när det händer basbyten och liknande grejer! Det är lätt att tappa bort sig.

Till exempel är $\left(\begin{array}{c}1 \\2\end{array} \right)_b$ , $\left(\begin{array}{c}1 \\2\end{array} \right)_c$ och $\left(\begin{array}{c}1 \\2\end{array} \right)_d$ helt olika vektorer:

Hur visste jag hur de olika vektorerna såg ut? Jo, $\left(\begin{array}{c}1 \\2\end{array} \right)$ i bas b betyder $b_1+2b_2$ och på samma sätt $\left(\begin{array}{c}1 \\2\end{array} \right)$ i bas c betyder $c_1+2c_2$ och $\left(\begin{array}{c}1 \\2\end{array} \right)$ i bas d betyder $d_1+2d_2$ :

Det vi vill nu är tvärtom: att skriva samma fysiska vektor i olika baser b, c, d. Då kommer dess siffror att se ut på olika sätt.

Exempelvis är vektorn $\left(\begin{array}{c}-1 \\2\end{array} \right)$ i standardbasen lika med:
$v=\left(\begin{array}{c}-1 \\2\end{array} \right)=\left(\begin{array}{c}-1/2 \\1\end{array} \right)_b=\left(\begin{array}{c}-1 \\1\end{array} \right)_c=\left(\begin{array}{c}-3/2 \\1/2\end{array} \right)_d$

Och hur får man tag på dem siffrorna? Jo, man kan antingen ”se” hur många basvektorer av varje sort som behövs för att få vektorn $v$ :

Eller så kan man ställa upp en ekvation, som för basen d. Säg att det behövs $x$ stycken första basvektorer och $y$ stycken andra basvektorer (kan också vara icke-helt antal stycken).

Så $v=x\cdot d_1+y\cdot d_2$ och då
$v=x\cdot \left(\begin{array}{c}1 \\-1\end{array} \right)+y\cdot \left(\begin{array}{c}1 \\1\end{array} \right)$
$\left(\begin{array}{c}-1 \\2\end{array} \right)=\left(\begin{array}{c}x \\-x\end{array} \right)+\left(\begin{array}{c}y \\y\end{array} \right)$
$\left(\begin{array}{c}-1 \\2\end{array} \right)=\left(\begin{array}{c}x+y \\-x+y\end{array} \right)$
De motsvarande koordinaterna skall vara lika, så $-1=x+y$ och $2=-x+y$ . Då har vi att $1=2y$ genom att summera båda ekvationerna ledvis och då måste $y=1/2$ och följaktigen $x=-3/2$ .

Om vi nu behöver göra detta många gånger till (bestämma koordinater med hjälp av ekvationssystem) blir det tröttsamt i längden. I stället kan vi bestämma transformationsmatrisen mellan standardbasen och basen d exempelvis och därefter bara behöva multiplicera med den matrisen.

Jag kan avslöja redan nu att transformationsmatrisen, som tar vektorer i standardbasen och sedan uttrycker dem i bas d är $\left(\begin{array}{cc}1/2 & -1/2\\1/2 & 1/2\end{array} \right)$

Vi testar:
$\left(\begin{array}{cc}1/2 & -1/2\\1/2 & 1/2\end{array} \right) \cdot \left(\begin{array}{c}-1 \\2\end{array} \right)$ blir $\left(\begin{array}{c}-3/2 \\1/2\end{array} \right)$ . Hurra!

Hur man bestämmer sådana här transformationsmatriser kommer att avslöjas i nästa del!