I staden Bilköping finns en parkering med plats för 7×7 bilar. Man kan komma in endast genom porten, resten av parkeringsplatsen är omsluten med staket. En vakt vill parkera så många bilar som möjligt, men så att varje bil kan komma ut samtidigt som alla de andra står stilla. På bilden lyckades han göra så med 24 bilar.
Gåtan är tagen ur en rysk mattetävling för högstadiet, som heter ”Matematicheskij Prazdnik”, vilket översätts ungefär som ”Mattefirande”. De ryska problemkonstruktörerna lyckades som mest med 28 bilar, men huruvida det går med fler är ett öppet problem än så länge. Här är ett exempel på 28 bilar:
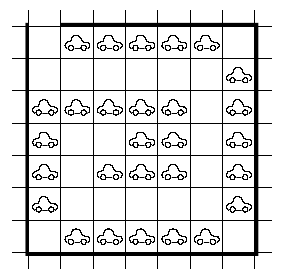
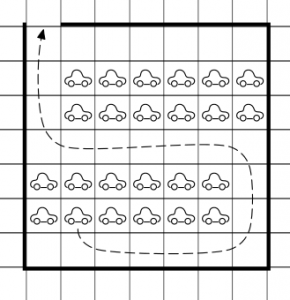
Dock har jag fått höra beviset för varför det inte går med 33 bilar eller fler. Vi tittar på ”vägen”, det vill säga de rutorna, där bilar kan köra ut. Vägen startar från portens parkeringsplats och sedan slingrar sig på något sätt och kan även grena sig.
I vilket fall kan varje vägruta vara utkörningsplats för 1, 2 eller 3 bilar. Men den är det för 3 bilar endast om det är en ”slutruta”. Det kan finnas flera slutrutor, men notera att vägen då måste grena sig och då tjänar vi inte på att ha flera slutrutor (eller snarare: vi tjänar lika mycket på att ha flera slutrutor som att ha en). Till exempel om två slutrutor bidrar med 3 bilar var, så bidrar förgreningsrutan med bara 1 bil max. Därför tänker vi att vi ha en slutruta. Resten av rutorna kan ge plats åt 2 bilar max, förutom den första och den andra rutan, som går längs väggen och därför bidrar med 1 bil var maximalt.
Så ponera att vi har fixat 33 bilar. Då finns 49-33=16 vägrutor. Men de ger plats åt 1×3 + 13×2 + 2×1 = 31 bilar max. Så det går inte.


Hm… Jag lyckas få ut 28 bilar på flera sätt, men det borde gå bättre…
Hittills 32…
28 lyckades mina nior med
Då kommer de med på high score-listan! För övrigt har Johan lyckats bevisa att det inte går med 33 bilar eller fler.
27 hittills…..:)
Vi fick 27 st:(