Bra att känna till:
Det aritmetiska medelvärdet (AM) av två tal 
och 
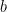är talet 
. Man brukar också bara säga ”medelvärde” om det aritmetiska medelvärdet.
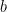Det geometriska medelvärdet (GM) av två tal och är talet 
.
AM-GM-olikheten: Det aritmetiska medelvärdet är alltid större än eller lika med det geometriska medelvärdet för två tal:
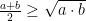
Lösning:
Adam vet att det finns två tal, vars geometriska medelvärde är lika med det andra talparets aritmetiska medelvärde. Hitta en sådan uppdelning av de fyra talen i par, så att det villkoret är uppfyllt. Det vill säga vi har hittat a, b, c, d sådana att
.
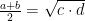Men är de talen verkligen vad vi tror att de är? Det vill säga, måste det vara så att a och b är x+y och x-y (i någon ordning) och c och d motsvarar xy och x/y (också i någon ordning)?
Vi skall visa att det verkligen måste vara så.
Antag att x+y och x-y inte gömmer sig på samma sida om likheten
.
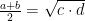Det vill säga, man har tagit likheten
och bytt plats på en av termerna i vänsterledet med en av termerna i högerledet och det ändå blev lika.
Men sådant händer bara om talen vi bytte plats på är lika (annars skulle resultatet på ena ledet minska och på den andra öka, och då skulle de inte varit lika längre).
Och om talen ändå varit lika, så spelar det ingen roll, vilket av dem vi väljer som a (eller b).
Så hur vet vi att a och b är paret 
och inte paret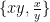 
? Enda sättet att blanda ihop det hela om följande likhet också gäller:
.
Men tillämpa då AM-GM-olikheten:
.
Således får vi:
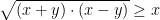
och
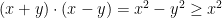
vilket är omöjligt för positiva tal x och y.
Vi vet alltså att ena talet i paret a, b är x-y (nämligen det minsta av dem) och andra är x+y (det största av dem).
Man kan räkna ut x genom att ta (det aritmetiska) medelvärdet av de talen och man räknar sedan ut y, genom att ta det största talet utav a och b och subtrahera x.
