Lösning:
Detta kan vi egentligen räkna ut med vilja, våld och vaselin och sedan se vilket som är större. Men det är lättare att göra beräkningen bakvänd, nämligen införa variabeln x!
I några tävlingsproblem funkar ersättning med variabel jättebra, det förenklar problemet. Låt oss säga att 400=x (man kan också säga att x=400, men det är inte åt det hållet vi arbetar :) ) och då är 399=x-1 till exempel. Allt skrivs om till:
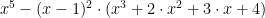
och
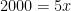
Vi räknar lite på det första polynomet och kollar hur det kan förenklas:
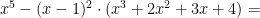
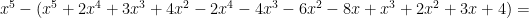
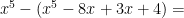
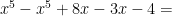
Men är alltid mindre än 
, oavsett vad 
är för någonting! Genom att göra uttrycket mer allmänt gjorde vi jämförelsen lättare.
Således är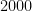 
större än 
.
eller