Skicka in lösningsförslag genom att klicka på länken under uppgifterna senast måndagen den 21 mars. Glöm inte att kolla reglerna och aktuella poängställningen.
Blommor (2 poäng). Längs med vägen mellan Kalles och Kajsas stugor växte blommor på rad: 15 prästkragar och 15 tussilago huller om buller. När Kajsa var på väg till Kalle, vattnade hon alla blommor i rad. Men efter den 10:e tussilagon tog vattnet slut och 10 blommor förblev ovattnade.
Nästa dag gick Kalle hem till Kajsa och plockade blommorna i rad. Efter den 6:e tussilagon tyckte han att buketten var lagom stor. Hur många blommor fick växa kvar längs med vägen?
Familjealbum (5 poäng). I ett familjealbum finns 10 foton. Varje foto föreställer tre personer: i mitten står en man, på hans vänstra sida har han sin son och på hans högra sida har han sin bror.
Alla männen som står i mitten är olika personer. Vilket är det minsta antalet olika människor som kan finnas på bilderna i albumet?
Visa lösningar
Blommor (Daniels lösning):
Eftersom det sammanlagt finns 30 blommor (15+15) och efter den 10:e tussilagon så finns det 10 blommor kvar på raden. Kvar finns där 5 tussilagos och 5 prästkragar på raden. När Kalle plockar den 6:e tussilagon från andra hållet så blir det alltså samma tussilago som den 10:e från Kajsas håll.
De tio blommorna som är kvar efter den 10:e från Kajsas håll + den tionde tussilagon blir 10+1=11 blommor i buketten och 30-11=19 blommor kvar på raden.
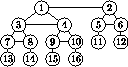
Familjealbum (Johans lösning): Vi kan anta att på varje bild så är sonen den äldste sonen, och brodern den ”ett steg yngre” brodern (där den ett steg yngre bordern till den yngsta brodern i en grupp är det äldsta syskonet). Vi kan också anta att för varje broderssyskonskara som är med så är alltid det äldsta syskonet med som fader på något foto.
Antag att det går att skapa ett sådant familjealbum med endast 15 personer. På varje foto förekommer 2 typer av ”relationer”, nämligen X är äldste sonen till Y och X är ett steg yngre brodern till Y. Mellan två personer X, Y så kan endast en av dessa relationer försigkomma. Totalt så har vi 20 relationer i bilden.
Vi ritar en graf med de 15 personerna som noder och vi bildar kanter där vi har en relation (vi kan anta att grafen är sammanhängande). Ifall vi inte ritar ut relationerna där den äldste brodern anses ett steg yngre än den yngste så har vi en riktad graf utan loopar, dvs ett träd. Ett träd med 15 noder har 14 kanter.
Vi behöver alltså 6 relationer till. Dessa kan nu bara komma från yngste->äldste brodersrelationer, och vi kan bara få en sådan från varje syskongrupp. Vi måste alltså ha minst 6 syskongrupper, där varje person i syskongruppen är avbildad som fader på något foto (pga relationsegenskapen). En sådan grupp måste bestå av minst 2 personer. Då har vi minst 12 personer som är fäder på något foto. Detta motsäger att vi har 10 foton.
Här är exempel på ett släktträd med 16 män: