En ny termin är igång och för mig innebär det söndagsträffar med mina matematiksugna 5-, 6-, 7- och 10-åringar! Förra terminen skrev jag om våra 6 träffar, men vi har egentligen haft 11 stycken och i vår ska vi ha ungefär lika många!
Gamla träffar:
Träff 1 och 2
Träff 3 och 4
Träff 5 och 6
Den här våren tänkte jag prova att ha 1-2 övergripande teman på varje lektion, ungefär samma tema för stora som för små barn. Uppgifterna kommer dock variera för olika åldrar. De planerade aktiviteterna ska jag försöka lägga upp här på bloggen i förväg, så ni kan komma med synpunkter och förslag. De riktiga lektionerna blir aldrig i och för sig exakt som planerat, men i alla fall hälften av aktiviteterna hinns med (det gäller att ha aktiviteter med sig med marginal!).
Vinklar
Vi har nämnt vinklar och hörn lite grann förra terminen och svarat på frågor av typen:
– Hur många hörn har rummet? (Svaret var 6 för vårt rum)
– Hur många hörn har bordet? (Svar: 4)
– Bordet består egentligen av två mindre. Hur många hörn blir det om man förskjuter ena halvan? (Svar: 8, eftersom vinklar som är större än 
Här är en kortfattad plan på hur jag ska lägga upp lektionen för barnen (där det inte står något, utgå från att de är 5-7 år gamla):
Introduktion till matematiska begrepp
Jag berättar om spetsiga, räta och trubbiga vinklar, visar exempel och ber dem att hitta olika sorts vinklar i rummet. Finns det andra vinklar än räta i verkligheten? Ja, men man får leta efter dem lite längre (ett exempel är klockans visare).
Lek med vinkelexempel
Barnen får dra kort, ett i taget, och säga vad för sorts vinkel det är på bilden (trubbig, spetsig, rät). Man måste visa att man har rätt också och det kan man göra genom att lägga vinkel inuti en rät t.ex., för att visa att den är spetsig. Sådant kommer jag be om, när en vinkel är väldigt nära en rät, så det är svårt att avgöra vinkelns sort. Jag frågar efteråt om det finns vinklar som är lika stora och även då får barnen bevisa sina hypoteser genom att t.ex. lägga vinklarna på varandra.
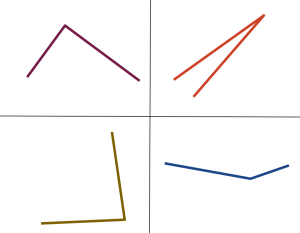
Bara den färgade delen (själva vinklarna) ska lamineras för att uppgiften ska gå att genomföra som planerat.
Färga vinklar
För att associera även det inre med ordet ”vinkel” (se bilden nedan), ska vi måla lite (barn älskar att måla!) och samtidigt träna lite kombinatorik.
Hur många vinklar ser du på bilden? Måla alla möjliga vinklar i olika färger (det finns 6 stycken mindre än 180 grader och barnen får 6 uppsättningar av bilden):
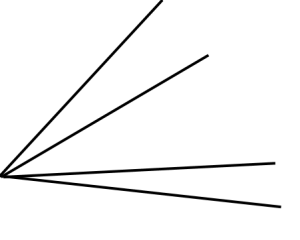
Rita egna vinklar
Barnen ritar några egna vinklar. Vissa får i uppgift att rita spetsiga, vissa trubbiga och vissa räta.
Nästa uppgift är att rita två linjer som skär varandra och räkna antalet spetsiga samt trubbiga vinklar på bilden.
Bygga ihop 
Jag har med ett pusselspel, som egentligen är menat till att lära sig bråk. Det är cirkelsektorer i plast i olika färger som är lika stora som 1/3 av cirkeln eller 1/8 till exempel. Sektorer av samma storlek har samma färg, till exempel är alla tredjedelar gula, alla åttondedelar – gröna.
Plastbitarna presenterar jag som vinklar. Barnens uppgift är att bygga ihop en cirkel utan ”vinklar” som inte alla har samma färg. Till exempel, ![\frac{1}{2}+\frac{1}{3}+\frac{1}{6}\](http://l.wordpress.com/latex.php?latex=%5Cfrac%7B1%7D%7B2%7D%2B%5Cfrac%7B1%7D%7B3%7D%2B%5Cfrac%7B1%7D%7B6%7D%5C%20&bg=FFFFFF&fg=000000&s=0 "\frac{1}{2}+\frac{1}{3}+\frac{1}{6}\")
![\ 180^\circ+120^\circ+60^\circ=360^\circ\](http://l.wordpress.com/latex.php?latex=%5C%20180%5E%5Ccirc%2B120%5E%5Ccirc%2B60%5E%5Ccirc%3D360%5E%5Ccirc%5C%20&bg=FFFFFF&fg=000000&s=0 "\ 180^\circ+120^\circ+60^\circ=360^\circ\")
Dessa ”tårtbitar” återvänder vi till när vi ska prata om bråk.
De äldre barnen (10 år) får göra samma uppgift, men de måste mäta vinklarna med gradskiva och lägga ihop siffrorna, för att komma fram till att summan är 360 grader om vinklarna tillsammans bildar en cirkel.
Andra experiment för de äldre är att rita trianglar, riva bort hörnen och mäta vinkelsumman. Alternativt lägga hörnen bredvid varandra och se att det blir en rät linje (alltså 180 grader). Samma uppgift med fyrhörningar och femhörningar.
Rita en stjärna
Jag visar för de äldre barnen hur man kan rita exakta vinklar med hjälp av en gradskiva. Sedan får de lära sig att rita en femuddig regelbunden stjärna med passare, linjal och gradskiva.
Detta är allt för den första lektionen om vinklar! Notera att jag också hade tänkt med att hinna med ett annat tema, nämligen tal upp till 100 (och med de äldre barnen, delbarhet upp till 100).
Det kanske skulle vara intressant för de äldre barnen att ta med en badboll och rita trianglar på den och undersöka vinkelsummor om det finns tid?
Det låter intressant! Finns det något sätt att fysiskt se vinkelsumman (för att inte behöva mäta med gradskiva och addera för hand)? Jag antar att det inte är så lätt att göra pappersbollar.
Ritar man stora trianglar så är det ganska lätt att se att vinkelsumman inte är 180 (för väldigt små trianglar så är den ”nästan” 180, t.ex om man ritar trianglar på marken så ritar man ju egentligen på en stor sfär). Man kan ganska lätt se att man har 90 grader överallt ifall man tar motsvarande tre av enhetsvektorerna i R^3 som startpunkterna i triangeln (det går ju att fuska och markera ut startpunkterna i förväg om man vill att de ska titta på specifika trianglar), och alltså har en triangel med vinkelsumma 270. Om någon tycker om att mäta för hand så är det en trevlig laboration att ta 3 stycken succesivt mindre liksidiga trianglar och se att att vinklarna minskar (igen så kanske förmärkta mätpunkter är bra). Man kan ju då fundera just på varför små trianglar beter sig mer och mer som om de var ritade på ett plan odyl.
Om man hade mer intresserade/gamla elever kan man fortsätta på ganska många sätt, prata om krökning (kanske tillochmed universums eventuella krökning, som man försöker mäta med trianglar med en rymdsond i varje ”hörn”), klistra ihop modeller av hyperboliska plan gjorda av små trianglar etc. En lite lättare variant är att gå in på klassisk grekisk fysik, om vi nu tror/vet att jordytan inte är platt, hur kan vi mäta jordklotets radie (utan långa måttband)? Det kräver ganska enkel trigonometri, se tillexempel sierra.nmsu.edu/morandi/CourseMaterials/RadiusOfEarth.html
Tack för tipsen Johan!
Mina barn som jag undervisar i grupp (de är 10 år och inte så matteerfarna än) har nog svårt för att ”se” en vinkelsumma på 180 grader (eller mer eller mindre). De behöver mer erfarenhet av trianglarnas vinkelsumma och jag tror att det ger mer förvåningseffekt att göra sfärisk geometri när man van vid den euklidiska varianten. Men de laborativa uppgifterna kommer definitivt passa senare!