Borromeiska trianglar

Ny mellanstadietävling
I Sverige finns en tradion av tävlingar för högstadier (HMT, Pythagoras Quest, Sigma8) och gymnasiet (SMT) men nästa inga tävlingar finns för mellanstadiet!
Vissa skolor anordnar förstås Känguru, men det är en individuell
Varierande problemlösningslektioner

I veckan besökte jag Matematikbiennalen i Karlstad, en stor händelse för mattelärare, där ett par tusen besökare fick vara med om föreläsningar, workshops och utställningar. Allt handlade om matematikundervisning.
Jag höll i en föreläsning där
Jobba efter 80

I januari anordnades en fantastiskt konferens i Piteå med kodnamnet Knuth80. Den berömda matematikern, programmeraren och författaren Donald E. Knuth (skaparen av TeX) fyllde 80 år och hans vänner och familj bestämde sig såklart att anordna en
Korstal 2015

Korstal 2015
Fyll i precis som ett vanligt korsord (men endast med siffror). Obs! Inga tal börjar med noll.
Vågrätt:
1. En tvåpotens (det vill säga 2n).
7. Har samma siffersumma som vågrätt 15.
8. Talet siffersumma är
Kvadrater i trappan
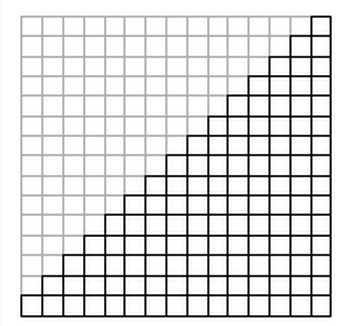
Kvadrater i trappan
Vilket är det minsta antalet kvadrater som man kan klippa upp trappan nedan i? Man får bara klippa längs med rutnätets linjer. (Det är alltså 15 trappsteg i trappan.)
Visa lösningen
Det finns 15 små
Gammaldags klocka
![]()
Gammaldags klocka
En gammaldags klocka slår lika många slag som antalet timmar är när den slår in en ny timme: Till exempel slår den 2 slag om klockan är 2 på dagen eller naten och 12 slag om det är 12 på dagen eller natten.
Dvärgar på en bro
![]()
Dvärgar på en bro
300 dvärgar ska gå över en bro mitt i polarnatten. Bron är ranglig och klarar av som mest två dvärgar i taget. Med sig har de en lykta som de måste ha med vid varje övergång. Dvärgarna behöver olika tid för att gå över bron: 1
Två pjäser på en 12-hörning
![]()
Två pjäser på en 12-hörning
En svart och en vit pjäs står i två intilliggande hörn av en 12-hörning. På ett drag får man flytta en valfri pjäs till ett ledigt grannhörn. Man får inte gör drag som leder till att pjäserna står på ett
Multiplikationer i en tabell
![]()
Multiplikationer i en tabell
På hur många sätt kan man fylla en 6x6-tabell med 1:or och -1:or så att produkten av talen i varje rad och i varje kolumn blir lika med 1? (Det är alltså tolv stycken produkter som ska bli lika med 1.)
Bollförrådet
![]()
Bollförrådet
I förrådet till gympasalen låg fotbollar och volleybollar, lika många bollar av varje sort. Gympaläraren skulle anordna en volleybollturnering, och när han hade tagit ut några volleybollar, så låg det kvar 7 gånger så
Bankuttag
![]()
Bankuttag
På ett bankkonto ligger exakt 500 euro. Det är tillåtet att antingen ta ut 300 euro från kontot eller sätta in 198 euro på kontot. Det finns inga andra pengar än de som ursprungligen ligger på kontot. Hur mycket pengar kan
Kubkonstruktion
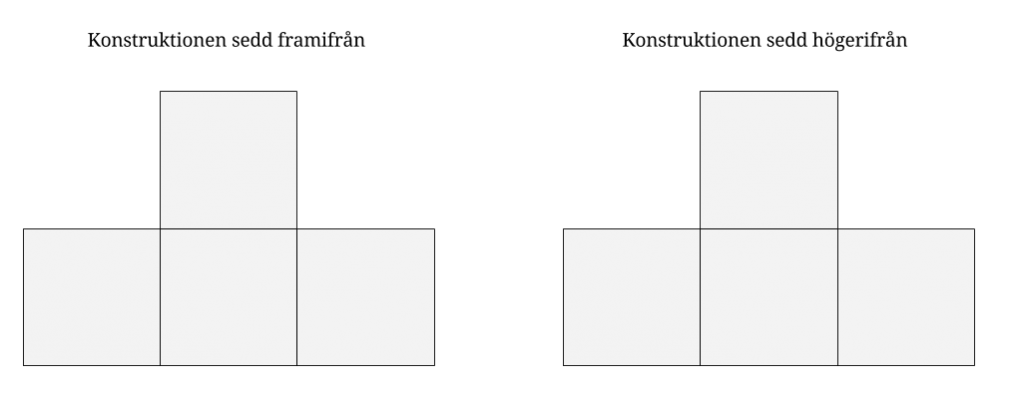
Kubkonstruktion
En konstruktion som är byggd av likadana kuber ser ut på samma sätt både framifrån och högerifrån. Vilket är det minsta antal kuber som konstruktionen kan bestå av? (Konstruktionen följer fysikens
Intressanta tal
![]()
Intressanta tal
Ett femsiffrigt tal kallas för ''intressant'' om alla dess siffror är olika och den första siffran är lika med summan av de övriga. Hur många intressanta femsiffriga tal finns det?
Visa lösningen
Den första
Lykstolpar på gatorna
![]()
Lykstolpar på gatorna
På en gata finns 10 lyktstolpar utplacerade med jämna mellanrum, varav en lyktstolpe finns precis i början av gatan och en finns i slutet.
På samma sätt så finns det 100 lyktstolpar på en annan gata, med
Öriken
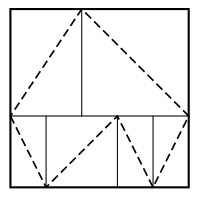
Öriken
Det Stora och det Lilla Riket är båda rektangulära öar och uppdelade i rektangulära landskap. I varje landskap finns en väg som går längs med en av diagonalerna. På varje ö bildar vägarna en sluten rutt, som inte går igenom
Schackturnering
![]()
Schackturnering
Svårare gåta att klura på under helgen!
12 schackspelare deltog i en turnering. Var och en spelade mot var och en av de andra exakt en gång. Efter turneringen gjorde varje schackspelare 12 listor med namn. På den
Bildäck
![]()
Bildäck
Lite svårare gåta att klura på under helgen!
Däcken som sitter fram på bilen slits ut efter 25000 km, medan däcken som sitter bak slits ut efter 15000 km. Hur långt kan man maximalt åka med helt nya däck om man får byta
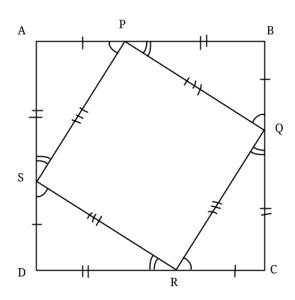
Fyrhörningens diagonal
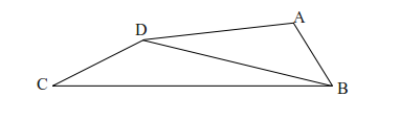
Fyrhörningens diagonal
I fyrhörningen ABCD är AB = 5 cm, BC = 17 cm, CD = 5 cm, DA = 9 cm och sträckan BD är ett helt antal cm. Hur lång är sträckan
Julnötter
![]()
Julnötter
På julmarknaden såldes en försäljare julnötter i en marknadsstånd. Först kom en person och köpte en nöt, nästa kund köpte två nötter, nästa köpte fyra och så vidare, det vill säga varje ny kund köpte dubbelt
Tågpassage
![]()
Tågpassage
Ett tåg som är 180 m långt passerar en lyktstolpe på 9 sekunder. På hur lång tid passerar tåget en bro som är 360 m långt?
Visa lösningen
Vi kan låtsas som att vi sätter ut tre lyktstolpar på bron:
Tentor
![]()
Tentor
En student skrev totalt 31 tentor under de fem åren hon studerade på universitetet. Varje år skrev hon fler tentor än det föregående året och det sista året skrev hon tre gånger så många tentor som första året.
Djur på vägen
![]()
Djur på vägen
På en väg fanns lika många grisar, ankor och kycklingar. Totalt hade de 32 fötter. Hur många ankor fanns på vägen?
Visa lösningen
Ett gäng på en gris, en anka och en kyckling har 4+2+2 = 8
Jämn siffra efter udda
![]()
Jämn siffra efter udda
Vanda skrev talen från och med 1000 till och med 2000 i ordning på en rad som ett enda långt tal:
1000100110021003....19992000
Hur många gånger skrev hon en jämn siffra direkt efter en udda
Bussar på vägen
![]()
Bussar på vägen
Lars går längs med en väg med konstant hastighet. Var 6:e minut ser han en buss som åker förbi honom och var 3:e minut möter han en buss som åker åt andra hållet. Bussarna åker med samma fart åt båda håll och startar
Ihoplimmad kub
![]()
Ihoplimmad kub
Av 27 kuber av storleken 1x1x1 limmade man ihop en kub av storleken 3x3x3 genom att alla kontaktytor limmades. För att limma ihop två sidor använde en droppe lim varje gång. Hur många droppar lim använde man totalt?
Skolsteg
![]()
Skolsteg
Maria, Jakob och deras pappa går till skolan tillsammans. Under tiden som pappa tar 3 steg, så tar Maria 5 steg. Under tiden som Maria tar 3 steg, så tar Jakob 5 steg. Maria och Jakob räknade till att de tog 400 steg till
Glassbekymmer
![]()
Glassbekymmer
Valentina ville köpa en glass, men saknade 7 kronor. Robert ville köpa samma sorts glass, men saknade 1 krona. Då bestämde de sig för att lägga ihop sina pengar, men även då räckte de inte för att köpa en sådan
Matematik i Genikampen – fjärde och femte avsnittet

Första, andra och tredje avsnittet av Genikampen innehöll en hel del matte, medan avsnitt fyra och fem var mycker mer fysikinriktade. Jag har inte så bra förståelse för fysik, så jag ska försöka framlägga hur jag försökte göra mitt bästa genom att
100-våningshuset

Tack till David Nilsson som påminnt mig om en gammal klassiker!
Rekommenderad från: 13 år
En apa är i ett 100-våningshus och vill veta vilken den högsta våningen är som den kan släppa en kokosnöt ifrån utan att den går sönder när det träffar
Matematik i Genikampen – tredje avsnittet

Tredje avsnittet av Genikampen innehöll mycket matte! Så mycket att det inte hanns med att skriva om det innan avsnitt fyra kom ut. Avsnitt fyra och fem kommer jag däremot att slå ihop till ett inlägg.
Avsnitt tre innehöll tre tävlingar:
Matematik i Genikampen – kluringar från tredje avsnittet
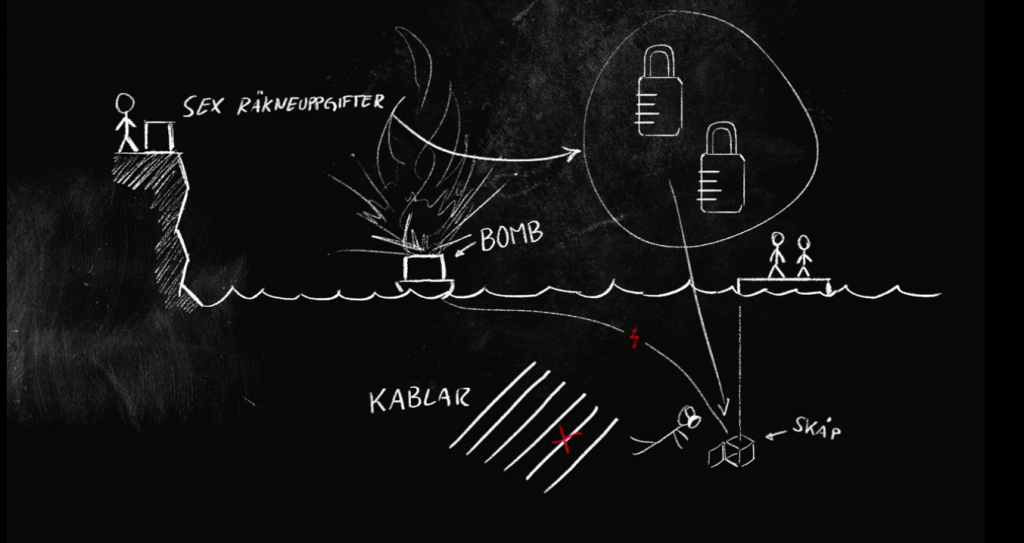
Det tredje avsnittet av Genikampen var sprängfyllt med matte! Det var så pass mycket matte att jag behöver dela upp inlägget om det i två delar. I första delen vill jag presentera problemen som ingick i den andra lagtävlingen, samt lösningar till de
Matematik i Genikampen – andra avsnittet
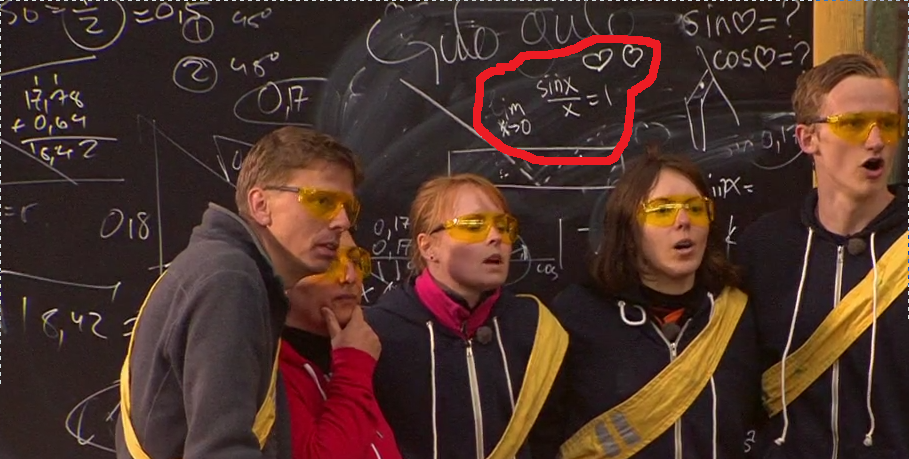
Andra avsnittet innehöll kanske inte lika mycket matte som första avsnittet, men det betyder ju inte att man inte skulle vara smart för att klara tävlingarna. Och allt som har med kreativt tänkande att göra kan jag om jag vill koppla ihop med matte
Matematik i Genikampen - första avsnittet
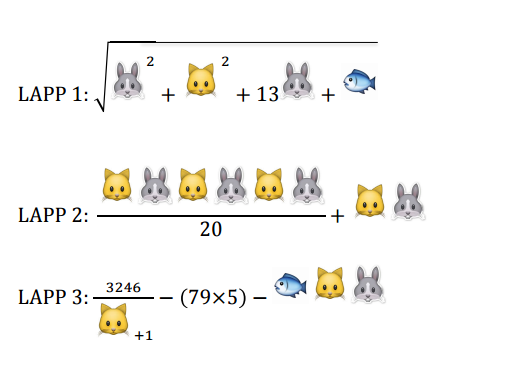
I höst är jag en av deltagarna i SVT:s program Genikampen. Programmet går i åtta avsnitt och jag tänkte beskriva händelserna i avsnitten ur ett matematiskt perspektiv.
Själv är jag matteintresserad och har övat mycket i problemlösning. Jag tror
Tre vinklar
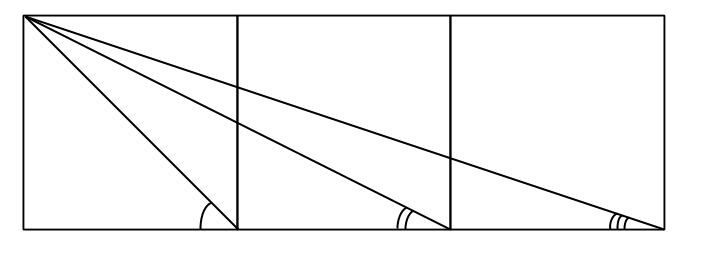
Det här roliga problemet har jag fått av min kompis Fredrik från Genikampen-2015!
Rekommenderad från: 15 år
Tre kvadrater är ritade bredvid varandra. Tre linjer dras från ett hörn som bilden visar. Bestäm summan av de tre utsatta vinklarna (i
Mattekollo 2015
![]()
Vad är Mattekollo?
Mattekoll 2015 är ett dagsläger för elever i åk 6-7. Lägret kommer att hållas 3-13 augusti på Ångströmlaboratoriet i Uppsala, och elever från hela Sverige är välkomna att delta! Mattekollo riktar sig till elever som är
Mynten på schackbrädet

Rekommenderad från: 15 år
Du sitter i en fängelsehåla och en vakt kommer till dig med ett erbjudande. Han säger att han kommer lägga upp mynt (totalt 64 st.) på ett schackbräde, ett mynt i varje ruta och det kommer vara slumpat för varje mynt
Spionuppdrag

Rekommenderad från: 12 år
En hemlig byggnad består av många rum som ser exakt likadana ut och som är kopplade i en stor ring med små korridorer. I varje rum finns en lampa och en lampknapp. En spion hamnade i ett av rummen. Hur ska han bestämma
Min vision av Mattekollo 2015

Det är riktigt kul att höra att så många är positiva till idén att ha Mattekollo nu i sommar! Här tänkte jag skriva lite mer detaljerat om vad jag har för vision.
Var ska det vara?
Då jag själv åkt på kollo som barn vet jag att jag inte bara
Team till Mattekollo sökes
Nästan varje vecka får jag träffa elever som blir glada av mina lektioner. Många av dem går på Matteklubben i Uppsala - kommunens satsning på begåvade elever i matematik. Senast igår fick jag en kommentar om att det "lyser om barnen" som går från
Tändsticksproblem med twist
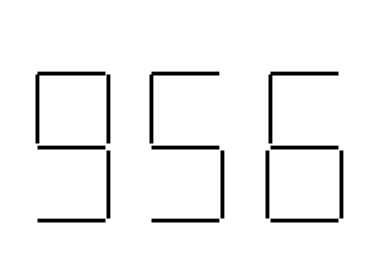
Det finns många tändsticksproblem som går ut på att flytta tändstickor för att få kvar någon särskild figur eller för att en viss likhet ska uppfyllas. Ett exempel på ett sådant problem kan du hitta i tidningen Forskning och Framsteg.
Här är dock
HMT-final 2015

Finalresultat
För en dryg vecka sedan hölls finalen i Högstadiets Matematiktävling i Stockholm! 49 skarpa hjärnor var med och löste 6 matematiska problem på tid och en kom ut som vinnare. Grattis Björn Magnusson från Lund som fick fullpoäng på alla
Fjärde träffen med Matteklubben, åk 7-9
![]()
Du kan läsa om vad som har hänt på de tidigare träffarna här: första träffen, andra träffen och tredje träffen.
Introduktion till informationsteori
Vi började lektionen med leken "Gissa talet". Jag tänkte på ett tal mellan 1 och 10 och
Fjärde träffen med Matteklubben, åk 2-4
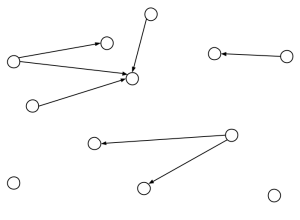
Minsta eleverna som går i Matteklubben är de i åk 2-4. Du kan läsa om första, andra och tredje träffen med gruppen.
Nytt sätt att sitta
Den sista gången för terminen testade vi en ny bordsuppställning. Vanligtvis brukar vi behålla lektionssalen
Fjärde träffen med Matteklubben, åk 5-6
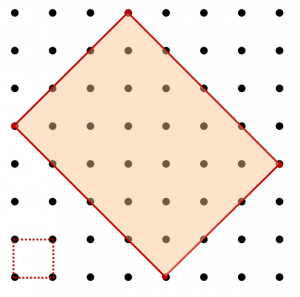
Matteklubben är Uppsala kommuns satsning på begåvade elever i matematik. Jag har äran att förbereda aktiviteterna som vi håller på med och vara en av lärarna. Du kan kolla upp var vi gjorde på första träffen, andra träffen och tredje träffen innan
Korstal 2014

Korstal 2014
Fyll i precis som ett vanligt korsord (men endast med siffror). Obs! Inga tal börjar med noll.
Ladda ner för utskrift
Vågrätt:
1. Delbart med 9
4. Valören på en svensk sedel
5. Alla siffror i talet är
Summan av produkter
![]()
Summan av produkter
För varje tresiffrigt tal skrev man upp produkten av dess siffror. Sedan räknade man ut summan av alla dessa produkter. Vad fick man för tal? (Om en av siffrorna i talet är 0, så är sifferprodukten såklart 0
Månskäran

Månskäran
I hur många delar kan man som mest dela upp månskäran med hjälp av 5 raka linjer? Delarna får inte arrangeras om mellan skärningarna.
Visa lösningen
Månskäran kan delas upp i 21 delar till exempel så som
Bråkdelar
![]()
Bråkdelar
En speciell miniräknare har bara en knapp. Genom att trycka på den ökar man talet på skärmen med dess bråkdel (t.ex. kan man få 6/7 från 3/7 då 3/7 + 3/7 = 6/7 eller 4,6 från 3,8 då 3,8 + 0,8 = 4,6). Från början stod ett
Shejkens slott

Shejkens slott
En shejk har ett slott som ser ut som en 6x6-kvadrat indelad i 1x1-rum. I mitten av varje vägg finns en dörr mellan rummen. Shejken ger order till hovbyggaren att ta bort några väggar, så att det bara bildas rum av
Virusattacker
![]()
Virusattacker
Datorerna med nummer från 1 till 100 är kopplade i en kedja: 1 är kopplad till 2, 2 kopplad till 3, osv., 100 är kopplad till 1. Några hackers har förberett hundra olika virus, som de har gett nummer från 1 till 100
Ett fotbollslag
![]()
Ett fotbollslag
I ett fotbollslag med 11 spelare är genomsnittsåldern 22 år. Under matchen fick en av spelarna en skada och var tvungen att lämna planen. Då blev genomsnittsåldern för spelarna på planen 21 år. Hur gammal var
Synliga rutor

Synliga rutor
På ett rutat papper har man markerat 9 blå rutor så som bilden nedan visar. Från punkten A kan man (helt eller delvis) se 5 av de blå rutorna. Hur många av rutorna kan man som mest se om man får välja en annan punkt
Termometrar
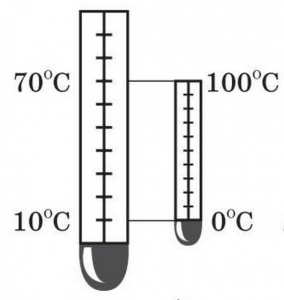
Termometrar
Två kvicksilvertermometrar hänger bredvid varandra så som bilden visar. Vid vilken temperatur kommer kvicksilvret vara på samma höjd i båda termometrarna?
Visa lösningen
60 steg (70-10) på den första
Le Havre till New York
![]()
Le Havre till New York
Varje dag, exakt mitt på dagen, startar en båt med post från Le Havre till New York och samtidigt utgår en båt av samma bolag från New York till Le Havre. Var och en av båtarna åker exakt sju dygn längs med
Åldersjämförelse
![]()
Åldersjämförelse
Om en grupp med fem människor vet man följande:
Nils är 1 år äldre än Nilsson, Sven är 2 år äldre än Svensson, Anders är 3 år äldre än Andersson, Erik är 4 år äldre än Eriksson. Man vet att det finns en Johan och
Luciasånger
![]()
Luciasånger
Fyra pojkar övade på att sjunga luciasånger. På varje sång är det en av dem som spelar piano och de andra tre sjunger. Det visade sig att Johan sjöng flest sånger av alla, sju, medan Simon sjöng minst sånger av alla,
Den magiska fruktgranen
![]()
Den magiska fruktgranen
Om Knatte knackar på den magiska fruktgranen, faller det ner ett äpple och två bananer från den. Om Tjatte knackar på samma fruktgran, så faller det ner ett äpple och två apelsiner (Obs! Stod "bananer"
Brottartävling
![]()
Brottartävling
100 brottare med olika styrkor ställde upp i en tävling. I en match möts två brottare och den starkare vinner alltid över den svagare. Först delade brottarna upp sig i par och körde mot varandra. Sedan delade alla
Kvadrat i kvadrat i kvadrat
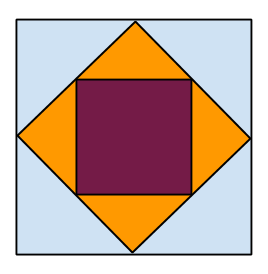
Kvadrat i kvadrat i kvadrat
I en kvadrat med sidan 1 m placerade man en annan kvadrat, vars hörn hamnade precis på mittpunkterna av den första kvadratens sidor. Likadant placerade man den tredje kvadraten inuti den andra. Vilken
Fruktrad
![]()
Fruktrad
På en rad ligger frukter: apelsiner, clementiner, äpplen och päron. Det visade sig att bredvid frukter av en viss sort (och det här gäller för alla sorter) förekommer frukter av alla andra sorter. Vilket är det minsta
Överhällningar
![]()
Överhällningar
På bordet står två behållare med 1 liter vatten i varje. Först häller man över hälften av vattnet från den första behållaren till den andra. Sedan häller man över en tredjedel av vattnet som finns i den andra
Avstånd mellan städer
![]()
Avstånd mellan städer
Från Lingonby till Malort är det 660 km, från Lingonby till Lysekil är det 310 km, Från Lysekil till Kåbo är det 200 km, från Kåbo till Malort är det 150 km. Hur långt är det mellan Malort och
Småkuber
![]()
Småkuber
Man målade hela ytan på en kub och sedan sågade upp den i likadana småkuber. Det visade sig att det fanns småkuber med bara en målad sida och de var lika många som småkuberna som var helt omålade. I hur många småkuber
Ettor och tvåor
![]()
Ettor och tvåor
Vilket är det största talet man kan skriva med hjälp av bara ettor och tvåor som uppfyller följande egenskap: Summan av vilka som helst fem siffror som kommer efter varandra i talet måste vara jämn, medan summan av
Hemligt tal
![]()
Hemligt tal
Julia tänkte på ett tal, multiplicerade sedan det med 13, strök sista siffran i resultatet, sedan multiplicerade det nya talet med 7, återigen strök sista siffran i resultat och då fick hon 21. Vilket tal tänkte Julia på
Bryta chokladkakan
![]()
Bryta chokladkakan
I present får Mats en chokladkaka som har 15 × 6 rutor. Mats bryter en bit (från början utgör chokladkakan den biten) i taget, längs med en av dess skåror. Hur många brytningar måste han göra, för att det bara
Tresiffriga tal
![]()
Tresiffriga tal
Hur många tresiffriga tal har siffran 0 i mitten?
Visa lösningen
Tresiffriga tal som börjar med 1 och har 0 i mitten är 10 stycken, lika många som det finns slutsiffror (alla tio siffror är möjliga som
Språkval
![]()
Språkval
I klassen är det 14 elever som har valt att studera tyska, 8 som valt att studera franska. Det finns 3 elever som valt båda språken. Hur många elever går i klassen om man vet att alla valde åtminstone ett språk?
Visa
Tredje träffen med Matteklubben, åk 7-9
![]()
Du kan läsa om vad som har hänt på de tidigare träffarna här: första träffen och andra träffen.
På grund av hastigt salsbyte rådde lite förvirring i början om var vi skulle hålla hus, men precis till lektionens början kunde vi samlas i en och
Tredje träffen med Matteklubben, åk 2-4
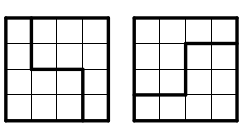
Minsta eleverna som går i Matteklubben är de i åk 2-4. Du kan också läsa om den första träffen och den andra träffen med gruppen.
Från början hade vi tänkt att både ha med en del med blandade problem och en tematisk del. Vi hann dock bara gå
Tredje hemuppgiften från Matteklubben, åk 5-6

Här i kommentarerna kan du diskutera hemuppgiften. Skriv om du har frågor eller förslag på lösning/svar.
• I ett höghus med 100 våningar finns en hiss, som bara har två knappar: ”+7” och ”-9”. Den första knappen får hissen att gå upp sju
Tredje träffen med Matteklubben, åk 5-6
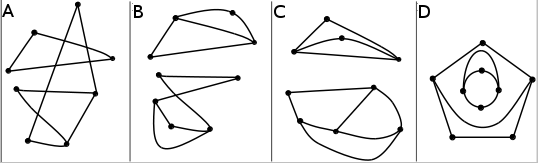
Matteklubben är Uppsala kommuns satsning på begåvade elever i matematik. Jag har äran att förbereda aktiviteterna som vi håller på med och vara en av lärarna. Du kan kolla upp var vi gjorde på första träffen och andra träffen innan du läser
Andra hemuppgiften från Matteklubben, åk 7-9
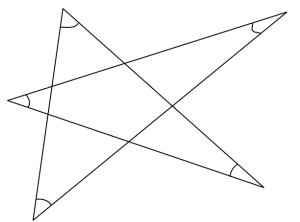
På lektionen bevisade vi att vinkelsumman i en godtycklig triangel är 180° och en i fyrhörning 360°. Hur blir det med en femhörning, sexhörning osv.? Och hur bevisar man resultatet?
Det är inte bara månghörningar som har en viss bestämd
Andra träffen med Matteklubben, åk 7-9
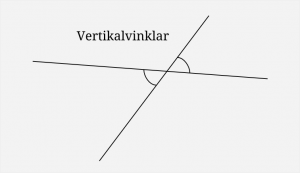
Under andra matteträffen med högstadiet hade vi 19 elever som besökte oss. Vi var 3 lärare plus en till som hjälpte lite grann. Det var alldeles lagom för en grupp med elever som inte så ofta räcker upp handen. Men hade eleverna varit lika aktiva
Andra träffen med Matteklubben, åk 2-4

Minsta eleverna som går i Matteklubben är de i åk 2-4. Du kan också läsa om den första träffen med gruppen här på bloggen.
På den andra träffen kom färre elever, men de var precis lagom många för att vi skulle hinna prata med alla. Barn i
Andra hemuppgiften från Matteklubben, åk 5-6
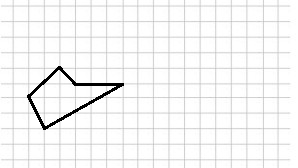
Här i kommentarerna kan du diskutera hemuppgiften. Skriv om du har frågor eller förslag på lösning/svar.
• En viss figur hade arean 12 cm2. Om den figuren förminskas så att alla dess sidor bli hälften så stora, vad kommer dess area att bli
Andra träffen med Matteklubben, åk 5-6
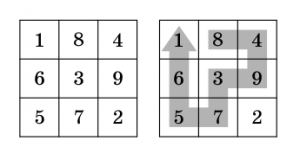
Matteklubben är Uppsala kommuns satsning på begåvade elever i matematik. Jag har äran att förbereda aktiviteterna som vi håller på med och vara en av lärarna. Du kan kolla upp var vi gjorde på första träffen innan du läser vidare.
36 elever och 6
Vetenskapstävlingar
![]()
När man lär sig vissa skills så finns det ofta sätt att utvärdera dem. I karate finns det bälten av olika färger som visar på vilken nivå du har uppnått hittills. Om du lär dig att dansa så ordnas det dansföreställningar som markerar slutet av någon
Delbart med 2014

Rekommenderad från: 13 år
[kkratings]
Visa att man kan stryka några siffror i början och några i slutet av talet
(talet består av 2000 siffror), så att summan av de resterande siffrorna blir delbart med 2014.
Visa lösningen
Om
Lösningar till SMT-kvalet 2014
Detta är de inofficiella (dagen-efter) lösningar till SMT-kvalet som hölls den 30:e september på gymnasieskolorna över hela Sverige. De officiella lösningarna kommer att komma upp på SMT:s hemsida.
Problem 1
Ett tåg kör fram och tillbaka
Första hemuppgiften från Matteklubben, åk 7-9
![]()
Delbarhetsprincipen med 11 är inte enkelt att komma fram till, men enkel att använda. Om du vill försöka forska som matematiker, låt bli att googla på vad det är. Försök att svara på följande frågor istället. Skriv i kommentarerna om du har frågor
Första träffen med Matteklubben, åk 7-9
Matteklubben har haft lektioner för grupperna åk 2-4, åk 5-6 och sist ut var högstadieeleverna, åk 7-9.
Denna gång kom en hanterbar mängd elever, 25 stycken. Det är ganska lagom för den åldern, nackdelen med för många elever är att någon som är
Första träffen med Matteklubben, åk 2-4

Minsta eleverna som går i Matteklubben är de i åk 2-4. Du kan också läsa om första lektionen i åk 5-6.
Även om eleverna var små, fyllde de salen så att det nästan blev lite trångt! Totalt var de 40 stycken och denna gång var vi 5 lärare (vi
Första hemuppgiften från Matteklubben, åk 5-6
Här i kommentarerna kan du diskutera hemuppgiften. Skriv om du har frågor eller förslag på lösning/svar.
• Hur många olika armband kan man tillverka av 3 svarta och 2 vita pärlor? På bilden har du ett exempel.
• Hur många svart-vita
Första träffen med Matteklubben, åk 5-6

Matteklubben är Uppsala kommuns satsning på begåvade elever i matematik. Jag har äran att förbereda aktiviteterna som vi håller på med och vara en av lärarna. Här på bloggen tänkte jag lägga ut materialet som vi tar upp på träffarna, samt skriva
Programmering på papper

Fler och fler människor lär sig att programmera, vilket är bra, för fler och fler bra programmerare behövs. Än så länge finns ingen obligatorisk programmering i grundskolan i Sverige, men vem vet, det kanske är på gång?
Jag har undervisat inte
Satsning på begåvade elever i Uppsala

En avhandling startade det hela. Det handlade om situationen för barnen, som har det lätt i skolan. I matematik! Ja, just det, lätt i matematik, inte dem vi brukar betrakta som barn med problem i skolan (och inte heller dem man brukar forska på).
Att räkna utan tal och bokstäver
När någon ställer frågan "Vad är matematik för dig?" svarar jag ibland "Att tänka." Det kan tolkas som ett luddigt svar eller att jag kanske tror att matematik är viktigare än allt annat. Men så är inte riktigt fallet och jag ska försöka visa vad
Perfekta tal och deras binära motsvarigheter
![]()
Nyligen fyllde jag 28 år vilket är en "perfekt" ålder på flera sätt :)
Nämligen är 28 det andra perfekta talet, matematiskt sett. Det vill säga, 28 är lika med summan av alla dess delare, exklusive talet självt:
28 = 1 + 2 + 4 + 7 + 14
Det
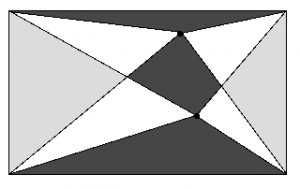
En osynlig yta
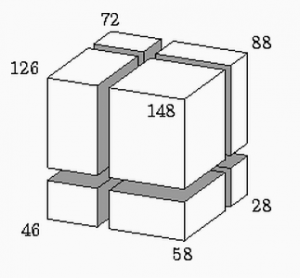
Rekommenderad från: 12 år
[kkratings]
Man gjorde tre snitt och delade upp ett träblock i åtta mindre rätblock. På bilden anges ytarean för de sju synliga bitarna. Hur stor är ytan på den biten som inte syns?
Visa
Hur man klarar 2048-spelet

Om du inte redan har sett 2048-pusslet, som blivit stort online, så kan du testa att spela det på http://gabrielecirulli.github.io/2048 Det går ut på att kombinera ihop tvåpotenser (från början 2:or och 4:or) så att det bildas 2048.
Varning:
Pi-dagen 2014
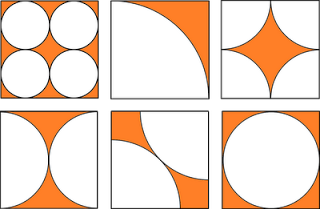
Grattis på Pi-dagen!
Talet pi är förstås relaterat till cirklarnas area och radie, men följande uppgift kan du lösa utan att kunna några formler.
Vilken kvadrat har störst orange area?
(Även om du kan använda dig av formler, prova att
Första matteregattan i Uppsala

Den 1 mars hölls Uppsalas första Matteregatta för högstadiet! Två skolor deltog: Gluntens Montessoriskola samt Uppsala Musikklasser, både respresenterade med ett lag. Stort tack till Katedralskolans mattecirkel som hjälpte till att organisera
Matteskämt

Skämtet är till för en bred grupp läsare som har läst homologisk algebra:
Förklaring
Skämtets skapare: Sebastian Öberg
Sitter du som läsare på några bra/dåliga matteskämt? Skriv gärna i
Decembertävlingen 2013 - resultat och omröstning

Mattebloggens decembertävling är nu avslutad. Tack alla som deltog!
Vinnare
Tävlingens vinnare är en person med kodnamnet $ som fick mest poäng av alla och alltså vunnit ett exemplar av boken Matematisk utflykt. Grattis $!
Alla andra
Korstal 2013

Korstal 2013
[kkratings]
Fyll i precis som ett vanligt korsord (men endast med siffror). Obs! Inga tal börjar med noll.
Lös gärna korstalet tillsammans med familj eller vänner! Ladda ner för
Ett land utan korsningar
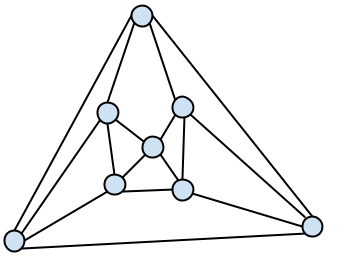
Ett land utan korsningar
[kkratings]
I ett sagoland finns 8 städer. Från varje stad leder 4 vägar och inga vägar korsar varandra. Rita kartan över landet genom att beteckna städerna med punkter och vägarna med
Skuren träkub
![]()
Skuren träkub
[kkratings]
Från varje hörn på en träkub sågade man av en bit så att snittytan på alla ställen blev triangelformad. Hur många hörn och hur många kanter har den kroppen som bildades?
Visa lösningen
Om
Bakteriekoloni
![]()
Bakteriekoloni
[kkratings]
I en bakteriekoloni bestående av tvåhundra bakterier hamnar ett virus. Efter en minut konsumerar viruset en av bakterierna, varpå varje kvarvarande bakterie delar sig i två nya bakterier och viruset
Lastade tunnor
![]()
Lastade tunnor
[kkratings]
Du har 7 fulla, 7 halvfulla samt 7 tomma tunnor. Hur kan du lasta dem på 3 lastbilar, så att varje lastbil får lika tung last?
Visa lösningen
Om lika många tunnor lastas på varje lastbil
Sammansatt tal
![]()
Sammansatt tal
[kkratings]
Hitta det minsta sammansatta talet som inte är delbart med något av heltalen från och med två till och med tio.
Visa lösningen
Om talet inte är delbart med 2, 3, 4, osv. till 10 så betyder
Pepparkakor
![]()
Pepparkakor
[kkratings]
Några barn åt pepparkakor. Var och en åt 7 pepparkakor mindre än alla andra barnen tillsammans. Men varje barn åt ändå upp mer än en pepparkaka.
Hur många pepparkakor åt barnen upp?
Visa
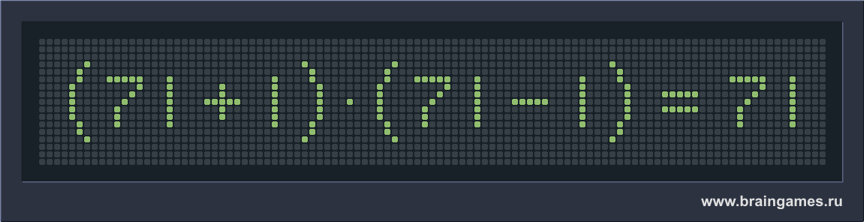
Palindromrebus
![]()
Palindromrebus
[kkratings]
I likheten ersätt stjärnorna med siffror, så att likheten blir korrekt, om båda termerna samt summan måste förbli samma tal om man läser dem från höger till vänster. Talen får inte börja med
Fram och tillbaka igen
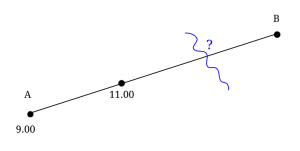
Fram och tillbaka igen
[kkratings]
Från by A till by B leder en enda väg som är 15 km lång. Klockan 9:30 började en hob promenera med hastigheten 4 km/h från A till B. Nästa dag startade han klockan 11:00 från byn B och
HMT-kval 2013
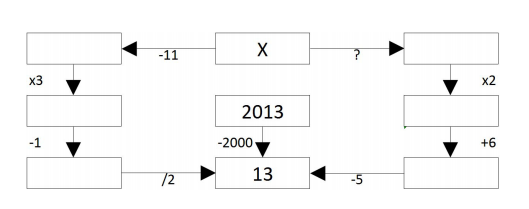
För circa en månad sedan hölls kvalomgången i Högstadiets Matematiktävling. Det är en tävling i problemlösning som riktar sig till årskurs 6-9, men självfallet lyckas eleverna i årskurs 8-9 få bäst resultat. Därför är det mest elever från dessa
Guldkista
![]()
Guldkista
[kkratings]
En kista fylld med guld väger 32 lispund. Samma kista halvfull med guld väger 17 lispund. Hur mycket väger en tom kista?
Visa lösningen
Halva guldet måste utgöra skillnaden mellan vikterna, det
Tjocka och tunna hårband
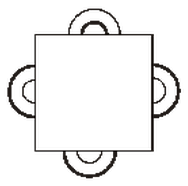
Tjocka och tunna hårband
[kkratings]
På bordet ligger sex hårband som inte nuddar varandra. Ovanpå dem ligger ett papper som delvis täcker dem (se bild). Man vet att tre av hårbanden är tunna, medan tre är tjocka och att
Väldigt lång uträkning
![]()
Väldigt lång uträkning
[kkratings]
Ange resultatet av multiplikationen
$\cdot99\ldots99$$
(2013 stycken nior).
Visa lösningen
$\cdot99\ldots99$$ kan skrivas som $\cdot100\ldots00 - 77 $$ (det stora
Lögnare och sanningssägare
![]()
Lögnare och sanningssägare
[kkratings]
På en ö ute i havet bor lögnare och sanningssägare. Lögnare ljuger alltid, medan sanningssägare talar alltid sanning, och man vet att det finns minst två personer av varje sort på ön.
Excel
![]()
Excel
[kkratings]
Datorprogrammet Excel används för att göra tabeller. I en tabell numreras kolumnerna med hjälp av stora bokstäver. De första 26 kolumnerna är numrerade från A till Z, den 27:e betecknas AA, sedan kommer AB
Utökad produkt
![]()
Utökad produkt
[kkratings]
Det finns tre tal givna. Om alla tal utökas med 1, så kommer deras produkt också utökas med 1. Om alla tal utökas med 2, så kommer deras produkt också utökas med 2.
Hur mycker ökar produkten med
Dividera till fem
![]()
Dividera till fem
[kkratings]
Sätt ut parenteserna i uträkningen så att den blir sann ("/" betyder division)
$/3/4/5/6 = 5$$
Visa lösningen
För att lösningen ska vara korrekt, måste beräkningen vara entydig.
Feta streck
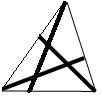
Feta streck
[kkratings]
Triangeln på bilden är uppdelad i fyra trianglar och tre fyrhörningar med de feta strecken.
Fyrhörningarnas omkretser tillsammans är 25 cm. Summan av omkretsarna för de fyra trianglarna är 20 cm.
Ögruppen
![]()
Ögruppen
[kkratings]
I en ögrupp är varje ö kopplad till sju andra via broar. Totalt finns det 84 broar. Hur många öar är det i ögruppen?
Visa lösningen
Vi föreställer oss att en flagga sätts ut vid varje broände
Sju fikabröd
![]()
Sju fikabröd
[kkratings]
Hur kan man dela sju likadana wienerbröd rättvist mellan 12 personer utan att dela upp något bröd i 12 eller fler delar?
Visa lösningen
Det finns flera olika sätt att lösa problemet. Det
Fem punkter på avstånd
![]()
Fem punkter på avstånd
[kkratings]
På ett papper finns fem punkter, som är betecknade A, B, C, D och E. Avståndet AC (dvs avståndet mellan punkten A och punkten C) är 5 cm, avståndet AE är 4 cm, BC = 14 cm, BD = 2 cm, DE =
Problemlösningstävling
![]()
Problemlösningstävling
[kkratings]
Fyra vänner var med i en problemlösningstävling. Katarina löste flest problem av alla, åtta stycken. Eric löste minst problem av alla, fem stycken. Varje problem löstes av exakt tre av
Figur i fyra delar
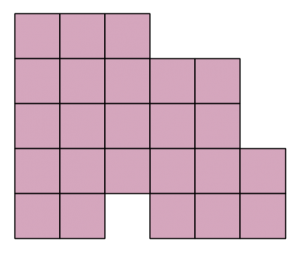
Figur i fyra delar
[kkratings]
Dela upp figuren på bilden i fyra likadana delar.
Visa lösningen
På följande sätt kan man dela upp figuren:
Måla kubens yta
![]()
Måla kubens yta
[kkratings]
För att måla ytan på en kub av storleken 2x2x2 krävs det 2 gram färg. Hur mycket färg krävs det för att måla ytan på en kub av storleken 6x6x6?
Visa lösningen
Ytan på en 6x6x6-kub är
Två delat med två
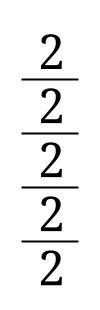
Två delat med två
[kkratings]
Bråkuppställningen på bilden är lite konstig, eftersom det inte går att tyda vad som ska delas med vad i vilken ordning. Du får göra bråkstrecken olika långa för att kunna räkna ut
Schinzels sats
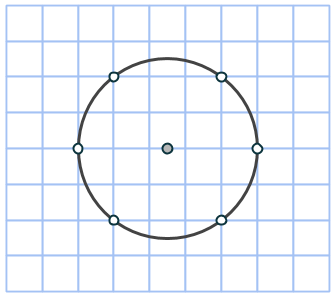
Har du läst om hur man hittar pythagoreiska tripplar i cirklar? I artikelserien träffar vi på många cirklar som har några punkter med heltalskoordinater på periferin.
Men oftast är antalet punkter delbart med 4 (cirkeln är centralsymmetrisk i
Tre påsar med mynt

Rekommenderad från: 13 år
[kkratings]
Du har tre påsar med hundra mynt i varje. I en av påsarna väger alla mynten 9,9g, i en annan väger alla 10g och en tredje väger alla 10,1g, men du vet inte vilka mynt som ligger i vilken påse. Du har
Lösningar till SMT-kvalet 2013
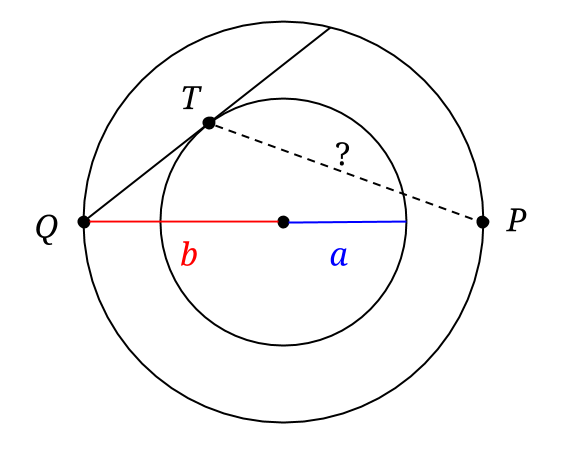
Nyligen hölls SM i matte för gymnasister, som kallas Skolornas Matematiktävling. Tävlingen bestod av 6 uppgifter som eleverna fick lösa under 5 timmar.
De officiella lösningarna har inte kommit upp än, så jag tänkte föreslå egna. Samt kommentera på
Pythagoreiska tripplar i form av areor, del 4
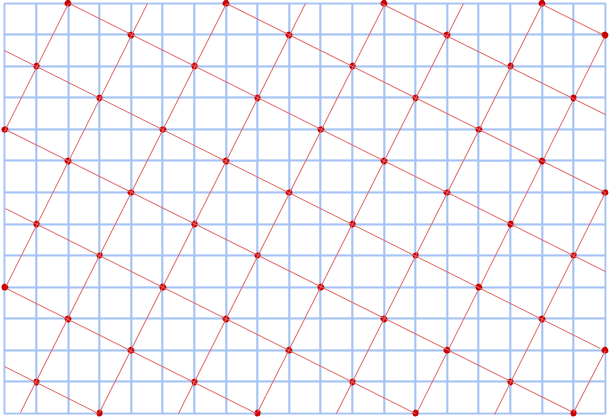
I föregående del avslöjade vi processen med vilken vi kan förstora koordinatsystem på så sätt att de förstorade ciklarna innehåller icke-primitiva pythagoreiska tripplar.
Om ett heltal kan representeras som en summa av två kvadrater, så kan vi
Pythagoreiska tripplar i form av areor, del 3
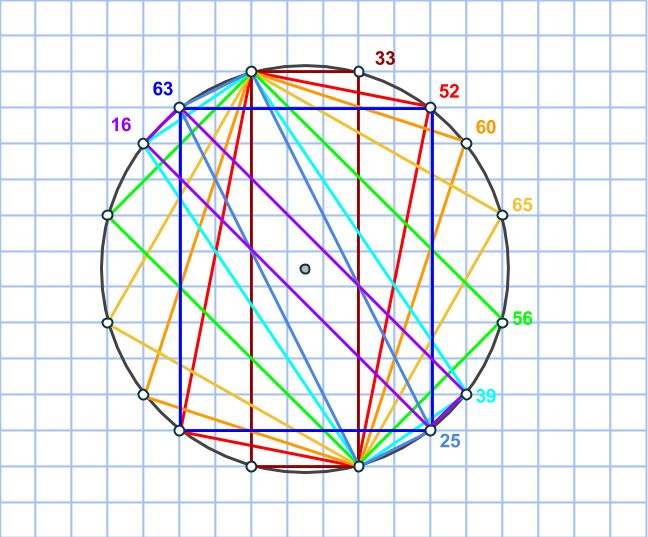
I del 2 såg vi att en primitiv pythagoreisk tripplel alltid kan representeras i form av rektangelareor (inuti rutnätscirklar).
Dyker det upp exakt 3 olika rekatngelareor inuti en sådan cirkel?
Nej, det kan dyka upp fler än så, vilket beror på
Pythagoreiska tripplar i form av areor, del 2
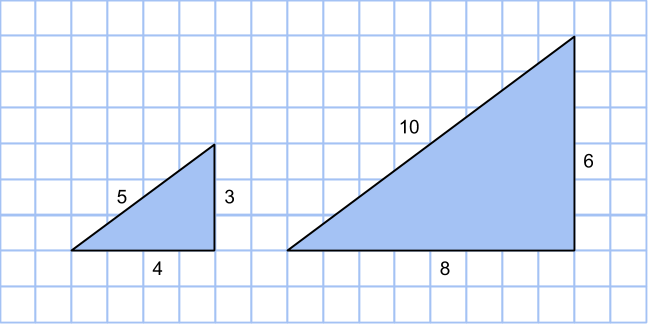
I del 1 såg vi hur vissa pythagoreiska tripplar kunde representeras i form av areor på rektanglar inuti cirklar på rutnät. I den här delen undersöker vi huruvida detta är möjligt för alla primitiva tripplar.
Primitiva pythagoreiska tripplar
Pythagoreiska tripplar i form av areor, del 1

[kkratings]
Föreställ dig ett rutnät av punkter. Det går att hitta massvis med cirklar som går igenom några av punkterna. En av de minsta sådana cirklarna har hela 8 punkter på sin rand:
Det går även att hitta några rektanglar inuti sådana
Tärningsspel för små barn
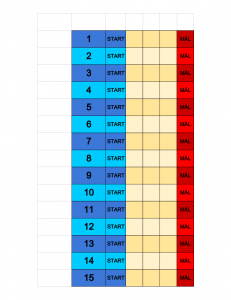
Ett enkel spel med tärningar
Rekommenderas för
Förskolan, lågstadiet, mellanstadiet
Materiel
Ett spelplan (skriv ut nedan), två vanliga sexsidiga tärningar (helst av olika färger), minst 4 pjäser (från "Fia med knuff" till exempel)
Tid
Godis laget runt
Rekommenderad från: 12 år
[kkratings]
Någon skickade ut sin stora godispåse runt bordet: första personen tog 1 godis, nästa tog 2, nästa tog 3 och så vidare, det vill säga nästa person tog alltid en godis mer än den föregående. Under
Phi-växter, pi-växter och e-växter, del 2
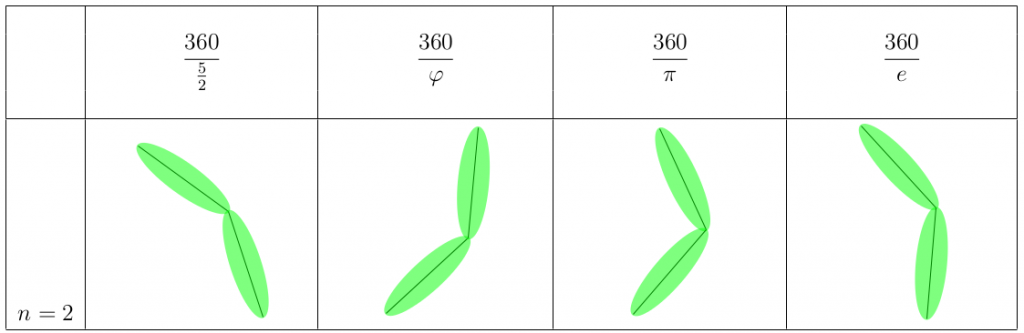
I del 1 kom vi fram till att en växt inte bör växa med en rationell vinkel. Det vill säga, om vinkeln bladen emellan är 360/(p/q), så kommer växter sabba solljuset för sig själv efter p blad.
Om p=5 och q=2 så växer bladen ut med 360/(5/2)= 144
Phi-växter, pi-växter och e-växter, del 1

Hur kommer det sig att det finns spiraler på kottar, kronärtskockor och ananaser? Om du inte har sett förklaringen, rekommenderar jag Vi Harts videoserie "Spirals, Fibonacci, and Being a Plant": del 1, del 2 och del 3.
(Eller kolla upp en sida på
Sudoku med femrutiga block

Rekommenderad från: 11 år
[kkratings]
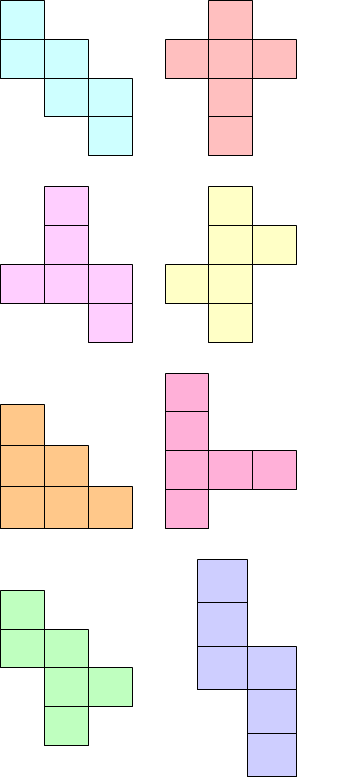
Måla rutorna i figuren nedan i 5 färger på så sätt att rutorna i varje rad, varje kolonn, samt varje markerad 5-rutig figur blir olikafärgade.
Visa lösningen
Man kan börja måla en hel
Bollvolymer i n dimensioner

Det är lätt att med experiment uppskatta volymer av olika tredimensionella kroppar: Exempelvis kan ett akvarium i from av en rätblock fyllas med vatten och sedan kan man mäta hur mycket vatten som gick åt. Samma kan göras med (ungefär) sfäriska
Oändlig choklad

En triangel kan ju delas i delar, byggas om och bli totalt en ruta mindre, se inlägget Fibonaccitalen och gyllene snittet.
Men samma princip kan utnyttjas för att få en ruta mer av en rektangel, vilket ger oss ett utmärkt sätt att äta choklad
Påskens Skönhetstävling

Rekommenderad från: 13 år
[kkratings]
I Påskens Skönhetstävling deltog Hönan, Tuppen och Kyckligen. Varje domare röstade på en av deltagarna. Påskharen räknade att det var 59 domare, där de gav 15 röser till Hönan och Tuppen sammanlagt,
Hur man multiplicerar matriser
![]()
Ju mer matteförklaringar är intuitiva, desto mer gillar jag dem. Matematik är svårare att förklara bättre på video än IRL på en tavla, men det finns undantag och det är då videoformen utnyttjas som mest.
Jag är nöjd över att ha hittat följande
Två bokhögar

Rekommenderad från: 12 år
[kkratings]
På ett bord ligger en boksamling av barnböcker i 10 delar, uppdelade i två högar. Du får ta tag i en stapel (några av de översta böckerna i en hög, som minst en, som mest hela högen) och placera
Hur långt är det till horisonten?

Om du någonsin undrat hur långt det är till horisonten, så förklaras det i den tyska låten nedan.
Mer matematisk konst åt
Pizzasats nummer 2
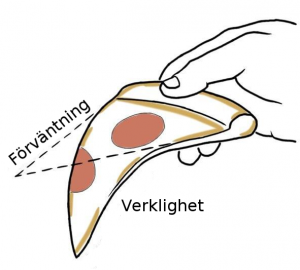
Matematik används inte bara när man ska skära upp pizza, utan också när man ska äta den. Möjligen har ni löst problemet nedan utan att ens tänka på matte.
När en pizzabit tas ut ur kartongen ser det ofta ut så här:
Mot detta finns följande
Pizzasats nummer 1

Geometri är inte bara någonting skäggiga greker höll på med, utan den kan vara användbar även för den gemene svensken - till exempel när man ska dela en rund pizza!
Om man får en pizza hemkörd och ska dela den på två personer, så brukar man skära
Datum med träblock

Rekommenderad från: 11 år
[kkratings]
Min bror ställer in datumet varje dag med hjälp av fem träblock.
Tre av dem är av avlånga och används för månaderna.
De andra två är kuber. Vilka siffror kan stå på kubernas sidor
Gardners drake

Du har säkert bilder eller monument där någon tycks följa dig med ögonen när du passerar. Men har du någonsin träffat en konstgjord varelse som följer dig med hela huvudet?
(Vänta ett tag innan videon laddas, det är värt
Korstal 2012

Korstal 2012
[kkratings]
Fyll i precis som ett vanligt korsord (fast nu endast med siffror). Obs! Inga tal börjar med noll.
Ladda ner för utskrift.
Vågrätt:
1. Tvåpotens.
6. Siffersumman för lodrätt 13,
Att dela rättvist
![]()
Att dela rättvist
[kkratings]
En vandrare gick förbi två kompisar som skulle äta pannkakor. Ena kompisen hade 3 pannkakor, den andra hade 4 pannkakor. Alla pannkakorna delades jämnt mellan de tre personerna. Vandraren
Datum med två siffror
![]()
Datum med två siffror
[kkratings]
Dagens datum är lite ovanligt: 121222. Vilket blir nästa datum som skrivs med högst två olika siffror (om datumet betecknas med 6 styken siffror)?
Visa lösningen
Nästa datum med
Att rita tre kvadrater
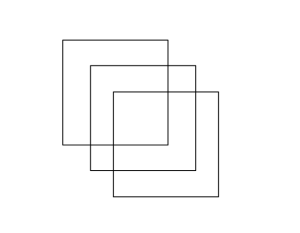
Att rita tre kvadrater
[kkratings]
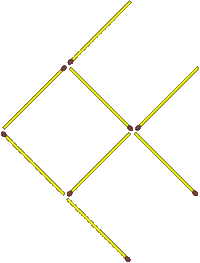
Går att rita följande figur utan att lyfta pennan från pappret? Det är inte tillåtet att dra samma sträcka flera gånger.
Visa lösningen
Ja, det går! Följ bara pilarna med
Val i Bananrepubliken

Val i Bananrepubliken
[kkratings]
I riksdagsvalet i Bananrepubliken deltog alla landets medborgare. Alla som röstade på Clementinpartiet tycker om clementiner. Bland dem som röstade på de andra partierna tycker 90% inte
Kryssa grannrutor

Kryssa grannrutor
[kkratings]
Chiyen satte ett kryss i en ruta på en rektangel. Esteban får sätta kryss i de andra rutorna, men bara om de uppfyller följande regel: man får bara kryssa i rutor som har ett udda antal
Bilar i Mexico
Bilar i Mexico
[kkratings]
Mexico bestämde sig för att införa en ny lag, som innebär att varje bil i landet måste stå obrukad minst en dag i veckan (ägaren måste meddela polisen vad registreringsnumret är och vilken
Rubiks kub utan hörn
Rubiks kub utan hörn
[kkratings]
Man tog bort alla hörn från en Rubiks kub. Skulle en sådan konstruktion kunna sättas ihop av rätblock med 1x3-kuber?
Visa lösningen
Det går inte, eftersom antalet småkuber som
Kulor i olika färger
![]()
Kulor i olika färger
[kkratings]
Tre personer A, B och C räknade antalet julgranskulor av olika färger på granen. Var och en kunde skilja på två av färgerna, men de andra två kunde hen förväxla: En av dem förväxlade
Tätt med punkter på linjen
![]()
Tätt med punkter på linjen
[kkratings]
På en linje fanns några punkter. Man gjorde det mer tätt mellan punkterna: det sattes ut en ny punkt i varje mellanrum mellan två gamla punkter. Man gjorde det tätare mellan punkterna
Tretton punkter

Tretton punkter
[kkratings]
Dra fem streck utan att lyfta pennan från pappret så att strecken går igenom alla 13 punkterna:
Visa lösningen
Tricket är att gå utanför figuren som punkterna bildar:
Följder med regel
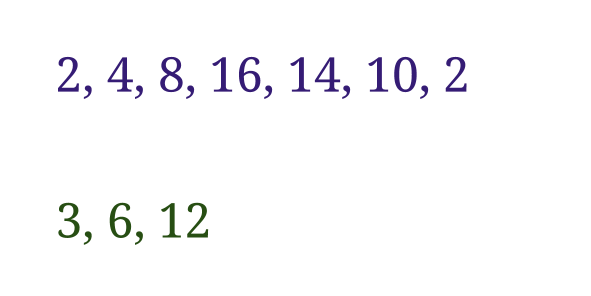
Följder med regel
[kkratings]
Du får se två följder med tal:
Det finns en regel som utifrån varje tal bestämmer nästa tal.
(a) Vad är det för regel?
(b) Bestäm alla positiva heltal som enligt regeln blir sig
Trapets till en triangel
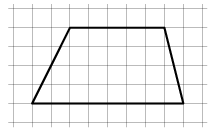
Trapets till en triangel
[kkratings]
Dela upp figuren nedan i två delar som kan sättas ihop till en triangel.
Visa lösningen
Dela upp trapetset genom att dra en linje från ena hörnet till mitten av en motsatt
Ett tal med åtta siffror

Ett tal med åtta siffror
[kkratings]
Kan man hitta på ett tal som består av 8 olika siffror, så att talet är delbart med alla siffror som ingår i det?
Visa lösningen
Låt oss anta att ett sådant tal finns.
Då
Bläckfiskarnas armar

Bläckfiskarnas armar
[kkratings]
I havet bor bläckfiskar med 6, 7 eller 8 armar. De som har 7 armar ljuger alltid, medan de som har 6 eller 8 armar talar alltid anning.
Fyra bläckfiskar möttes en gång. Den blåa sade:
Åtta liter

Åtta liter
[kkratings]
Du befinner dig vid en å i skogen och du har två hinkar med dig: den ena rymmer 15 liter, den andra rymmer 16 liter. Kan du mäta upp exakt 8 liter vatten? Hinkarna saknar några som helst
Julklappen i lådan
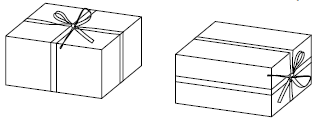
Julklappen i lådan
[kkratings]
En julklapp ligger i en låda med kvadratisk bas. Lådans höjd är hälften så långt som basens sida. Man kan linda ett 156 cm långt snöre runt lådan och göra en rosett som på bilden till vänster.
Figur i tre delar
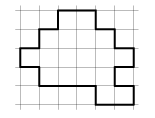
Figur i tre delar
[kkratings]
Dela upp figuren nedan i tre likadana delar.
Visa lösningen
En kung som gillade att bygga

En kung som gillade att bygga
[kkratings]
I Sagolandet fanns en kung som tyckte mycket om att bygga. En gång bestämde han sig för att bygga 6 torn och anlägga vägar mellan varje par av torn, men på så sätt
att det bara
Rätt antal
![]()
Rätt antal
[kkratings]
Fabian sade till Artem att räkna antalet grafer han hade ritat i skrivblocket. "Ta antalet grafer, addera 7, sedan dividera resultatet med 8, sedan multiplicera med 6 och sedan subtrahera 9. Då kommer
Egentillverkad tärning

Egentillverkad tärning
[kkratings]
Lars tillverkade en tärning, där han satte ut 1, 2, 3, 4, 5 respektive 6 prickar på sidorna. Sedan kastade han tärningen två gånger. Första gången blev summan av alla prickar på de fyra
Uppdelad rektangel
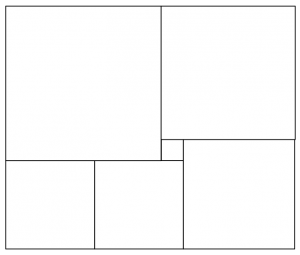
Uppdelad rektangel
[kkratings]
En rektangel är uppdelad i 6 kvadrater (se bilden nedan). Hur stor är den största kvadraten om den minsta har sidlängden 1cm?
Obs! Figuren är inte nödvändigvis perfekt, därför räknas det inte
Fyra lika kompisar

Fyra lika kompisar
[kkratings]
Fyra kompisar är lika varandra på många sätt: vilket par av dem man än tittar på, så har det paret samma tilltalsnamn eller samma efternamn eller samma födelsedatum. Däremot har inga tre av
Två magiska tal
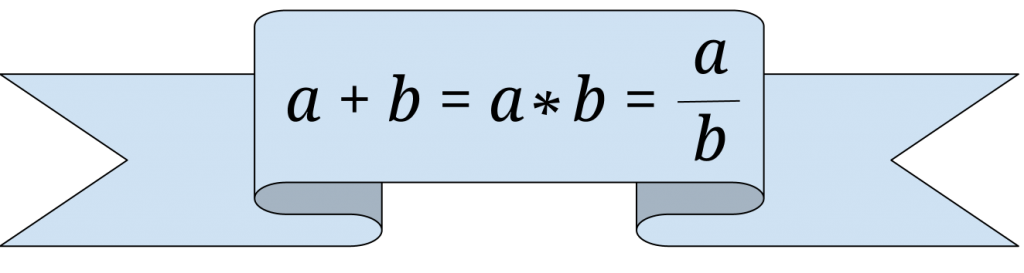
Två magiska tal
[kkratings]
Finns det två tal, sådana att deras summa, produkt, samt kvot sammanfaller?
Visa lösningen
Antag att sådana två magiska tal a och b existerar.
Om a*b = a/b, så måste a*b*b = a.
Trassel (tangles)
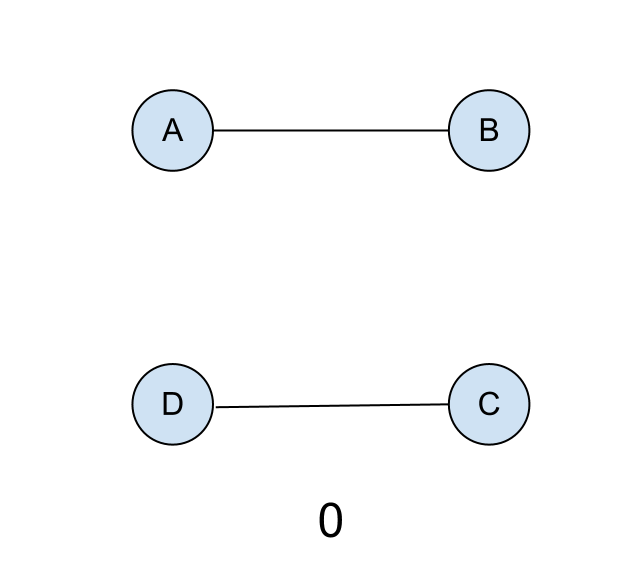
Aktiviteten trassel
Rekommenderas för: gymnasieet, universitetet (eller i förenklad form för högstadiet)
Materiel: två stora rep eller sladdar (gärna av olika färger), en ogenomskinlig plastpåse
Tid: 45 minuter
Antalet deltagare: 4 + publik
Klurig fyrhörning
![]()
Rekommenderad från: 17 år
[kkratings]
En konvex fyrhörning ABCD har kända sidlängder: AB = 5, BC = 10, CD = 14, DA = 11. Fyrhörningens diagonaler skär varandra med en viss vinkel. Hur stor är den vinkeln?
Visa
Bas 10

En alien med 4 fingrar och en människa möter varandra:
Vad är en bas?
De flesta förstår räkning med olika baser utan att behöva lära sig någon formell definition. Vi räknar i bas 10 och det finns ental, tiotal, hundratal och så vidare. Vi
Kvaternioner

Enligt en broinskription (se bilden nedan) upptäcktes kvaternionerna för exakt 169 år sedan, då William Hamilton tog en promenad i Dublin med sin fru. Hamilton kände till de komplexa talen (till exempel talet $$i$$ som uppfyller likheten $$i\cdot i
Världens mest matematiska flagga

Fråga: Vilket land har längsta matematiska texten i sin konstitution?
Svar: Nepal, som har inkluderat den geometriska konstruktionen av sin flagga i konstitutionen. Landet är dessutom den enda i världen vars flagga inte är
Aladdin och grottan

Rekommenderad från: 12 år
[kkratings]
Aladdin vill komma in i grottan, men dörren än stängd. Innanför grottan finns en tunna med fyra hål (hålen är likadana och är placerade som hörnen på en kvadrat). I varje hål finns en karaff med
Calkin Wilf-träd, del 3
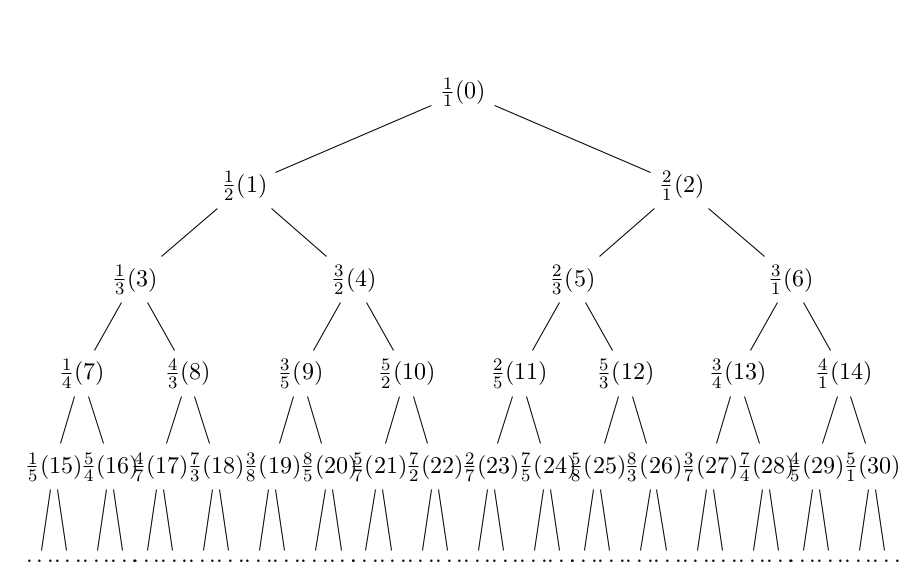
Matematiken är full av vackra oväntade kopplingar, som mellan ett träd av bråk och ett gammalt taluppdelningsproblem.
Hittills har vi konstaterat att antalet sätt att dela upp ett tal i en summa av tvåpotenser, där ingen potens förekommer fler
Calkin Wilf-träd, del 2

År 1858 ställde tyska matematiker Stern och Moritz en fråga: På hur många sätt kan man skriva talet n som en summa av tvåpotenser, där var tvåpotens får förekomma högst två gånger? (Ordningen på termerna i summan spelar inte någon roll).
Till
Calkin Wilf-träd, del 1
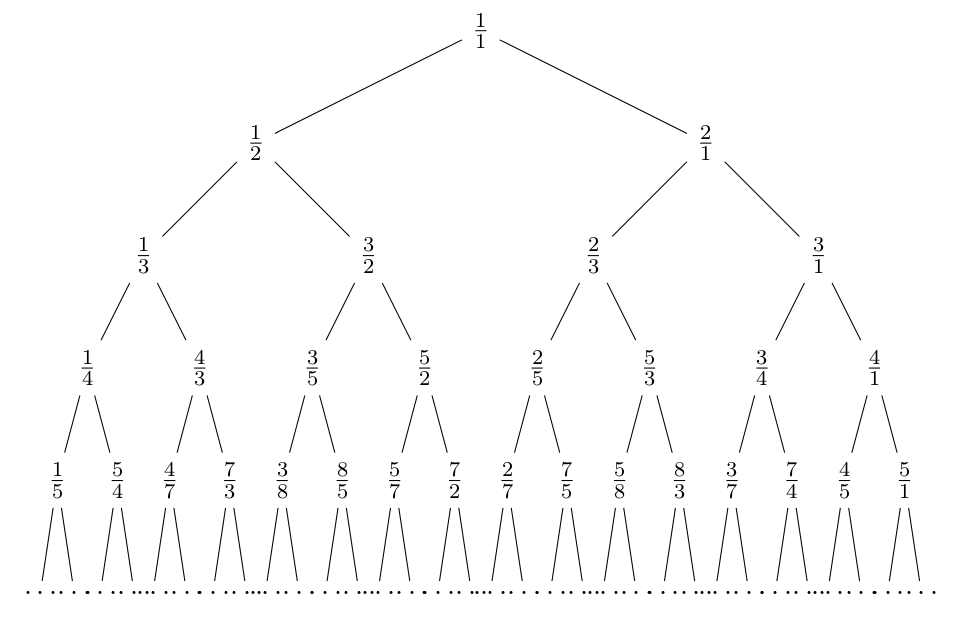
Det är sällan som nya matematiska upptäckter handlar om någonting enkelt. All matematik som lärs ut i grundskolan upptäcktes för länge sedan av gamla greker, araber, kineser och indier. Gymnasiematematiken baserar sig på upptäckter som är minst 300
Öva på geometri inför SMT-kval

Kvalomgången i Skolornas matematiktävling sker imorgon. Om du vill fräscha upp era geometrikunskaper inför tävlingen
här står det korfattat vad du behöver plugga på. Notera att minst ett av problemen på tävlingen är ett klassiskt
Öva på delbarhet och ekvationer inför SMT-kval

Skolornas matematiktävling närmar sig med stormsteg, nu är det bara en vecka kvar! Jag har skrivit tips inför tävlingen förut, men om du träna på verkliga problem, rekommenderar jag att kolla på vår cirkellektion, som handlade just om delbarhet,
Tvåpotenser

Talen på formen $^n$$ dyker upp på många ställen. Finns det en cell som fördubblar sig varje minut, så finns det efter en minut 2 celler. Efter ytterligare en minut finns det 4 celler, sedan 8, sedan 16, 32, 64, 128...
Väldigt ofta dyker även
Vad är ett fullständigt bevis?
![]()
När man löser ett riktigt matematiskt problem räcker det inte att presentera svaret. Du måste presentera lösningen också, det vill säga hur du kom fram till svaret. Ibland har inte problemet något svar, utan du skall bevisa att något påstående är
Ett osannolikt möte

Tack till Lisa Lokteva för att hon tipsade mig om nedanstående problem:
Rekommenderad från: 15 år
[kkratings]
Två personer anländer oberoende av varandra till en bestämd plats mellan 9.30 och 10.00. De stannar på platsen i exakt tre
Måla egna fraktaler

Har du alltid velat att rita egna fraktaler, men inte vetat hur man gör?
Grundprincipen för en fraktal är ett mönster som upprepar sig inuti figuren om och om igen. De mest kända exempel är:
Sierpinskis triangel
En liksidig triangel delas
Roliga spel med tråkiga ekvationer

De flesta människor tycker inte om algebra i skolan. Utan någon intuition för vad som händer tvingas de att lösa ekvationer i skolan. Och när ekvationen väl är löst finns det ingen känsla av tillfredsställning, snarare kvarstår förvirringen och
Bäst resultat vinner!
Den senaste träffen på Katedralskolan genomförde vi en liten tävling bland deltagarna.
Varje deltagare fick 5 stycken problem att lösa på kort tid. Dock behövde inte problemen lösas fullständigt, utan det viktiga var att uppnå ett resultat. Men
Problemlösning lådprincipen

Den här vårterminen har jag äran att tillsammans med en annan lärare leda problemlösningskursen på Katedralskolan i Uppsala! Vi håller 2 timmarslektioner för intresserade elever på skolan, samt för nior som ska börja läsa där.
Tanken med träffarna
Polisbilen

Rekommenderad från: 15 år
[kkratings]
En polisstation befinner sig på en väg som sträcker sig oändligt långt åt båda håll. Någon stal den gamla polisbilen, som har maxhastigheten lika med 90% av den nya polisbilens
En lektion för små barn i topologi

Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.
Här kan du se vad vi tidigare har gått igenom.
Former
Topologi handlar om olika slags
Problemlösning heltalsekvationer
![]()
Den här vårterminen har jag äran att tillsammans med en annan lärare leda problemlösningskursen på Katedralskolan i Uppsala! Vi håller 2 timmarslektioner för intresserade elever på skolan, samt för nior som ska börja läsa där.
Tanken med träffarna
Fiskens bana
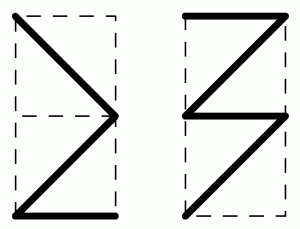
Rekommenderad från: 12 år
[kkratings]
Någon antecknade fiskens bana i ett akvarium sett framifrån (första bilden) och någon annan ritade banan sett högerifrån (andra bilden). Hur såg fiskens bana ut om man kollade
Problemlösning intro
![]()
Den här vårterminen har jag äran att tillsammans med en annan lärare leda problemlösningskursen på Katedralskolan i Uppsala! Vi håller 2 timmarslektioner för intresserade elever på skolan, samt för nior som ska börja läsa där.
Tanken med träffarna
En lektion för små barn i mönster och spatial förmåga

Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.
Här kan du se vad vi tidigare har gått igenom.
Mönster
Väldigt mycket i
Pilen
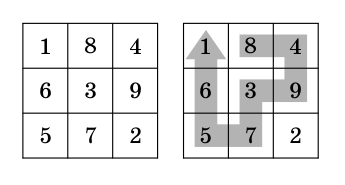
Rekommenderad från: 10 år
[kkratings]
Siffrorna 1 till 9 fyller kvadraten som det syns på den vänstra bilden. Man får gå på kvadratens rutor, men aldrig tillbaka till en ruta man varit på förut, och man måste alltid gå till en
En lektion för små barn i grafteori

Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.
Här kan du se vad vi tidigare har gått igenom.
Grafer
Jag försökte att
Lejonet på arenan

Grattis på pidagen!
Rekommenderad från: 17 år
Förkunskaper: radianer, transformationer.
[kkratings]
Ett lejon springer runt på en rund cirkusarena, som har radien 10 m. Lejonets bana består av raka streck och i slutändan springer
En lektion för små barn om kvadrater (och andra fyrhörningar)
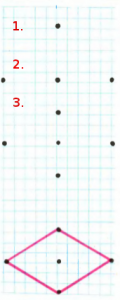
Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.
Här kan du se vad vi tidigare har gått igenom.
Fyrhörningar
Vad är en
So you think you can derive?
![]()
Jag hjälper en person med att förbereda sig inför en tenta i endimensionell analys och vi träffar på följande tentauppgift:
$$ \text{Derivera} \ \ x^{\sin x}$$
Tror du att du kan derivera rätt på första försöket? Prova och se om du
Annorlunda tideräkning
Rekommenderad från: 12 år
[kkratings]
Invånarna på Matteön delar in dygnet i timmar, timmar i några minuter och minuter i några sekunder. Men deras dygn består av 77 minuter och deras timme innehåller 91 sekunder. Hur många sekunder
En lektion för små barn i kombinatorik

Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.
Här kan du se vad vi tidigare har gått igenom.
Kombinatorik
Kombinatorik är
Spänd tråd

[kkratings]
I en vägg sitter tjugo spikar (se bilden). Avståndet mellan två spikar som sitter precis bredvid varandra är 1 cm.
Din uppgift är att spänna en 19 cm lång tråd mellan spik 1 och spik 2, så att den går igenom alla
En lektion för små barn om trianglar

Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.
Notera att barnen redan har haft två lektioner om vinklar och olika
Språkkunskaper

[kkratings]
På en gymnasieskola tillfrågade man alla elever om vilka språk de kunde. Det visade sig att fler än 90% kunde både engelska och tyska, samt att fler än 90% kunde både engelska och franska.
Visa att bland de elever som
Introducera x tidigt i skolan?
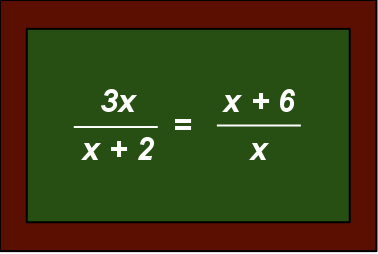
Nyligen pratade jag med en kollega om ekvationer. Att så pass måna barn och ungdomar i Sverige har svårt att förstå hur ekvationer funkar.
En möjlig förklaring till detta är att det blir för stort hopp i abstrakt tänkande när ekvationer först
En lektion för små barn om vinklar på klockan och delbarhet
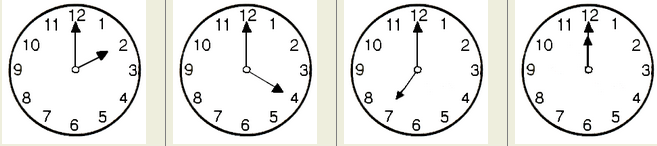
Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.
Notera att barnen redan har haft en introduktion till vinklar och olika
Centauren
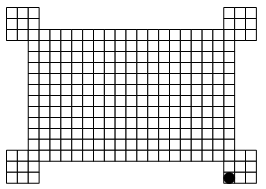
[kkratings]
Två spelare spelar på ett oregelbundet rutigt bräde. De turas om att flytta pjäsen Centauren, som kan flyttas antingen en ruta åt vänster, en ruta uppåt eller en ruta uppåt-höger på ett drag.
Spelaren som inte kan flytta
En lektion för små barn om vinklar
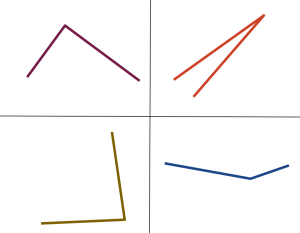
En ny termin är igång och för mig innebär det söndagsträffar med mina matematiksugna 5-, 6-, 7- och 10-åringar! Förra terminen skrev jag om våra 6 träffar, men vi har egentligen haft 11 stycken och i vår ska vi ha ungefär lika många!
Gamla
HMT-final 2012 och föredraget om spel

Lördagen den 21 januari var en spännande dag för ca 45 högstadieelever. De tävlade nämligen i junior-sm i matte, det vill säga finalen i Högstadiets Matematiktävling!
Vinnaren blev precis som förra året Lisa Lokteva från Borås, denna gång på en
Roliga mattegåtor?
![]()
Nu har alla adventsgåtorna fått lösningar, kolla upp dem under respektive inlägg.
Samtigit har jag lagt in en ny mätare på varje mattegåta (från december 2011), där ni kan bedöma hur rolig gåtan egentligen var. Jag skulle vara väldigt tacksam
Mattekorsord 2011

Jag behåller traditionen och presenterar ett sifferkorsord även i år. Denna är lite svårare än förra året, men också lite mindre. Utmana dina nära och kära eller lös korstalet tillsammans.
God Jul önskar mattebloggen!
Mattekorsord
Hungrig student

Hungrig student
[kkratings]
Pelle har en stekpanna som det får plats två hamburgare i samtidigt. Han vill steka varje hamburgare på varje sida i 2 minuter. Pelle är hungrig och vill steka tre hamburgare så fort som möjligt.
Triangellandet

Triangellandet
[kkratings]
Triangellandet har formen av en liksidig triangel. En inre gräns delar landet i två stater, som har lika stor area. Beskriv hur gränsen ser ut (formen och positionen) om den har den minsta möjliga
Sifferrebus
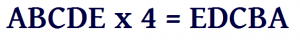
Sifferrebus
Vilka siffror passar istället för bokstäverna? (Varje bokstav är en unik siffra.)
Visa lösningen
Eftersom talet fortfarande har fem siffror efter multiplikationen, får inte A var för stort. A=1 eller A=2 fungerar. Men å andra
Polyedrar och polygoner
Polyedrar och polygoner
[kkratings]
Visa att varje polyeder har minst två sidor som är polygoner med lika många hörn.
Visa lösningen
Antag att det finns en polyeder där alla sidor har olika antal hörn. Ta då den
Kronans massa

Kronans massa
[kkratings]
En krona som väger 60 minor (en mina är en antik viktenhet) är gjord på en legering av guld, koppar, tenn och järn. Guld och koppar utgör 2/3, guld och tenn - 3/4, guld och järn - 3/5 av hela kronans
Tetris
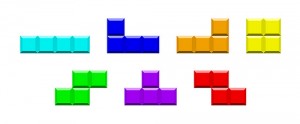
Tetris
[kkratings]
I tetris används sju brickor:
Går det att använda alla brickorna och bygga:
a) en rektangel med formen 4x7
b) en "triangel"?
Visa lösningen
Varken figur a) eller figur b) går att bygga.
Schackpjäs

Schackpjäs
[kkratings]
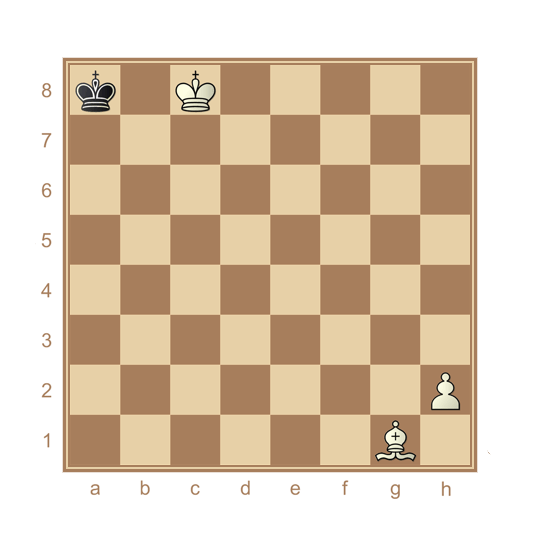
Vilken pjäs står på rutan h4 i den här schackpositionen?
Visa lösningen
Det kan inte precis ha varit svarts tur, eftersom svart kung är under schack. Alltså har vit precis gjort ett drag. Vit
Änglarna på granen

Änglarna på granen
[kkratings]
Fyra änglar sitter på en julgran bland all pynt. Två av dem hade blå glorior och två hade gula. Änglarna vet inte vem som har vilket sorts gloria, men alla vet vem som kan se vem (se
Kamelen och bananerna

Kamelen och bananerna
En kamel odlar bananer. Det här året fick han bästa skörden någonsin: 3000 bananer! Men tyvärr ligger den närmaste platsen där han kan sälja bananerna 1000 km bort. Kamelen kan bara bära 1000 bananer i taget och på vägen
Triell
Triell
[kkratings]
A, B och C deltar i en triangelduell med pistoler. Alla vet att A träffar med sannolikheten 0,3. Sannolikheten att C träffar är 0,5, medan B missar aldrig. Deltagarna skjuter en i taget mot en vald person
Hundra
![]()
Hundra
[kkratings]
Du kan sätta ut parenteser, plus-, minus-, gånger- och delat med-tecken i vänsterledet. Går det att åstadkomma likhet på så sätt?
9999999 = 100
Visa lösningen
Ja, till exempel så här: (99 - 9)/9
Ålder

Ålder
[kkratings]
En man fick frågan: "Hur gammal är du?" Han svarade: "Jag är ganska gammal. Jag är sexhundra gånger äldre är några av mina släktingar."
Kan mannen tala sanning?
Visa lösningen
Ja, det kan vara
Ett väldigt delbart tal

Ett väldigt delbart tal
[kkratings]
Talet 310 är delbart med både 31 och 10. Hitta på ett så stort tal som möjligt, som är delbart med alla tvåsiffriga tal som grannsiffrorna i talet utgör. Det är inte tillåtet att ha nollor inuti
En heltalskub
En heltalskub
[kkratings]
För en viss kub räknade man ut följande tre tal: summan av alla sidlängder, ytan, samt volymen. Alla talen, uttryckta i centimeter/kvadratcentimeter/kubikcentimeter, är tresiffriga heltal. Hur lång
Test utan text

Ett till logikproblem till alla!
Test utan text
[kkratings]
Camelia pluggade hårt inför ett test. Hon kollade på frågorna och svaren på förra årets test, men upptäckte att en av frågorna blev dåligt utskriven. Svaren syntes
Komma över till andra sidan

Kanske har du hört problemet om bonden och hans ägodelar. Det här är en annan variant på problemet!
Komma över till andra sidan
Det finns en båt med plats för tre och en av platserna är reserverad åt bonden. Bonden måste komma över till andra
Vattenmelon

Vattenmelon
[kkratings]
En nyköpt vattenmelon vägde 10 kilogram och bestod till 99% av av vatten. Efter ett tag torkade den ut och nu består den till 98% av vatten. Hur mycket väger vattenmelonen nu?
Visa
Ädelstenar

Ädelstenar
[kkratings]
Dario fick en stor säck i julklapp av en väldigt rik person. I säcken ligger sjukt många ädelstenar, gröna och gula, men han kan inte avgöra på formen vilken färg de har. Dario tar ut 100 ädelstenar på
Trigonometrisk rebus

Dagens gåta är en sifferrebus. Notera att trigonometriska "formeln" inte stämmer.
Trigonometrisk rebus
[kkratings]
Kevin ställde upp en addition, men sedan döljde uträkningen genom att byta ut siffror mot bokstäver
Bräde

Bräde
[kkratings]
Ett bräde är indelad i 4x4 rutor. Du får såga längs med de små rutdiagonalerna (det går bra att såga i båda diagonalerna på en vissa ruta). Hur många små diagonaler kan du som mest såga utan att brädet faller
Rektangel

Rektangel
[kkratings]
Du har tillgång till 12 sträckor som är 2cm långa, 12 sträckor som är 3cm och 11 sträckor med längden 5cm. Går det att bygga en rektangel av alla sträckorna med sidlängderna lika med ett helt antal
Tre brev

Tre brev
Du har fått tre brev och måste omedelbart äta upp ett av dem. I varje brev finns en lapp med två meningar. I ett av breven är båda meningarna goda råd, i ett annat är båda dåliga råd och det tredje innehåller ett gott och ett dåligt
Femkronors-spel

Femkronors-spel
Erik och Sixten spelar ett spel mot varandra. Reglerna är enkla: de turas om att lägga femkronors-mynt på ett runt bord (som från början är tomt). Mynten som redan är lagda ligger kvar till slutet av spelet. Den pojken, som inte
Lösningar till Sonja Kovalevsky-dagarnas problem 2011

I helgen har Sonja Kovalevsky-dagarna varit i Stockholm för andra året i rad. Och fjärde året i rad har jag hjälpt till med problemlösningsdelen :)
Här är tävlingsproblemen och lösningar för de
Tips inför SMT-final
![]()
Som vanligt lite sent kommer det några tips inför morgondagens tävling! De allmäna tävlingstipsen gäller förstås fortfarande.
Saker som är bra att kunna inför finaltävlingen utöver det man ska kunna inför kvaltävlingen:
- Triangelolikheten
-
Logiskt tänkande med små barn: träff 5 och 6
Jag fortsätter mina lektioner med små barn i Stockholm. Läs om de föregående träffarna:
1 & 2
3 & 4
eller fortsätt läsa det här inlägget. Notera att ordningen inte är kronologisk och att inte alla aktiviteter förekommer på alla
Logiskt tänkande med små barn: träff 3 och 4

Jag fortsätter mina lektioner med små barn i Stockholm. Läs om de första två träffarna eller fortsätt läsa det här inlägget. Notera att ordningen inte är kronologisk och att inte alla aktiviteter förekommer på alla lektioner.
Geometri för
Var kommer talet e ifrån?
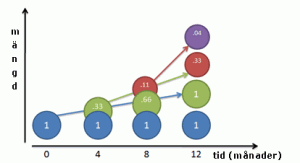
Jag hade själv länge ingen intuitiv förståelse för $$e$$. Jag visste att funktionen $$e^x$$ hade sig själv som derivata och att funktionen hade en snygg Taylorutveckling. Men inte så mycket vad det hade med naturen att göra.
Tills jag träffade på
Tips inför SMT-kval
![]()
Nu är det bara några timmar kvar till SMT-kval och jag tänkte dela av mig med mina tävlingstips.
Allmänna tävlingstips:
- Ha skoj! Det här är bara en tävling.
- Slösa inte bort tiden, fem timmar kan gå väldigt fort! Gör ett gott försök att
Logiskt tänkande med små barn: träff 1 och 2
Denna höst har jag börjat jobba på ett helt nytt sätt. Jag undervisar fem- och sexåringar i matte i ryska klubben "Kolobok" i Stockholm! En gång i veckan träffar jag fyra grupper med barn mellan (en med femåringar, två med sexåringar och en med
Sista dagen för att anmäla dig till matematik-SM!
![]()
Nu är det snart igång igen! Sverige väljer sina skarpaste hjärnor bland gymnsieeleverna för att i sommar skicka de 6 bästa till matematik-VM eller IMO, som det egentligen heter. Jag blev imponerad av de senaste resultaten, då Sverige tog hem en
A Mathematician's Lament och allt som är fel med matematikundervisningen i skolan
![]()
Det är inte eleverna som är dålig och inte heller är det lärarnas fel att "matematiken" inte går in i elevernas hjärnor. Titta istället på kursplanerna för dagens mattekurser och försök att motivera varför vi på 2000-talet ska lära ut
Problem om att ta sig över till andra sidan

Året var 1997. Det var då jag började ha matematiska framgångar och blev därmed skickad på en resa till den stora staden Moskva. Där skulle jag och andra 6:or och 7:or tävla i problemlösning. Som jag minns det gick det hyfsat ok för mig, men ett
Finns det något liv efter "Prinsessan eller tigern?"
![]()
"Prinsessan eller tigern?" är en matematisk novell av Raymond Smullyan. Ni kan läsa berättelsen i sin helhet här på bloggen, inklusive svaren på gåtorna.
Prinsessan eller tigern? - Dag 1
Prinsessan eller tigern? - Dag 2
Prinsessan eller tigern?
Fibonaccitalen och gyllene snittet
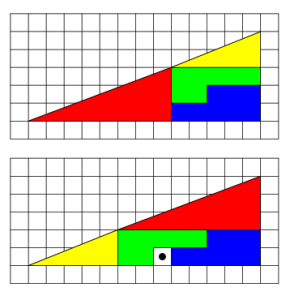
Ett välkänt trick är att man kan klippa en triangel i bitar, arrangera om bitarna, sätta ihop dem till en triangel igen och få en extra ruta!
Hur kan det stämma? Nedan kommer förklaringen, men fundera själv
Andra vinnarna i tävlingen vårterminen 2011
Ni läsarna har sagt ert, vilket resulterar i att bidrag 5 och bidrag 6 vinner tävlingen för snyggast lösning.
Det vill säga vinnarna den här våren (förutom Skägget) är Benjamin och David! Grattis, priserna ska jag skicka ut i augusti!
För min
Filmtitlar

Rebusarna motsvarar filmtitlar på engelska. Försök att lista ut så många du
Lösningar, som vi väljer - del 2
![]()
Den här matematiska sagan är skriven av Victor Ufnarovski och publiceras här med hans tillåtelse.
Stabila äktenskap
"Idag började vi vår långa rymdfärd", inledde kaptenen på den första rymdflygningen "Jorden-Andromeda" sitt anförande. "Ni vet
Trollekvation
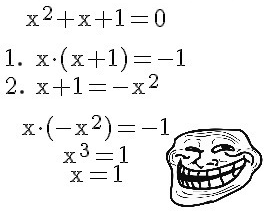
Låt oss lösa en andragradsekvation. Vi gör det inte med hjälp av pq-formeln utan på ett annat
Problem vecka 21
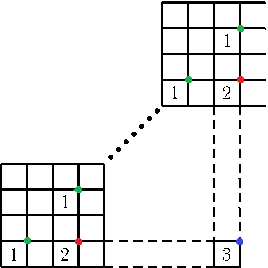
Matchen (2 poäng).
Innan fotbollsmatchen mellan lag Syd och lag Nord fanns det 5 prognoser:
a) det kommer inte att bli oavgjort
b) Syd kommer att släppa in mål
c) Nord kommer att vinna
d) Nord kommer inte att förlora
e) det kommer bli exakt 3
Problem vecka 20
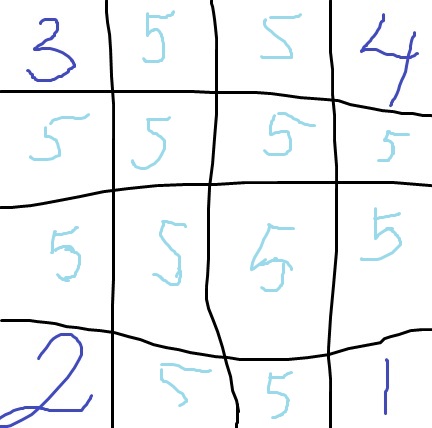
Cthulhu (1 poäng).
"Ni alledels för små för att se detta", sade Cthulhu till sina 33 barn och skrek ut "Blunda!". Alla pojkarna blundade med högerögat, likaså en tredjedel av flickorna. Alla flickorna blundade med vänsterögat, likaså en tredjedel
Lösningar, som vi väljer - del 1
![]()
Den här matematiska sagan är skriven av Victor Ufnarovski och publiceras här med hans tillåtelse.
Vi måste välja. Vi måste fatta beslut. Vi gör det varje dag. Och beklagar ibland hela livet. . .
Men man måste veta att det finns några
Problem vecka 19
![]()
Uttrycket (3 poäng).
Man utvecklade uttrycket (x+y)^n med hjälp av binomialsatsen. Den andra termen i summan blev lika med 240, den tredje blev lika med 720 och den fjärde blev lika med 1080. Hitta x, y och n.
Ön (7 poäng).
a) På en platt
Prinsessan eller tigern? Dag 4 (den sista dagen)
![]()
Den här interaktiva berättelsen har skrivits av Raymond Smullyan och ingår i boken "The Lady or the Tiger?" Översättningen till svenska är min egen.
Notera att "eller" är matematiskt ("A eller B" är sant även ifall både A och B är sant), likaså
Problem vecka 18
![]()
Cirkelkonstruktion (2 poäng).
Du har en passare, som du kan rita cirklar med (så länge du känner till cirkelns mittpunkt och dess radie) samt en ograderad linjal, som du inte kan mäta något med, men som du kan rita en linje med genom två valfria
Problem vecka 17
![]()
Nötter (1 poäng).
I tre högar finns 22, 14 respektive 12 nötter. Du får göra tre förflyttningar, så att högarna får lika många nötter. Under en förflyttning får du flytta ett antal nötter från en hög till en annan, men antalet nötter man flyttar
Problem vecka 16
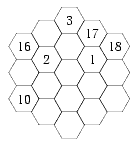
Hexagonen (1 poäng).
Fyll i rutorna i "hexagonen" nedan med heltalen från 1 till 19, så att summan av talen i varje kolonn och i varje diagonal blir densamma. Varje tal får utnyttjas exakt en gång, och vissa tal är redan på sin
Prinsessan eller tigern? Dag 3
![]()
Den här interaktiva berättelsen har skrivits av Raymond Smullyan och ingår i boken "The Lady or the Tiger?" Översättningen till svenska är min egen.
Gå till första kapitlet
Dag 3
“Attans”, utropade kungen, “även denna gång kom alla fångar iväg!
Problem vecka 15
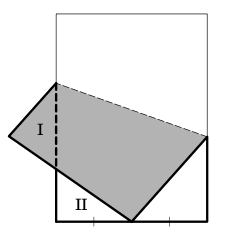
Papper (3 poäng).
Man tog ett rektangulärt papper och vikte ihop det så att ena hörnet hamnade i mitten på kortsidan (se bilden). Det visade sig att trianglarna I och II var kongruenta.
Hur lång var papprets långsida om kortsidan var 8 cm
Tangent
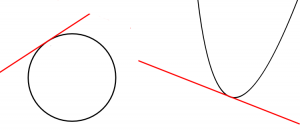
När jag säger "tangentlinje" tänker du kanske på någon av dessa bilder:
En tangentlinje nuddar precis en kurva i en viss punkt. Ofta har jag tänkt att en tangent aldrig är en sekant, det vill säga att tangenten aldrig kan skära kurvan.
Men
Problem vecka 14
![]()
Fången (2 poäng).
Kungen tänker på tre stycken tvåsiffriga tal: a, b och c. Fången måste hitta på tre tal själv och säga dem högt: X, Y och Z. Därefter säger kungen högt summan aX+bY+cZ. Då måste fången gissa rätt på vilka tre tal kungen tänkte
Problem vecka 13
![]()
Kaniner (1 poäng).
En kaninmamma köpte 7 olika stora trummor och 7 olika stora trumpinnar-set åt sina 7 kaninbarn. Om en kanin ser att någon av syskonen har både mindre trumma och mindre trumpinnar, börjar den slå på trumman väldigt högt. Annars
Problem vecka 12
![]()
Syskon (1 poäng). I en familj finns sex barn. Fem av barnen är 2, 6, 8, 12 respektive 14 år äldre än det minsta barnet. Alla åldrarna i familjen är primtal. Hur gammalt är det minsta barnet?
Primtal
Ett primtal är ett positivt heltal som har exakt
Problem vecka 11
Nu kommer de svåraste problemen hittills! Nästa vecka återkommer jag till normal svårighetsgrad.
Skicka in lösningsförslag genom att klicka på länken under uppgifterna senast måndagen den 28 mars. Glöm inte att kolla reglerna och aktuella
Prinsessan eller tigern? Dag 2
![]()
Den här interaktiva berättelsen har skrivits av Raymond Smullyan och ingår i boken "The Lady or the Tiger?" Översättningen till svenska är min egen.
Gå till första kapitlet
Dag 2
"Igår gjorde vi bort oss", sade kungen till sin rådgivare, "alla
Problem vecka 10
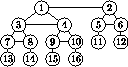
Skicka in lösningsförslag genom att klicka på länken under uppgifterna senast måndagen den 21 mars. Glöm inte att kolla reglerna och aktuella poängställningen.
Blommor (2 poäng). Längs med vägen mellan Kalles och Kajsas stugor växte blommor på
Ovanlig sudoku
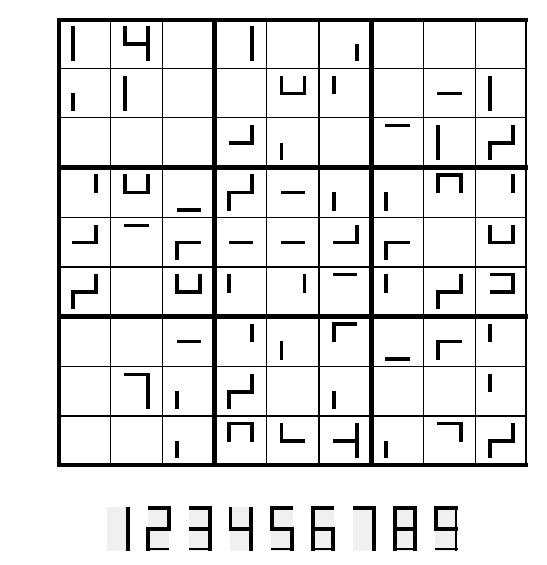
Försök att lösa! Som vanligt ska varje stor ruta, varje rad och varje kolumn innehålla alla 9 siffrorna en gång
Problem vecka 9
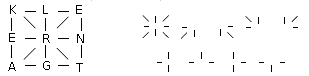
Skicka in lösningsförslag genom att klicka på länken under uppgifterna senast måndagen den 14 mars. Glöm inte att kolla reglerna och aktuella poängställningen.
Rebusen (1 poäng). Försök att läsa av ordet genom att använda
Prinsessan eller tigern? Dag 1
![]()
Den här interaktiva berättelsen har skrivits av Raymond Smullyan och ingår i boken "The Lady or the Tiger?" Översättningen till svenska är min egen.
Frank R. Stockton skrev en saga som heter “Prinsessan eller tigern?”. I sagan måste en fånge
Problem vecka 8. Tävlingsstart!

Kuben (1 poäng). En träkub har sidlängden 1 m. Vi sågar upp kuben i små kuber som alla har sidlängden 1 cm och lägger alla småkuberna på en rad. Hur lång blir raden?
Siffertriangeln (3 poäng). Går det att fylla de gula cirklarna med siffrorna
Lektion om potenser

Baserat på första lektionen, har jag gjort en presentation om potenser. Drygt hälften av föredraget kommer från den första lektionen jag lade upp, men resten är utfyllt med mer material om potenser. Se för er själva!
Lektion om potenser - tog
Adventsgåtorna besvarade
![]()
Nu har alla decembergåtor fått svar!
Jag vill tacka alla läsarna som påpekat oklarheter och felaktigheter i svar. Fortsätt gärna att göra så!
Här är alla adventsgåtorna:
Pappersark
Sifferrebus
Myntpåsar
Läskig sjukdom
Klurigt
HMT-final 2011
![]()
I lördags genomfördes den årliga finalen av Högstadiets Matematiktävling, där Sveriges 44 bästa högstadieelever deltog. Jag var på plats i min gamla gymnasieskola (Danderyds Gymnasium) och såg bl.a. på prisutdelningen.
Jag vill säga ett stort
En möbiussaga

En vän tipsade mig om den här fina sagan:
Historian kommer från användaren Vihart på Youtube, som har andra underbara videor. Jag har sett serien "Doodling in Math" och känt igen mig väldigt mycket
Lektioner i matte C
![]()
Ett nytt år innebär för mig nya sysselsättningar. Vårterminen 2011 blev jag nämligen för första gången en gymnasielärare!
Jag undervisar en grupp elever i matte C på ett gymnasium i Uppsala och det är då andra halvan av kurser som gäller för min
Adventspyssel 24

.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;
Adventspyssel 23

.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;
Adventspyssel 22
.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;
Adventspyssel 21
.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;
Adventspyssel 20
![]()
.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;
Adventspyssel 19
.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;
Adventspyssel 18

.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;
Adventspyssel 17
![]()
.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;
Adventspyssel 16
![]()
.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;
Adventspyssel 15
![]()
.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;
Adventspyssel 14
.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;
Adventspyssel 13
.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;
Adventspyssel 12

.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;
Adventspyssel 11
.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;
Vinnare bland yngre ht 2010!
![]()
.vinnareht10 {
padding: 5px 5px; border: 5px solid #e7db1b; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px; width: 400px; align: center;
}
Ram badapadam! Terminens tävling för de yngre är
Adventspyssel 10
![]()
.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;
Lösningen till problemet för de yngre vecka 47
![]()
.problemly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.problemlly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px
Adventspyssel 9

.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;
Vinnare bland äldre ht 2010!
![]()
.vinnareht10 {
padding: 5px 5px; border: 5px solid #e7db1b; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px; width: 400px; align: center;
}
Pam padadam! Terminens tävling för de äldre
Adventspyssel 8
![]()
.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;
Lösningen till problemet för de äldre vecka 47
![]()
.problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 10px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;
Adventspyssel 7
![]()
.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;
Adventspyssel 6
![]()
.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;
Adventspyssel 5

.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px
Adventspyssel 4
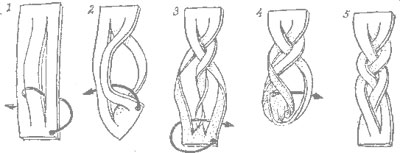
.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px
Adventspyssel 3
![]()
.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px
Lösningen till problemet för de yngre vecka 46
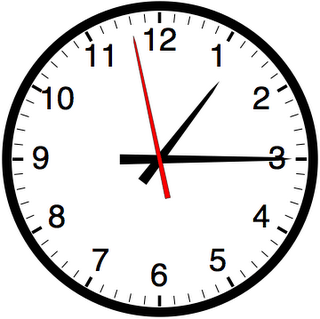
.problemly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.problemlly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px
Adventspyssel 2
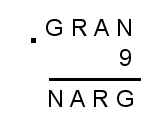
.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px
Adventspyssel 1
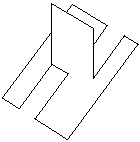
.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px
Lösningen till problemet för de äldre vecka 46
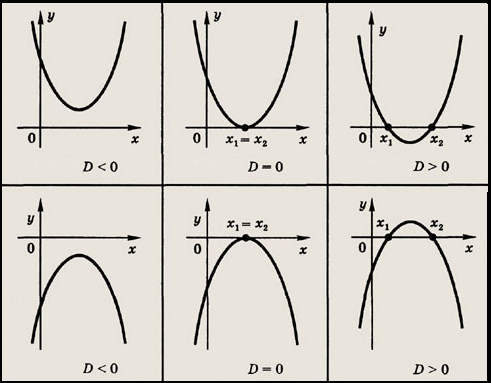
.problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 10px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;
HMT-kval 2010
![]()
Som traditionen är, rättar elever som gått på Danderyds Gymnasium tävlingen HMT varje år. Även elever som gick ut gymnasiet för mer än 6 år sedan...
I helgen rättade vi alla inskickade bidrag och jag fick äran att vara med och rätta uppgift nummer
Matteproblem för de yngre vecka 47
![]()
.problemy45 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #BBEE99; -moz-border-radius: 10px; border-radius: 10px;
}
.equation {
padding: 0px 0px; border: 3px solid #526B7F;
}
Lösningen till problemet för de yngre vecka 45

.problemly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.problemlly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px
Matteproblem för de äldre vecka 47
![]()
.problema45{
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #B2DCFF; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;
Lösningen till problemet för de äldre vecka 45

.problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 10px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;
Svenska skolböcker
![]()
Som privatlärare börjar jag sätta mig in i de svenska matteböckernas värld. Själv gick jag bara ett år på svenska högstadiet och då fick jag hålla på med egna matteböcker.
Skillnaderna i 5:ans mattebok och 8:ans mattebok vad gäller pedagogiken är
Matteproblem för de yngre vecka 46
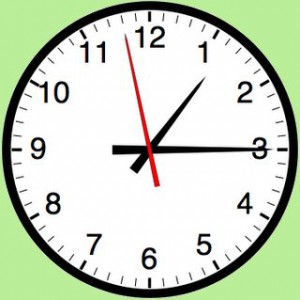
.problemy45 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #BBEE99; -moz-border-radius: 10px; border-radius: 10px;
}
.equation {
padding: 0px 0px; border: 3px solid #526B7F;
}
Lösningen till problemet för de yngre vecka 44
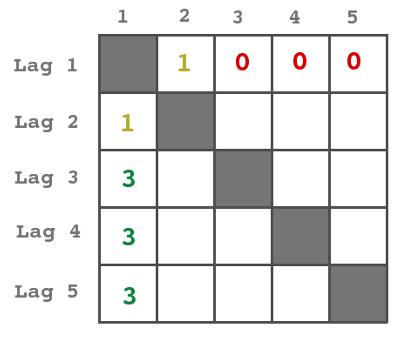
.problemly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.problemlly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px
Matteproblem för de äldre vecka 46
![]()
.problema45{
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #B2DCFF; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;
Lösningen till problemet för de äldre vecka 44
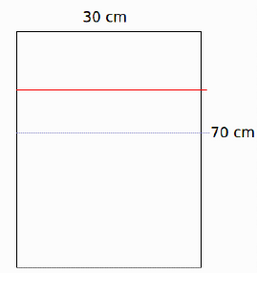
.problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 10px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;
Lösningar till Sonja Kovalevsky-dagarnas problem 2010
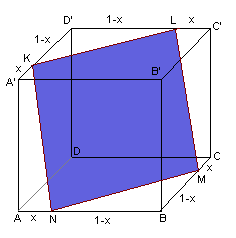
Äntligen är de här, lösningarna till problemen som eleverna tävlade i under Sonja Kovalevsky-dagarna 2010!
Lösningar till alla 15
Sonja Kovalevsky-dagarna i Stockholm 2010

För tredje gången i rad var jag med och ordnade problemlösning (tillsammans med Dag Jonsson, Magnus Carlson och min pappa) på Sonja Kovalevsky-dagarna. Tredje gånget gillt verkar det som.
Dessa dagar har som syfte att visa varför det är bra
Matteproblem för de yngre vecka 45

.problemy45 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #BBEE99; -moz-border-radius: 10px; border-radius: 10px;
}
.equation {
padding: 0px 0px; border: 3px solid #526B7F;
}
Lösningen till problemet för de yngre vecka 43
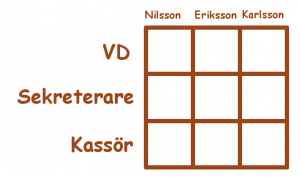
.problemly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.problemlly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px
Matteproblem för de äldre vecka 45

.problema45{
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #B2DCFF; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;
Lösningen till problemet för de äldre vecka 43

.problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 10px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;
Kombinatorik i Futurama

En mörk eftermiddag hade ett gäng studenter samlats för att kolla på - ni gissade rätt - Futurama! Ljuset släcktes, stora platt-teven
Matteproblem för de yngre vecka 44

.problemy44 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #BBEE99; -moz-border-radius: 10px; border-radius: 10px; height: 180px;
}
.equation {
padding: 0px 0px; border: 3px solid #526B7F;
}
Lösningen till problemet för de yngre vecka 42
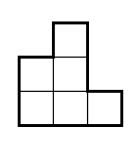
.problemly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.problemlly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px
Matteproblem för de äldre vecka 44

.problema44{
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #B2DCFF; -moz-border-radius: 10px; border-radius: 10px; height: 220px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0
Lösningen till problemet för de äldre vecka 42
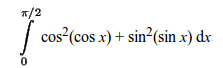
.problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 10px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;
Matteproblem för de yngre vecka 43

.problemy42 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #BBEE99; -moz-border-radius: 10px; border-radius: 10px;
}
.equation {
padding: 0px 0px; border: 3px solid #526B7F;
}
Lösningen till problemet för de yngre vecka 41
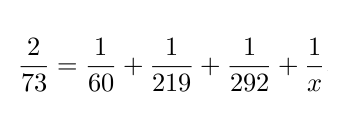
.problemly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.problemlly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px
Matteproblem för de äldre vecka 43
![]()
.problem{
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #B2DCFF; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;
Lösningen till problemet för de äldre vecka 41

.problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 10px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;
Matteproblem för de yngre vecka 42

.problemy42 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #BBEE99; -moz-border-radius: 10px; border-radius: 10px;
}
.equation {
padding: 0px 0px; border: 3px solid #526B7F;
}
Lösningen till problemet för de yngre vecka 40
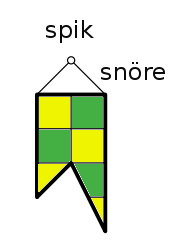
.problemly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.problemlly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px
Matteproblem för de äldre vecka 42
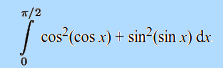
.problem{
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #B2DCFF; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;
Lösningen till problemet för de äldre vecka 40
![]()
.problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 10px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;
SMT-rättningskonferens
![]()
Lite oväntat fick jag i år vara med och rätta Skolornas Matematiktävling, den riksomfattande matematiktävlingen för gymnasiet.
Rättningskonferensen var nämligen i Uppsala i år och tävlingens komittét behövde hjälp med rättningen, ty antalet
Matteproblem för de yngre vecka 41
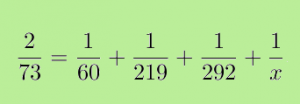
.problemy41 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #BBEE99; -moz-border-radius: 10px; border-radius: 10px; height: 200px;
}
.equation {
padding: 0px 0px; border: 3px solid #526B7F;
}
Lösningen till problemet för de yngre vecka 39
![]()
.problemly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.problemlly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px
Matteproblem för de äldre vecka 41
![]()
.problem{
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #B2DCFF; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;
Lösningen till problemet för de äldre vecka 39

.problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 10px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;
Matteproblem för de yngre vecka 40
.problemy36 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #BBEE99; -moz-border-radius: 10px; border-radius: 10px; height: 180px;
}
Mattegåta
En man har ett litet hål i väggen (lika stor som
Lösningen till problemet för de yngre vecka 38
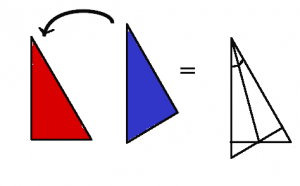
.problemly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.problemlly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px
Matteproblem för de äldre vecka 40
![]()
.problem{
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #B2DCFF; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;
Lösningen till problemet för de äldre vecka 38
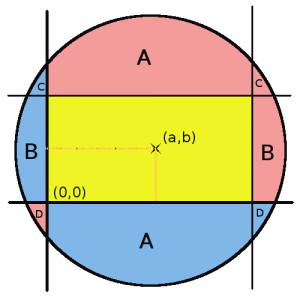
.problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 10px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;
Matematikerns klagan
![]()
Vad vore matematiken utan bevis?
Inte riktig matematik, tycker många och artisten Skägget håller med, när han sitter och lider igenom kursen i Sannolikhet och statistik.
Hans senaste låtkreation heter Matematikerns klagan och är en kampsång för
Matteproblem för de yngre vecka 39
![]()
.problemy36 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #BBEE99; -moz-border-radius: 10px; border-radius: 10px;
}
Mattegåta
Pippi, Tommy och Annika delar på 100 godisbitar. Det är Pippi
Lösningen till problemet för de yngre vecka 37
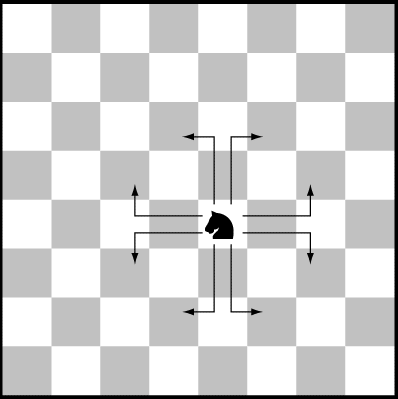
.problemly37 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px; height: 640px;
}
.problemlly37 {
padding: 5px 5px; border: 5px solid #526B7F;
Matteproblem för de äldre vecka 39

.problem{
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #B2DCFF; -moz-border-radius: 10px; border-radius: 10px;
}
MattegåtaPå en gata finns två radhus och i varje radhus bor två djurgalna
Lösningen till problemet för de äldre vecka 37

.problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 10px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;
Planära grafer
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;
margin-bottom: 10px; background: url(http://mattebloggen.com/wp-content/uploads/2010/09/satsbakgrund1.png) repeat; -moz-border-radius: 10px; border-radius: 10px; width:
Matteproblem för de yngre vecka 38
![]()
.problemy36 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #BBEE99; -moz-border-radius: 10px; border-radius: 10px;
}
Mattegåta
Jon-Erik har en triangel utan några markeringar, som är gjord
Lösningen till problemet för de yngre vecka 36

.problemly36 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px; height: 180px;
}
.problemlly36 {
padding: 5px 5px; border: 5px solid #526B7F;
Matteproblem för de äldre vecka 38
![]()
.problem{
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #B2DCFF; -moz-border-radius: 10px; border-radius: 10px;
}
MattegåtaEn cirkel är ritad på koordinatplanet och dess mittpunkt har
Lösningen till problemet för de äldre vecka 36
![]()
.problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 10px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;
Skolornas matematiktävling
Skolornas matematiktävling är den officiella mattetävlingen vi har för gymnasister i Sverige.
Förutom att att tävla i matte är jätteroligt, kan dina resultat också ge meritpoäng vid antagning på universitet/högskola, både som student och
Matteproblem för de yngre vecka 37

.problemy36 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #BBEE99; -moz-border-radius: 10px; border-radius: 10px;
}
MattegåtaEn springare hoppar alltid på schackbrädet antingen två rutor
Lösningen till problemet för de yngre vecka 35
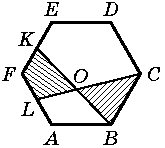
.problemy351 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; height: 200px; -moz-border-radius: 10px; border-radius: 10px;
}
.problemy352 {
padding: 0px 5px; border: 5px solid #526B7F;
Matteproblem för de äldre vecka 37
![]()
.problem {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #B2DCFF; -moz-border-radius: 10px; border-radius: 10px;
}
Mattegåta Fredrik och Mona har 1999 kronor i kontanter tillsammans och ingen
Lösningen till problemet för de äldre vecka 35

.problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
Mattegåta Hitta det största antalet kongruenta icke-konvexa polygoner som man
Matteproblem för de yngre vecka 36

.problemy36 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #BBEE99; -moz-border-radius: 10px; border-radius: 10px;
}
MattegåtaGissa vilken symbol som ska stå istället för frågetecknet i den
Lösningen till problemet för de yngre vecka 34

.problemy34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
Mattegåta Hitta två äkta bråk, det ena med nämnaren 8 och det andra med
Videohjälp
![]()
Som prenumerant på Nyhetsbrev matematik från skolverket har jag stött på nyheten om Fröken Matte som tydligen gjort succe på YouTube. Det är en fröken från Hagagymnasiet i Borlänge som har lagt upp videor som behandlar matte B på nätet. Alla
Matteproblem för de äldre vecka 36
![]()
.problem {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #B2DCFF; -moz-border-radius: 10px; border-radius: 10px;
}
Mattegåta Ekvationen x2+px+q=0 har bara heltalsrötter och man vet att både p och
Lösningen till problemet för de äldre vecka 34
![]()
.problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
Mattegåta Låt a^b beteckna talet a upphöjt till talet b. Man skall sätta ut
Matteproblem för de yngre vecka 35

Mattegåta Cissi fyllde år så hon bakade en tårta till sin födelsedag. Tårtan var dock inte rund, utan formad som en regelbunden sexhörning ABCDEF. Cissi markerade K och L, som var mittpunkterna på sidorna EF och FA respektive. Sedan skar hon längs
Matteproblem för de äldre vecka 35
![]()
.problem {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #B2DCFF; -moz-border-radius: 10px; border-radius: 10px;
}
Mattegåta Hitta det största antalet kongruenta icke-konvexa polygoner som man
Matteproblem för de yngre vecka 34
![]()
.problemy {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #BBEE99; -moz-border-radius: 10px; border-radius: 10px;
}
Mattegåta Hitta två äkta bråk, det ena med nämnaren 8 och det andra med
Matteproblem för de äldre vecka 34
![]()
.problem {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #B2DCFF; -moz-border-radius: 10px; border-radius: 10px;
}
Mattegåta Låt a^b beteckna talet a upphöjt till talet b. Man skall sätta ut
Lektioner från kollot

Snart är sommaren slut för min del och det är dags att sammanfatta vad jag lärt mig under mattekollotiden (jag var lärare för några av Rysslands mest skärpta åttor):
1. Åttan är lite för tidig årskurs för att introducera begreppet grupp.
2.
Lösning till problem vecka 23
![]()
En tärning låg på bordet. Den flyttades ett steg i taget genom att rullas över på en ny sida (som gränsade till sidan som nyss var i kontakt med bordet). Till slut hamnade tärningen på samma plats som i början med samma sida uppåt. Kunde den översta
Lösning till problem vecka 22
![]()
Det finns två potatisar med godtycklig form och storlek. Visa att man kan lägga på var sin bit koppartråd på deras ytor så att det bildas två böjda ringar (inte nödvändigtvis platta), som har samma form och storlek.
Erik T. förser oss med lösningen
Klassiska bevis: Randvinkelsatsen
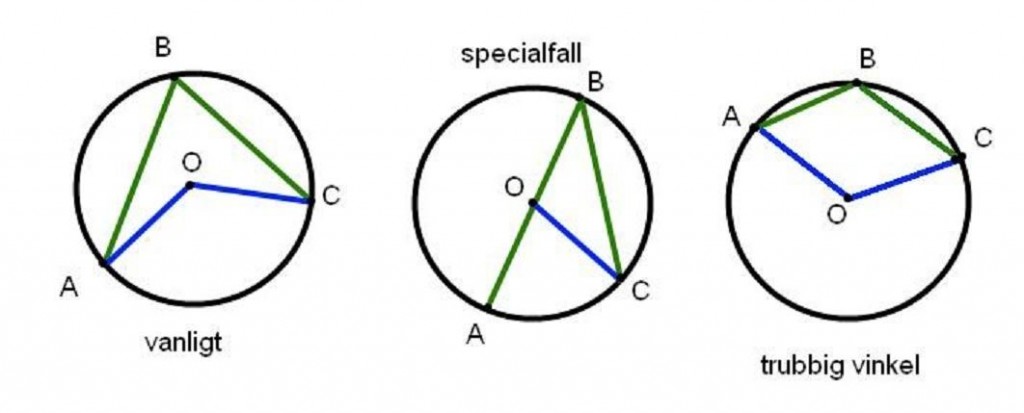
Många har hört talas om den beryktade randvinkelsatsen. Eventuellt har du träffat på den på gymnasiet. Men få har egentligen koll på hur man bevisar satsen.
Om du vill komma fram till beviset själv med hjälp av några ledande uppgifter, se Cirklar
Matteproblem vecka 23

En tärning låg på bordet. Den flyttades ett steg i taget genom att rullas över på en ny sida (som gränsade till sidan som nyss var i kontakt med bordet). Till slut hamnade tärningen på samma plats som i början med samma sida uppåt. Kunde den översta
Lösning till problem vecka 21
![]()
På dataskärmen står ett tal, som varje minut ökar med 102. Från början står det 123. Programmeraren Daniel kan när som helst ändra ordningen på siffrorna i talet på dataskärmen. Kan han garantera att talet aldrig blir fyrsiffrigt?
Lösning:
Jadå,
Den bästa låten om ringar
![]()
Jag är stolt över att få presentera låten, som redan är känd för många matematikstuderande vid Uppsala Universitet.
Texten är baserad på innehållet i kursen Algebra II, där mycket ringteori ingår.
Låten heter just Ringteori och stilen är
Transformationsmatrisen - del 5
![]()
Från Transformationsmatrisen – del 4 fick vi följande resultat:
För att bestämma transformationsmatrisen från bas $$A$$ till bas $$B$$, uttryck basvektorerna i basen $$B$$ och skriv in resultaten som kolonner i en matris.
Hur gör man då det
Matteproblem vecka 22
![]()
Det finns två potatisar med godtycklig form och storlek. Visa att man kan lägga på var sin bit koppartråd på deras ytor så att det bildas två böjda ringar (inte nödvändigtvis platta), som har samma form och
Lösning till problem vecka 20
![]()
På ett lager fanns likadana ostar. En natt kom sluga råttor dit och åt upp 10 av ostarna. Varje råtta åt lika mycket. Några råttor klarade dock inte av måltiden och fick ont i magen. Nästa natt kom de 7 råttorna som inte fick ont i magen och åt upp
Matteproblem vecka 21

På dataskärmen står ett tal, som varje minut ökar med 102. Från början står det 123. Programmeraren Daniel kan när som helst ändra ordningen på siffrorna i talet på dataskärmen. Kan han garantera att talet aldrig blir
Lösning till problem vecka 19
![]()
En fotboll är hopsydd av 32 lappar: vita sexkanter och svarta femkanter. Varje svart lapp gränsar till bara vita, varje vit lapp gränsar till tre vita och tre svarta lappar. Hur många vita lappar finns det i en fotboll?
Man kan anta att
Matteproblem vecka 20

På ett lager fanns likadana ostar. En natt kom sluga råttor dit och åt upp 10 av ostarna. Varje råtta åt lika mycket. Några råttor klarade dock inte av måltiden och fick ont i magen. Nästa natt kom de 7 råttorna som inte fick ont i magen och åt
Matteproblem vecka 19

En fotboll är hopsydd av 32 lappar: vita sexkanter och svarta femkanter. Varje svart lapp gränsar till bara vita, varje vit lapp gränsar till tre vita och tre svarta lappar. Hur många vita lappar finns det i en
Lösning till problem vecka 18
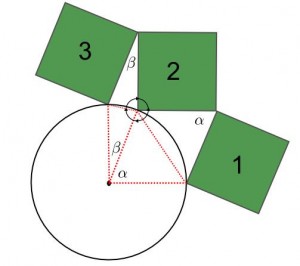
På bordet ligger en papperscirkel med radien 5 cm. Så länge det är möjligt, lägger Ilian till papperskvadrater med sidan 5 cm intill cirkeln så att följande villkor uppfylls:
1. Varje kvadrat har ett hörn som nuddar cirkeln.
2. Kvadraterna
Lösning till problem vecka 17
![]()
En och samma fredagsfilm startade samtidigt på två televisionskanaler. Ena kanalen delade upp filmen i stycken om 20 minuter och sände 2 minuter långa reklampauser mellan filmstycken. Den andra kanalen delade upp filmen i 10 minuters-stycken och
Inför IMO 2010

Härmed vill jag gratulera min mattecirkelelev, Benjamin Fayyazuddin-Ljungberg, för att han har blivit utvald till det svenska laget i tävlingsmatematik!
Tillsammans med 5 andra gymnasister kommer han att representera Sverige i den 51:a
Transformationsmatrisen - del 4
![]()
Vi vill göra livet så enkelt som möjligt för oss. Så vi räknar ut transformationsmatrisen som på det andra sättet i Transformationsmatrisen - del 3.
Vi kollar först på ett lite större exempel. Låt oss räkna ut transformationsmatrisen mellan baserna
Matteproblem vecka 18
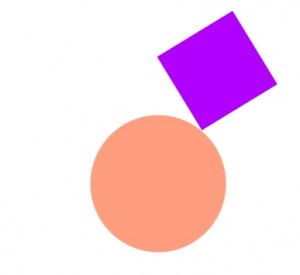
På bordet ligger en papperscirkel med radien 5 cm. Så länge det är möjligt, lägger Ilian till papperskvadrater med sidan 5 cm intill cirkeln så att följande villkor uppfylls:
1. Varje kvadrat har ett hörn som nuddar cirkeln.
2. Kvadraterna
Lösning till problem vecka 16
![]()
Thomas skrev ner alla dagar i en viss månad på en rad: 123456789101112... Sedan målade han över 3 av dagarna (som var hans kompisars födelsedagar) och inga övermålade dagar var precis efter varandra. Det visade sig att alla omålade områden består av
Matteproblem vecka 17

En och samma fredagsfilm startade samtidigt på två televisionskanaler. Ena kanalen delade upp filmen i stycken om 20 minuter och sände 2 minuter långa reklampauser mellan filmstycken. Den andra kanalen delade upp filmen i 10 minuters-stycken och
Lösning till problem vecka 15
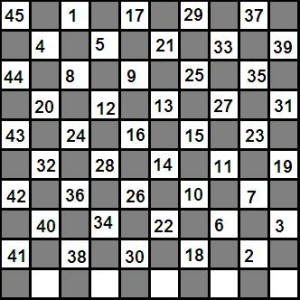
På ett 10x10-bräde finns en pjäs i varje ruta. En tillåten operation är att välja en diagonal som innehåller ett jämnt antal pjäser och ta bort en valfri pjäs från den diagonalen. Hur många pjäser kan man som mest ta bort med hjälp av sådana
Matteproblem vecka 16

Thomas skrev ner alla dagar i en viss månad på en rad: 123456789101112... Sedan målade han över 3 av dagarna (som var hans kompisars födelsedagar) och inga övermålade dagar var precis efter varandra. Det visade sig att alla omålade områden består av
Lösning till problem vecka 14
Eli och Tiffany är kompisar och bor i grannhus. Eli bor på nummer 4. Om Tiffany ska ta den kortaste vägen till Eli, så spelar det ingen roll på vilken sida hon springer runt hennes eget hus. Bestäm numret som Tiffany bor på.
Lösning:
Om
Transformationsmatrisen - del 3
![]()
Det här är fortsättningen på inläggen Transformationsmatrisen - del 1 och Transformationsmatrisen - del 2. I de två första delarna behandlades begreppen bas och vektorernas koordinater i olika baser.
Hur bestämmer man en
Matteproblem vecka 15
![]()
På ett 10x10-bräde finns en pjäs i varje ruta. En tillåten operation är att välja en diagonal som innehåller ett jämnt antal pjäser och ta bort en valfri pjäs från den diagonalen. Hur många pjäser kan man som mest ta bort med hjälp av sådana
Matteproblem vecka 14

Eli och Tiffany är kompisar och bor i grannhus. Eli bor på nummer 4. Om Tiffany ska ta den kortaste vägen till Eli, så spelar det ingen roll på vilken sida hon springer runt hennes eget hus. Bestäm numret som Tiffany bor
Hissen
Rekommenderad från: 12 år
[kkratings]
Eli bor i ett höghus med 9 våningar. Han kan åka hiss från sin egen våning till den första och då tar det 1 minut.
Men han når inte knappen till sin egen våning, eftersom han är så liten. Istället trycker
Ett falskt mynt

Rekommenderad från: 13 år
[kkratings]
Du har hittat en skatt som består av 6 stycken antika mynt. I skattkistan låg en lapp som berättade om att ett av mynten är falskt. Det väger inte lika mycket som de riktiga mynten (de riktiga mynten väger
Transformationsmatrisen - del 2
Det här är fortsättningen på inlägget Transformationsmatrisen - del 1. I första delen behandlas begreppet baser.
Vektorer i olika baser
Vektorer som skrivs med hjälp av siffror till exempel så här $$\left(\begin{array}{c}
\sqrt{2}
Transformationsmatrisen – del 1
De flesta matematik- och ingenjörsstudenter läser någon form av linjär algebra. Det är ett högst rimlig inslag i deras utbildning - vilken vuxen människa räknar inte med matriser :)?
Just beräkningar är dessutom det studenterna måste lära sig
Fler rektanglar
Rekommenderad från: 11 år
[kkratings]
Pelle delade upp ett 8x8-bräde i 30 stycken rektanglar på så sätt att likadana rektanglar inte nuddar varandra, inte ens med hörn. Försök att förbättra hans resultat genom att dela upp brädet i ännu
Familjefika
![]()
Rekommenderad från: 12 år
[kkratings]
Under familjefikat drack alla en hel kopp kaffe med mjölk. Det visade sig att Terese drack en fjärdedel av all mjölk och en sjättedel av allt kaffe. Hur många familjemedlemmar finns det?
Visa
Liksidiga trianglar?
Rekommenderad från: 15 år
[kkratings]
Mattebloggen har en inofficiell tävling i att lösa matematikproblem. Skicka in din lösning med motivering till valentina.chapovalova@gmail.com, så har du chansen att vara med på topplistan. Har du någon
Dela upp kvadrater

Rekommenderad från: 12 år
[kkratings]
Kan man dela upp en kvadrat i 9 kvadrater och måla en av dem i vitt, 3 av dem i grått och 5 av dem i svart på så sätt att kvadrater med samma färg har samma storlek, men kvadrater med olika färg har
Alver och dvärgar
![]()
Rekommenderad från: 11 år
[kkratings]
I Skogsmården bor bara alver och dvärgar. Dvärgarna ljuger varje gång de pratar om sitt guld, annars talar de sanning. Alverna ljuger varje gång de pratar om dvärgar, annars talar de sanning. En gång
Ostbitar
![]()
Rekommenderad från: 12 år
[kkratings]
Det finns 25 ostbitar. Går det alltid att välja en bit, skära den i två delar på så sätt att osten nu kan läggas i två kassar så att den uppskurna ostens delar hamnar i olika kassar och det finns lika
Nians tabell
![]()
Rekommenderad från: 15 år
[kkratings]
På en rad står tal, som är delbara med 9, i stigande ordning: 9, 18, 27, 36 och så vidare. Under varje tal står dess siffersumma.
(a) På vilken plats i andra raden ser vi först talet 81?
(b) Vad kommer
Höstens mattegåtetävling är över!

Under höstterminen kom gåtorna varje vecka och den som löster allra flest var Johan B. Här ser ni honom tillsammans med första priset:
Vinnaren bland studenter var Erik R. och bland högstadieelever var det Olle K., Hanna H., Jennifer U.-L.,
Större än 2000?
![]()
Rekommenderad från: 15 år
[kkratings]
Vilket är större:
$0^5-399^2(400^3+2\cdot 400^2+3\cdot 400+4)$$ eller $00$$?
Visa lösningen
Lösning:
Detta kan vi egentligen räkna ut med vilja, våld och vaselin och sedan se
Omslag till tavlan
Rekommenderad från: 14 år
[kkratings]
Det finns en platt kvadratisk tavla som är 1 dm x 1 dm stor. Vi säger att ett pappersark i form av en rektangel med area 2 dm2 är ett omslag om man kan slå in tavlan i pappret så att båda sidorna
Jafar i ett fängelse
Rekommenderad från: 11 år
[kkratings]
Aladdin vill sätta Jafar i ett fängelse som består av 4 rum och 3 smala gångar mellan rummen. I varje gång står en tjock och trött vakt lutandes mot en av väggarna. Varje gång Jafar går över
Roliga mattelänkar
![]()
Här är lite mattejulpyssel:
Crazy paper thing
Förvisso har jag sett videon innan, men återupptäckte den igår på Let's Play Math!, en trevligt matteblogg på
Snälla och elaka labyrinter

Rekommenderad från: 15 år
[kkratings]
Man kan ta ett schackbräde och göra en "labyrint" av det genom att sätta upp små väggar på några av de ställen där en svart ruta gränsar till en vit.
Kalla en labyrint snäll ifall en liten
Högstadiets matematiktävling, kvalet 09 är rättat
![]()
En lördag morgon samlades några underliga människor vid ingången till ett universitet. De hade valt att rätt matteprov ideellt en hel lördag förmiddag från och med klockan 9 istället för att sova gott i sängen.
Dessa människor är nuvarande och före
Omkastad stad
Rekommenderad från: 12 år
[kkratings]
Benny skrev upp namnet på sin hemstad och alla cykliska "förskjutningar" av det och fick tabell 1. Sedan ordnade han om namnen och skrev de i bokstavsordning i tabell 2 i
Hur använder människor matte i vardagen?
![]()
För ett tag sedan åkte jag tåg från Stockholm till Köpenhamn och i sätena bredvid fick jag trevliga medpassagerare. Så småningom nämnde jag att jag höll på med matte, varpå kvinnan jag satt med berättade att hon faktiskt använde sig av matte i sitt
Okänd sifferkod

Rekommenderad från: 12 år
[kkratings]
En sifferkod, som består av 7 olika siffror kallas för godkänd sifferkod. Man vet att ett kassaskåp har en viss okänd godkänd sifferkod.
Om man slår in någon godkänd kod och åtminstone en rätt
Minnesregler för trigonometri - del 2
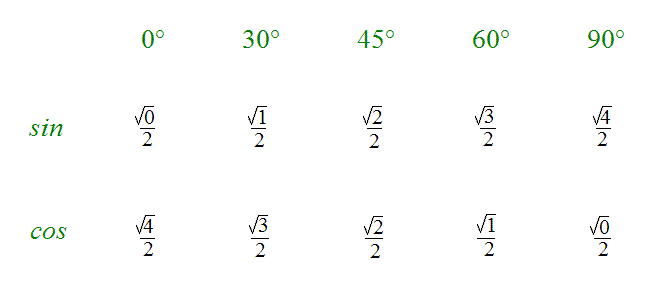
Det finns mängder med formler med sinus och cosinus att minnas, men inlärningsprocessen blir mycket lättare om man vet att de flesta utav formlerna är ganska lika.
Och så är det bra att komma ihåg att sinus är "snäll" och cosinus är "elak" (eller
Nästan kvadratisk figur
Rekommenderad från: 10 år
[kkratings]
Dela upp figuren på bilden i två sammanhängande delar, på så sätt att det går att sätta ihop delarna till en kvadrat 8*8.
Visa lösningen
Så här kan man
Hemliga uträkningar
![]()
Rekommenderad från: 15 år
[kkratings]
Robert tänker på två positiva tal: $$x$$ och $$y$$. Han skriver ner 4 tal på ett papper: $$x+y, x-y, xy$$ och $$\frac{x}{y}$$, men säger inte i vilken ordning han skriver ner dem. Hur kan Adam
Femtio tal
![]()
Rekommenderad från: 12 år
[kkratings]
Det finns femtio olika positiva heltal givna. Tjugofem av dem är inte större än 50 och resten är större än 50 men mindre än 100. Och inga två tal skiljer sig med exakt 50. Hitta summan av alla de
Fast på gräsmattan
Rekommenderad från: 14 år
[kkratings]
Fredrik står i mitten av en rund gräsmatta, som har radien 100 meter. Varje steg Fredrik tar är 1 meter långt. Varje gång han ska ta ett nytt steg anger han riktningen som han ska gå i. Anna har
Plan för staden med torg

Rekommenderad från: 12 år
[kkratings]
I en stad finns 6 torg. Ur varje torg utgår 3 raka vägar till exakt 3 andra torg. Inga två vägar korsar varandra. Bland de tre vägarna, som utgår från samma torg, ligger ena vägen inuti vinkeln,
Fyra färger räcker

Rekommenderad från: 14 år
[kkratings]
Det finns ett rutigt papper. På det finns rektanglar som har sin gräns gående längs med rutorna. Varje rektangel består av ett udda antal rutor och inga två rektanglar har gemensamma inre rutor.
Spiken i lådan
Rekommenderad från: 11 år
[kkratings]
Cissi klippte ut två likadana figurer ur en stor kartong. Sedan la hon dem på bottnen av en rektangulär låda så att de delvis täckte varandra. Det visade sig att hela bottnen blev täckt.
Sedan slog Kalle in en
Tvåpotensens sista siffra
![]()
Rekommenderad från: 15 år
[kkratings]
Det finns ett naturligt tal m, sådant att talet 2m har siffersumma 8. Kan sista siffran i talet 2m vara lika med 6?
Visa lösningen
Svar:
Det kan den inte! Jag har fått in tre stycken
Minnesregler för trigonometri - del 1
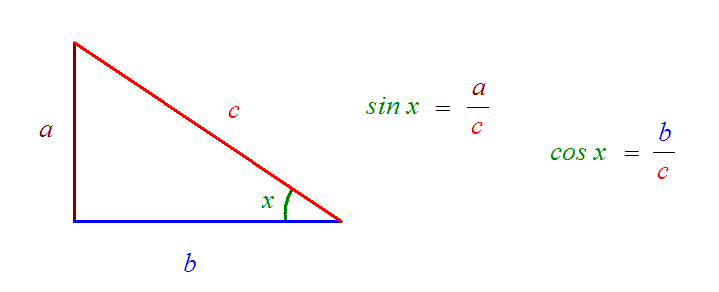
Det finns vissa saker som man bara måste lära sig utantill. Det kan tyckas att det är det enda som gäller i matten, men det kan räcka ganska långt att kunna bara några få formler.
Till exempel så kan vi prata om trigonometri. Jag tänkte dela med
Sabbad multiplikation
![]()
Rekommenderad från: 12 år
[kkratings]
På tavlan skrev matteläraren Adam en uträkning. Men precis innan lektionen skulle börja, så busade någon utav eleverna och bytte ut två siffror mot nya. Därefter stod
Kenken och set

För den som tröttnat på Sudoku och Battleships vill jag föreslå ett par andra pussel.
Den första är kenken, ett spel som självaste Gunnar Berg spenderar timmar med! Till synes liknar pusslet sudoku, men man får inte lika många siffror utsatta från
Grisarna och kexen

Rekommenderad från: 13 år
[kkratings]
Vargen bjöd hem de tre små grisarna och Rödluvan för att titta på film. Efter att de var klara gick Vargen till köket, räknade alla kex och upptäckte att det saknades två. Men han har en stor
Överstrykning med sex streck
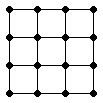
Rekommenderad från: 10 år
[kkratings]
Rita sex streck, så att alla 16 punkter på bilden blir överstrukna, utan att lyfta pennan från pappret och utan att strecken går längs med rutnätet.
Visa lösningen
Så här till
Mattecirkelns första träff

Första träffen på höstens mattecirkel äger rum på onsdagen den 2:a september kl. 15.20 i sal 169 på Katedralskolan i Uppsala. Alla nyfikna är välkomna! Det enda man behöver ha med sig är penna och
Klassiska bevis: Cevas sats, del 2
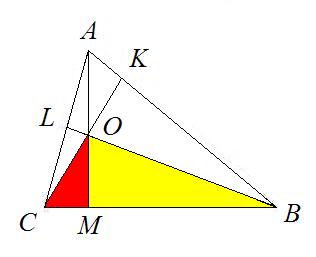
Detta inlägg är fortsättning på del 1 om Cevas sats. Första delen förklarar satsens formulering och ger tips för hur man skulle kunna bevisa den. Den här delen innehåller själva beviset.
Cevas sats
Given är en triangel ABC. Tre cevianer AM, BL
Klassiska bevis: Cevas sats, del 1
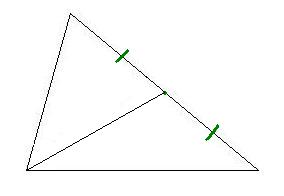
Cevas sats är ett av de vackraste geometriska faktum för trianglar. Men för att kunna formulera satsen lättare, ska vi först definiera vad en cevian är för något.
Cevianer
Medianen är ju en ganska känd sträcka, det är den som går ut från ett
Mattecirkel på Katedralskolan i höst

Jag är glad att annonsera nyheten: det kommer hållas en matematikcirkel för intresserade gymnasieelever i höst! Som bas kommer jag att ha Katedralskolan i Uppsala (alternativt rektorsvillan), men elever från alla skolor är givetvis välkomna.
Detta
Mattekollo

Ännu en juli har passerat då jag har jobbat som lärare på ett mattekollo. Det var en spännande månad med tonvis jobb och upplevelser.
Vi organiserade
Dyra uträkningar

Rekommenderad från: 12 år
[kkratings]
Använd valutan euro, mynt och sedlar, för att beteckna talen 1, 2, 5 och 10. Med hjälp av dem och (gratis) parenteser och de fyra räknetecken (+, -, *, /) bilda ett uttryck, vars värde är 2009,
En följd av fyrhörningar
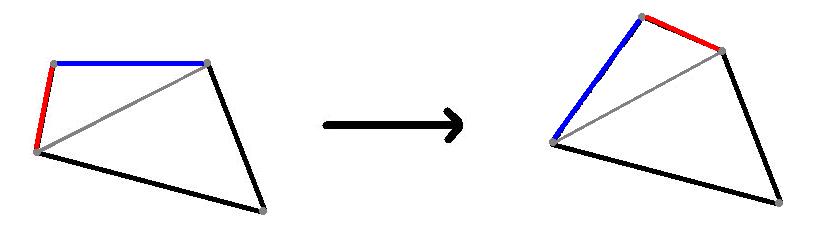
Rekommenderad från: 15 år
[kkratings]
Låt F1 vara en godtycklig konvex fyrhörning. För k>1, Fk konstrueras genom att man skär Fk-1 i två delar längs en av dess diagonaler, vänder på en av delarna och sedan klistrar delarna samman längs
Ljug när du föreläser
![]()
Bra fysikföreläsare på Uppsala universitet lyser med sin frånvaro, men nyligen hörde jag talas om ett undantag. Jag vet inte vem det är och kommer inte ihåg varför han var bra, men ett undervisningsknep tänker jag någon gång låna från honom.
Innan
Turistens promenad
Rekommenderad från: 12 år
[kkratings]
En turist vill ta en promenad i Gamla Stan från busshållplatsen (punkt A) till sitt hotell (punkt B). Han vill ha en så lång rutt som möjligt. Han tycker att det är tråkigt att komma tillbaka
Kortlekar som ligger snyggt

Rekommenderad från: 15 år
[kkratings]
Tag en vanlig kortlek med 52 kort. Säg att kortleken ligger snyggt, ifall varje par av kort där ena ligger på den andra antingen har samma färg eller samma valör, samma sak gäller för det översta
Ska man plugga matte själv eller i grupp?
![]()
Studierna på universitetet skiljer sig mycket ifrån gymnasiestudier. Det kan verka först att det enda som förändrats är mängden arbete man måste utföra för att klara sig bra, men så enkelt är det inte.
Mängden "plugg" som måste ske är lika stor som
Ödlornas läsning

Rekommenderad från: 13 år
[kkratings]
Vi människor läser vanligtvis från vänster till höger och uppifrån och ner. Ödlor är inte lika snabba på att läsa, men de kan göra det på fler olika sätt. Ödlan kan läsa en bokstav och sedan
Spel på en remsa
Rekommenderad från: 15 år
[kkratings]
Det finns en rutig remsa 1xn:
Anders och Filip spelar ett spel. De turas om att göra drag: Anders får sätta ett kryss i en tom ruta och Filip får sätta en ring i en tom ruta. Dock får inte två
Tehuset

Rekommenderad från: 13 år
[kkratings]
55 indier och turkar träffades på ett tehus. Varje person drack antingen te eller kaffe. När en indier dricker te så talar hen alltid sanning och när hen dricker kaffe så luras hen alltid, medan
För svåra lektioner
![]()
Eleverna stirrar i tomma intet, läraren kan inte komma på tillräckliga förklaringar, alla lyssnar intensivt men ingen tar emot vad som sägs. Vad ska man göra när lektionen har blivit för svår? Och finns det någon poäng med att ha svåra
Ett matematiskt korttrick

Rekommenderad från: 12 år
[kkratings]
En trollkarl med förbundna ögon och hans assistent utför följande trick. Trollkarlen har 29 kort med talen 1 till 29 på. Han ger korten till någon person i publiken, som väljer ut två av dem.
Att täcka över en svart kvadrat

Rekommenderad från: 10 år
[kkratings]
På ett papper finns en bild på en svart kvadrat. Du har tillgång till 7 kvadratformade brickor av samma storlek som den ritade kvadraten. Hur ska du göra för att täcka över kvadraten med
Mattecirkel: lektion i logik
![]()
Första mötet med matematisk logik är för många påståendet "Jag ljuger". Det är förstås en paradox, eftersom någon som talar sanning, kan inte påstå att han ljuger. Och tvärtom, någon som ljuger, kan inte tala sanning om det. (Egentligen menas
Uppdelning i nästan lika heltal
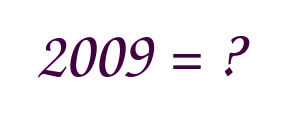
Rekommenderad från: 15 år
[kkratings]
På hur många sätt kan man skriva talet 2009 som en summa av några positiva nästan lika heltal? Talen kallas nästa lika om deras skillnad är (till beloppet) maximalt 1. Sätten betraktas som samma om
Hur man håller ett bra föredrag
![]()
Förra veckan befann jag mig på en mattekonferens i Glasgow. Temat var kategorifikationer, så ni kan gissa att de flesta av föredragen var ganska svåra. Det hände mer än sällan att jag bara förstod en liten del eller inte något alls.
Det lustiga är
Symmetrisk figur
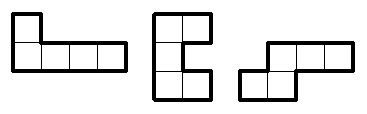
Rekommenderad från: 10 år
Förkunskaper: spegelsymmetri
[kkratings]
Bygg ihop bitarna nedan till en spegelsymmetrisk figur. Varje bit skall användas exakt en gång.
Visa lösningen
Det finns åtminstone tre
Klassiska bevis: Monges sats
Om du precis har börjat intressera dig för matematik, då säger jag grattis! Du kommer att bli fascinerad av problem, teorier och bevis många gånger!
Det är inte lika lätt om man fått matematiken serverad på ett guldfat sedan barnsben (eller
Mattecirkel: lektion i lådprincipen
![]()
Vår mattecirkel tuffar på vidare. Den är fortfarande med Anna, men eftersom jag tänkte skriva lite fiktion här, så skriver jag inte ut det i titeln.
För nyligen läste jag i en klok bok om hur man lär ut induktion. Bland annat fanns en påhittad
Tallskogen

Rekommenderad från: 12 år
[kkratings]
På ett område 1km x 1km växer en tallskog. Alla tallarna har diametern 50 cm. Visa att en fältbiolog kan hitta en ledig rektangel 10m x 20m i skogen, för att kunna sola där med alla sina vänner om
NMC 2009
![]()
Igår skedde en viktig etapp i att utse Sveriges vassaste (i matematik) gymnasieelever. Det var det nordiska matematiktvälingen NMC (Nordic Mathematical Contest). Ungefär 20 personer från varje land i Norden får delta i tävlingen, men det är inte så
Klassiska bevis: roten ur 2 irrationellt
![]()
Flera av mina bekanta har berättat för mig vad deras första möte med riktiga matematiska bevis var. Och man märker kanske inte först att det man läser eller hör om är så kallade riktiga bevis, förrän man läser ordet "bevis" explicit. De första
Ett hekto socker
Rekommenderad från: 12 år
[kkratings]
En balansvåg har två skålar. Om tyngderna på skålarna är lika visar balansvågen jämvikt. Annars visar den vilken skål som är tyngre.
Det finns en stor påse strösocker, en balansvåg samt en
Mattecirkel med Anna: lektion 2

Här är ett smakprov av vår andra lektion, som handlar om att väga saker på en balansvåg och avgöra om de är lätta, tunga, falska etc. Här nedan ser ni några av lektionens svåraste problem.
Nu kan man försöka analysera vad det är egentligen som
Kan man lära ut matte med hjälp av spel?
Eller en ekvivalent fråga: kan man lära sig matte med hjälp av spel?
Jag har lagt till en spelsida på bloggen med lite snodda småpussel. Syftet med detta är ännu oklart, men det fick mig att tänka på ovanstående frågor. Så nu menar jag alltså spel
Snigelns underbara resa

Rekommenderad från: 15 år
[kkratings]
En dag bestämde sig en snigel för att starta en resa. Snigeln rörde sig framåt längs med en rak sträcka i 6 minuter tills det var nog för dagen. Under den tiden kom några människor och tittade på
What the Best College Teachers Do
![]()
Även om man har ett riktigt jobb, ett rätt krävande sådant, så har man ibland lite tid att läsa böcker också. En dag såg jag en bok med titeln ovan liggande hemma hos min vän. "Jag vill vara en sådan!" tänkte jag, "hur gör man?" och bad om att få
Svenska eller engelska?
![]()
Imorgon skall jag hålla i en föreläsning om kategoriteori. Det är i en kurs som några doktorander går, och varje deltagare måste hålla i ett par föreläsningar själv. Vilket är jättebra, tycker jag, för man lär sig bäst genom att berätta materialet
Dela upp en lägenhet
Rekommenderad från: 12 år
[kkratings]
En lägenhet består av ett antal rum som kan ha olika areor. Det går att dela lägenheten mellan 2, 3 eller 4 hyresgäster så att varje person får bo på samma area (fast antalet rum kan vara olika).
Mattecirkel med Anna: lektion 1

Jag har precis börjat mattecirkeln med Anna, en elev som nu går i nian i Uppsala.
Det är många som frågat mig vad "mattecirkel" egentligen betyder, för det känns kanske lite dumt att kalla någonting för "cirkel" när bara två personer träffas. Men
Att bevisa
![]()
Idag startar min nya mattecirkel. Det är förvisso bara en elev i den än så länge, men jag kallar det hela mattecirkel i alla fall av en gammal vana. Mina mattecirklar brukar innehålla sådana problem som inte förekommer i vanliga skolan, utan snarare
Linjär avbildning
Jag ska försöka reda ut begreppet linjär avbildning. Det är trots allt det linjär algebra i stort sett handlar om.
För det första är linjär avbildning synonymt begrepp med linjär transformation, och båda varianterna används flitigt. Detta tyder på
Två fyrkanter
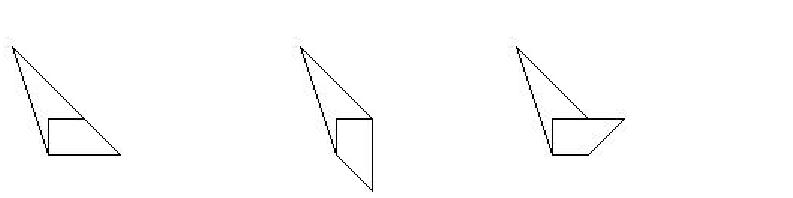
Rekommenderad från: 12 år
[kkratings]
Rita två fyrkanter, som tillsammans kan läggas ihop till
(i) En triangel, men också en femkant
(ii) Både en triangel, en fyrkant och en femkant.
Med "läggas ihop" menas att fyrkanterna inte
En liten inluppsrättningshistoria
![]()
I stort sett varje lärare spenderar många timmar av sitt liv på att rätta tentor och inlämningsuppgifter. Det kan vara frustrerande, om många personer gör olika fel. Det kan vara snabbt och lätträttat när alla gjort rätt. Men ofta är det tyvärr
Alternativa examinationsmetoder: munta
![]()
Det finns många olika sätt att genomföra sin undervisning. Läraren kan ha föreläsningar, lektioner, laborativa pass, case studies och diskussionstillfällen, bara för att nämna några. Men det många inte tänker på är att man också kan variera sig när
Bläckfiskarna

Rekommenderad från: 12 år
I havet bor många olika bläckfiskar. Om en bläckfisk har ett jämnt antal armar så talar den alltid sanning, men om den har udda anta armar så ljuger den alltid. En gång sade den gröna bläckfisken till den
Inlärning
![]()
För länge sedan läste jag att man lär sig bäst när det nya i materialet utgör 30% . Med andra ord, 70% av det man läser, hör och ser ska helst redan vara bekant. Det tycker jag är en ganska rimlig siffra, dock går inte det ihop med begreppet
Kvartscirkel
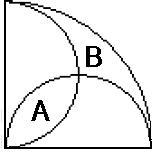
Rekommenderad från: 15 år
Från början har vi en kvartscirkel med radie 1 cm. Gränserna för kvartscirkeln utgör diametrar för två mindre cirklar, deras halvor syns på bilden.
i) Hur förhåller sig areorna A och B?
ii) Vad
Att sätta händerna i degen
![]()
I den stora boken "Algebra" av Grillet liknar författaren viss matematikinlärning med att knåda deg. Att lära sig vissa saker går bara om man själv försöker härleda eller använda dem. Till exempel matrisräkning kan man inte utantill om man inte
Kvadratuppdelning
Rekommenderad från: 12 år
Visa att en kvadrat kan delas upp i n stycken mindre kvadrater för alla n>5. Med "att dela upp" menas att vi klipper en kvadrat så att alla erhållna delar också är kvadrater och det blir inga bitar över.
Hjärtfigur
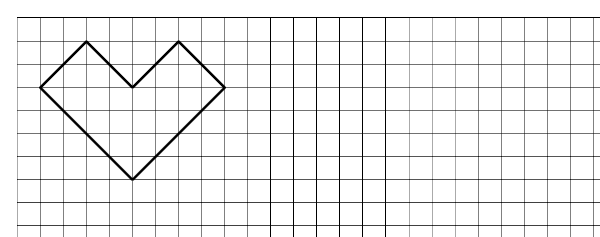
Rekommenderad från: 10 år
Dela upp hjärtfiguren nedan i 8 likadana delar. Delarna räknas som likadana om de har samma form och storlek (de kan dock vara placerade på olika sätt).
Visa lösningen
Första lösningen kommer från min
Induktion (matematisk sådan)

Från Wikipedia: Låt P(n) vara ett påstående som har att göra med ett positivt heltal n, och antag att följande påståenden är sanna:
P(1) är sant.
.
Då är påståendet P(n) sant för varje val av det positiva heltalet n.
Lätt som en plätt,
Att använda olika färger
![]()
Jag har precis haft föreläsningar med en ny lektor, och hans tavelteknik var fascinerande! Förutom att han talade tydligt och klart, förklarade långsamt och bra, tittade mot klassen och aldrig drog över tiden, så var han en mästare på att använda
Blåröda tallinjen

Rekommenderad från: 15 år
Förkunskaper: intervall, tallinjen, delbarhet, potenser.
På reella tallinjen markerade Johan alla kvadrater på positiva heltal. Varje erhållet intervall delade han sedan i två lika stora delar, de vänstra
Finns det dumma frågor?
![]()
Man hör jämt vissa lärare säga "det finns inga dumma frågor". Man hör också ofta sina kursare eller klasskompisar klaga på någon störig typ, som "alltid ställer korkade frågor". Så vilket är det som gäller?
Själva frågan som ställs är svår att
Parkering
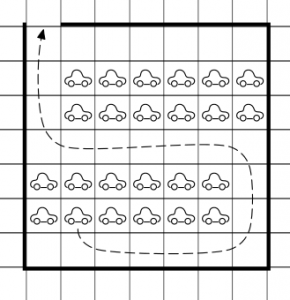
Rekommenderad från: 10 år
[kkratings]
I staden Bilköping finns en parkering med plats för 7x7 bilar. Man kan komma in endast genom porten, resten av parkeringsplatsen är omsluten med staket. En vakt vill parkera så många bilar som
Första lektionen

Lektionerna nummer ett är nu avklarade!
Det är alltid lite mer nervöst att ha lektion i en ny kurs för första gången, än med en ny grupp, men nu hände båda sakerna på en gång. Sedan var det en ny grupp tre gången till :). Varje gång gick jag
Mattecirkel i Uppsala
![]()
Högstadiets matematiktävling 08/09 har precis avslutats och jag gratulerar vinnaren, Lien Tran från Rödabergsskolan i Stockholm! Här kan ni se på problemen för övrigt. Några elever från min kära residens Uppsala deltog också, de går förmodligen i
Vektorrum
![]()
Vad är det? Ett rum där vektorerna bor, såklart! Vill man veta vad som försigår där, så kan man lyssna på låten Tänk om jag vore en skalärprodukt.
Men om man ska vara matematiskt petig, så är vektorrum en mängd med vektorer, där diverse räknelagar
W2B, IT2A, IT2B, KandMa1
![]()
Hittils har lätt förvirring rått angående mina grupper. Nu har jag till slut förstått att W2B (miljö- och vattenteknik-programmet, årskurs 2, grupp B) och KandMa1 (kandidatprogrammet i matematik) har en gemensam föreläsare (min handledare Walter
Linjär algebra
![]()
Nästa vecka börjar jag undervisa på kursen “Linjär algebra II” för fyra olika studentgrupper. Det är alltså stor risk för förvirring, man vill å ena sidan inte missa att säga något viktigt till någon grupp och å andra sidan vill man variera sina
 Ny mellanstadietävling
I Sverige finns en tradion av tävlingar för högstadier (HMT, Pythagoras Quest, Sigma8) och gymnasiet (SMT) men nästa inga tävlingar finns för mellanstadiet!
Vissa skolor anordnar förstås Känguru, men det är en individuell
Ny mellanstadietävling
I Sverige finns en tradion av tävlingar för högstadier (HMT, Pythagoras Quest, Sigma8) och gymnasiet (SMT) men nästa inga tävlingar finns för mellanstadiet!
Vissa skolor anordnar förstås Känguru, men det är en individuell I veckan besökte jag Matematikbiennalen i Karlstad, en stor händelse för mattelärare, där ett par tusen besökare fick vara med om föreläsningar, workshops och utställningar. Allt handlade om matematikundervisning.
Jag höll i en föreläsning där
I veckan besökte jag Matematikbiennalen i Karlstad, en stor händelse för mattelärare, där ett par tusen besökare fick vara med om föreläsningar, workshops och utställningar. Allt handlade om matematikundervisning.
Jag höll i en föreläsning där I januari anordnades en fantastiskt konferens i Piteå med kodnamnet Knuth80. Den berömda matematikern, programmeraren och författaren Donald E. Knuth (skaparen av TeX) fyllde 80 år och hans vänner och familj bestämde sig såklart att anordna en
I januari anordnades en fantastiskt konferens i Piteå med kodnamnet Knuth80. Den berömda matematikern, programmeraren och författaren Donald E. Knuth (skaparen av TeX) fyllde 80 år och hans vänner och familj bestämde sig såklart att anordna en Korstal 2015
Fyll i precis som ett vanligt korsord (men endast med siffror). Obs! Inga tal börjar med noll.
Vågrätt:
1. En tvåpotens (det vill säga 2n).
7. Har samma siffersumma som vågrätt 15.
8. Talet siffersumma är
Korstal 2015
Fyll i precis som ett vanligt korsord (men endast med siffror). Obs! Inga tal börjar med noll.
Vågrätt:
1. En tvåpotens (det vill säga 2n).
7. Har samma siffersumma som vågrätt 15.
8. Talet siffersumma är Kvadrater i trappan
Vilket är det minsta antalet kvadrater som man kan klippa upp trappan nedan i? Man får bara klippa längs med rutnätets linjer. (Det är alltså 15 trappsteg i trappan.)
Visa lösningen
Det finns 15 små
Kvadrater i trappan
Vilket är det minsta antalet kvadrater som man kan klippa upp trappan nedan i? Man får bara klippa längs med rutnätets linjer. (Det är alltså 15 trappsteg i trappan.)
Visa lösningen
Det finns 15 små  Kubkonstruktion
En konstruktion som är byggd av likadana kuber ser ut på samma sätt både framifrån och högerifrån. Vilket är det minsta antal kuber som konstruktionen kan bestå av? (Konstruktionen följer fysikens
Kubkonstruktion
En konstruktion som är byggd av likadana kuber ser ut på samma sätt både framifrån och högerifrån. Vilket är det minsta antal kuber som konstruktionen kan bestå av? (Konstruktionen följer fysikens Öriken
Det Stora och det Lilla Riket är båda rektangulära öar och uppdelade i rektangulära landskap. I varje landskap finns en väg som går längs med en av diagonalerna. På varje ö bildar vägarna en sluten rutt, som inte går igenom
Öriken
Det Stora och det Lilla Riket är båda rektangulära öar och uppdelade i rektangulära landskap. I varje landskap finns en väg som går längs med en av diagonalerna. På varje ö bildar vägarna en sluten rutt, som inte går igenom Fyrhörningens diagonal
I fyrhörningen ABCD är AB = 5 cm, BC = 17 cm, CD = 5 cm, DA = 9 cm och sträckan BD är ett helt antal cm. Hur lång är sträckan
Fyrhörningens diagonal
I fyrhörningen ABCD är AB = 5 cm, BC = 17 cm, CD = 5 cm, DA = 9 cm och sträckan BD är ett helt antal cm. Hur lång är sträckan Första, andra och tredje avsnittet av Genikampen innehöll en hel del matte, medan avsnitt fyra och fem var mycker mer fysikinriktade. Jag har inte så bra förståelse för fysik, så jag ska försöka framlägga hur jag försökte göra mitt bästa genom att
Första, andra och tredje avsnittet av Genikampen innehöll en hel del matte, medan avsnitt fyra och fem var mycker mer fysikinriktade. Jag har inte så bra förståelse för fysik, så jag ska försöka framlägga hur jag försökte göra mitt bästa genom att Tack till David Nilsson som påminnt mig om en gammal klassiker!
Rekommenderad från: 13 år
En apa är i ett 100-våningshus och vill veta vilken den högsta våningen är som den kan släppa en kokosnöt ifrån utan att den går sönder när det träffar
Tack till David Nilsson som påminnt mig om en gammal klassiker!
Rekommenderad från: 13 år
En apa är i ett 100-våningshus och vill veta vilken den högsta våningen är som den kan släppa en kokosnöt ifrån utan att den går sönder när det träffar Tredje avsnittet av Genikampen innehöll mycket matte! Så mycket att det inte hanns med att skriva om det innan avsnitt fyra kom ut. Avsnitt fyra och fem kommer jag däremot att slå ihop till ett inlägg.
Avsnitt tre innehöll tre tävlingar:
Tredje avsnittet av Genikampen innehöll mycket matte! Så mycket att det inte hanns med att skriva om det innan avsnitt fyra kom ut. Avsnitt fyra och fem kommer jag däremot att slå ihop till ett inlägg.
Avsnitt tre innehöll tre tävlingar: Det tredje avsnittet av Genikampen var sprängfyllt med matte! Det var så pass mycket matte att jag behöver dela upp inlägget om det i två delar. I första delen vill jag presentera problemen som ingick i den andra lagtävlingen, samt lösningar till de
Det tredje avsnittet av Genikampen var sprängfyllt med matte! Det var så pass mycket matte att jag behöver dela upp inlägget om det i två delar. I första delen vill jag presentera problemen som ingick i den andra lagtävlingen, samt lösningar till de  Andra avsnittet innehöll kanske inte lika mycket matte som första avsnittet, men det betyder ju inte att man inte skulle vara smart för att klara tävlingarna. Och allt som har med kreativt tänkande att göra kan jag om jag vill koppla ihop med matte
Andra avsnittet innehöll kanske inte lika mycket matte som första avsnittet, men det betyder ju inte att man inte skulle vara smart för att klara tävlingarna. Och allt som har med kreativt tänkande att göra kan jag om jag vill koppla ihop med matte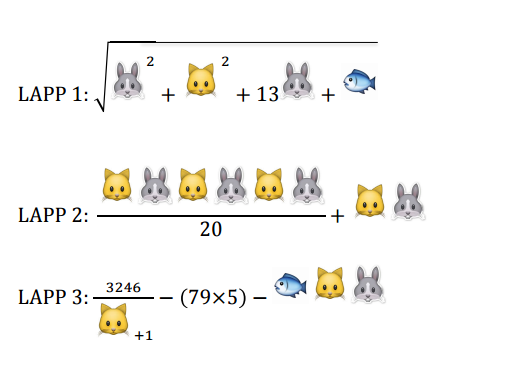 I höst är jag en av deltagarna i SVT:s program Genikampen. Programmet går i åtta avsnitt och jag tänkte beskriva händelserna i avsnitten ur ett matematiskt perspektiv.
Själv är jag matteintresserad och har övat mycket i problemlösning. Jag tror
I höst är jag en av deltagarna i SVT:s program Genikampen. Programmet går i åtta avsnitt och jag tänkte beskriva händelserna i avsnitten ur ett matematiskt perspektiv.
Själv är jag matteintresserad och har övat mycket i problemlösning. Jag tror Det här roliga problemet har jag fått av min kompis Fredrik från Genikampen-2015!
Rekommenderad från: 15 år
Tre kvadrater är ritade bredvid varandra. Tre linjer dras från ett hörn som bilden visar. Bestäm summan av de tre utsatta vinklarna (i
Det här roliga problemet har jag fått av min kompis Fredrik från Genikampen-2015!
Rekommenderad från: 15 år
Tre kvadrater är ritade bredvid varandra. Tre linjer dras från ett hörn som bilden visar. Bestäm summan av de tre utsatta vinklarna (i Rekommenderad från: 15 år
Du sitter i en fängelsehåla och en vakt kommer till dig med ett erbjudande. Han säger att han kommer lägga upp mynt (totalt 64 st.) på ett schackbräde, ett mynt i varje ruta och det kommer vara slumpat för varje mynt
Rekommenderad från: 15 år
Du sitter i en fängelsehåla och en vakt kommer till dig med ett erbjudande. Han säger att han kommer lägga upp mynt (totalt 64 st.) på ett schackbräde, ett mynt i varje ruta och det kommer vara slumpat för varje mynt Rekommenderad från: 12 år
En hemlig byggnad består av många rum som ser exakt likadana ut och som är kopplade i en stor ring med små korridorer. I varje rum finns en lampa och en lampknapp. En spion hamnade i ett av rummen. Hur ska han bestämma
Rekommenderad från: 12 år
En hemlig byggnad består av många rum som ser exakt likadana ut och som är kopplade i en stor ring med små korridorer. I varje rum finns en lampa och en lampknapp. En spion hamnade i ett av rummen. Hur ska han bestämma Det är riktigt kul att höra att så många är positiva till idén att ha Mattekollo nu i sommar! Här tänkte jag skriva lite mer detaljerat om vad jag har för vision.
Var ska det vara?
Då jag själv åkt på kollo som barn vet jag att jag inte bara
Det är riktigt kul att höra att så många är positiva till idén att ha Mattekollo nu i sommar! Här tänkte jag skriva lite mer detaljerat om vad jag har för vision.
Var ska det vara?
Då jag själv åkt på kollo som barn vet jag att jag inte bara  Nästan varje vecka får jag träffa elever som blir glada av mina lektioner. Många av dem går på Matteklubben i Uppsala - kommunens satsning på begåvade elever i matematik. Senast igår fick jag en kommentar om att det "lyser om barnen" som går från
Nästan varje vecka får jag träffa elever som blir glada av mina lektioner. Många av dem går på Matteklubben i Uppsala - kommunens satsning på begåvade elever i matematik. Senast igår fick jag en kommentar om att det "lyser om barnen" som går från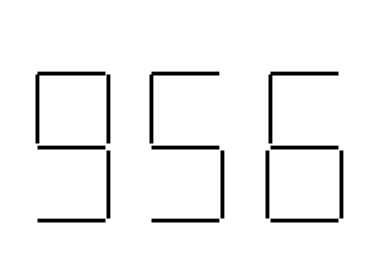 Det finns många tändsticksproblem som går ut på att flytta tändstickor för att få kvar någon särskild figur eller för att en viss likhet ska uppfyllas. Ett exempel på ett sådant problem kan du hitta i tidningen Forskning och Framsteg.
Här är dock
Det finns många tändsticksproblem som går ut på att flytta tändstickor för att få kvar någon särskild figur eller för att en viss likhet ska uppfyllas. Ett exempel på ett sådant problem kan du hitta i tidningen Forskning och Framsteg.
Här är dock Finalresultat
För en dryg vecka sedan hölls finalen i Högstadiets Matematiktävling i Stockholm! 49 skarpa hjärnor var med och löste 6 matematiska problem på tid och en kom ut som vinnare. Grattis Björn Magnusson från Lund som fick fullpoäng på alla
Finalresultat
För en dryg vecka sedan hölls finalen i Högstadiets Matematiktävling i Stockholm! 49 skarpa hjärnor var med och löste 6 matematiska problem på tid och en kom ut som vinnare. Grattis Björn Magnusson från Lund som fick fullpoäng på alla  Minsta eleverna som går i Matteklubben är de i åk 2-4. Du kan läsa om första, andra och tredje träffen med gruppen.
Nytt sätt att sitta
Den sista gången för terminen testade vi en ny bordsuppställning. Vanligtvis brukar vi behålla lektionssalen
Minsta eleverna som går i Matteklubben är de i åk 2-4. Du kan läsa om första, andra och tredje träffen med gruppen.
Nytt sätt att sitta
Den sista gången för terminen testade vi en ny bordsuppställning. Vanligtvis brukar vi behålla lektionssalen Matteklubben är Uppsala kommuns satsning på begåvade elever i matematik. Jag har äran att förbereda aktiviteterna som vi håller på med och vara en av lärarna. Du kan kolla upp var vi gjorde på första träffen, andra träffen och tredje träffen innan
Matteklubben är Uppsala kommuns satsning på begåvade elever i matematik. Jag har äran att förbereda aktiviteterna som vi håller på med och vara en av lärarna. Du kan kolla upp var vi gjorde på första träffen, andra träffen och tredje träffen innan Korstal 2014
Fyll i precis som ett vanligt korsord (men endast med siffror). Obs! Inga tal börjar med noll.
Ladda ner för utskrift
Vågrätt:
1. Delbart med 9
4. Valören på en svensk sedel
5. Alla siffror i talet är
Korstal 2014
Fyll i precis som ett vanligt korsord (men endast med siffror). Obs! Inga tal börjar med noll.
Ladda ner för utskrift
Vågrätt:
1. Delbart med 9
4. Valören på en svensk sedel
5. Alla siffror i talet är Månskäran
I hur många delar kan man som mest dela upp månskäran med hjälp av 5 raka linjer? Delarna får inte arrangeras om mellan skärningarna.
Visa lösningen
Månskäran kan delas upp i 21 delar till exempel så som
Månskäran
I hur många delar kan man som mest dela upp månskäran med hjälp av 5 raka linjer? Delarna får inte arrangeras om mellan skärningarna.
Visa lösningen
Månskäran kan delas upp i 21 delar till exempel så som Shejkens slott
En shejk har ett slott som ser ut som en 6x6-kvadrat indelad i 1x1-rum. I mitten av varje vägg finns en dörr mellan rummen. Shejken ger order till hovbyggaren att ta bort några väggar, så att det bara bildas rum av
Shejkens slott
En shejk har ett slott som ser ut som en 6x6-kvadrat indelad i 1x1-rum. I mitten av varje vägg finns en dörr mellan rummen. Shejken ger order till hovbyggaren att ta bort några väggar, så att det bara bildas rum av Synliga rutor
På ett rutat papper har man markerat 9 blå rutor så som bilden nedan visar. Från punkten A kan man (helt eller delvis) se 5 av de blå rutorna. Hur många av rutorna kan man som mest se om man får välja en annan punkt
Synliga rutor
På ett rutat papper har man markerat 9 blå rutor så som bilden nedan visar. Från punkten A kan man (helt eller delvis) se 5 av de blå rutorna. Hur många av rutorna kan man som mest se om man får välja en annan punkt Termometrar
Två kvicksilvertermometrar hänger bredvid varandra så som bilden visar. Vid vilken temperatur kommer kvicksilvret vara på samma höjd i båda termometrarna?
Visa lösningen
60 steg (70-10) på den första
Termometrar
Två kvicksilvertermometrar hänger bredvid varandra så som bilden visar. Vid vilken temperatur kommer kvicksilvret vara på samma höjd i båda termometrarna?
Visa lösningen
60 steg (70-10) på den första Kvadrat i kvadrat i kvadrat
I en kvadrat med sidan 1 m placerade man en annan kvadrat, vars hörn hamnade precis på mittpunkterna av den första kvadratens sidor. Likadant placerade man den tredje kvadraten inuti den andra. Vilken
Kvadrat i kvadrat i kvadrat
I en kvadrat med sidan 1 m placerade man en annan kvadrat, vars hörn hamnade precis på mittpunkterna av den första kvadratens sidor. Likadant placerade man den tredje kvadraten inuti den andra. Vilken Minsta eleverna som går i Matteklubben är de i åk 2-4. Du kan också läsa om den första träffen och den andra träffen med gruppen.
Från början hade vi tänkt att både ha med en del med blandade problem och en tematisk del. Vi hann dock bara gå
Minsta eleverna som går i Matteklubben är de i åk 2-4. Du kan också läsa om den första träffen och den andra träffen med gruppen.
Från början hade vi tänkt att både ha med en del med blandade problem och en tematisk del. Vi hann dock bara gå Här i kommentarerna kan du diskutera hemuppgiften. Skriv om du har frågor eller förslag på lösning/svar.
• I ett höghus med 100 våningar finns en hiss, som bara har två knappar: ”+7” och ”-9”. Den första knappen får hissen att gå upp sju
Här i kommentarerna kan du diskutera hemuppgiften. Skriv om du har frågor eller förslag på lösning/svar.
• I ett höghus med 100 våningar finns en hiss, som bara har två knappar: ”+7” och ”-9”. Den första knappen får hissen att gå upp sju Matteklubben är Uppsala kommuns satsning på begåvade elever i matematik. Jag har äran att förbereda aktiviteterna som vi håller på med och vara en av lärarna. Du kan kolla upp var vi gjorde på första träffen och andra träffen innan du läser
Matteklubben är Uppsala kommuns satsning på begåvade elever i matematik. Jag har äran att förbereda aktiviteterna som vi håller på med och vara en av lärarna. Du kan kolla upp var vi gjorde på första träffen och andra träffen innan du läser På lektionen bevisade vi att vinkelsumman i en godtycklig triangel är 180° och en i fyrhörning 360°. Hur blir det med en femhörning, sexhörning osv.? Och hur bevisar man resultatet?
Det är inte bara månghörningar som har en viss bestämd
På lektionen bevisade vi att vinkelsumman i en godtycklig triangel är 180° och en i fyrhörning 360°. Hur blir det med en femhörning, sexhörning osv.? Och hur bevisar man resultatet?
Det är inte bara månghörningar som har en viss bestämd Under andra matteträffen med högstadiet hade vi 19 elever som besökte oss. Vi var 3 lärare plus en till som hjälpte lite grann. Det var alldeles lagom för en grupp med elever som inte så ofta räcker upp handen. Men hade eleverna varit lika aktiva
Under andra matteträffen med högstadiet hade vi 19 elever som besökte oss. Vi var 3 lärare plus en till som hjälpte lite grann. Det var alldeles lagom för en grupp med elever som inte så ofta räcker upp handen. Men hade eleverna varit lika aktiva Minsta eleverna som går i Matteklubben är de i åk 2-4. Du kan också läsa om den första träffen med gruppen här på bloggen.
På den andra träffen kom färre elever, men de var precis lagom många för att vi skulle hinna prata med alla. Barn i
Minsta eleverna som går i Matteklubben är de i åk 2-4. Du kan också läsa om den första träffen med gruppen här på bloggen.
På den andra träffen kom färre elever, men de var precis lagom många för att vi skulle hinna prata med alla. Barn i Här i kommentarerna kan du diskutera hemuppgiften. Skriv om du har frågor eller förslag på lösning/svar.
• En viss figur hade arean 12 cm2. Om den figuren förminskas så att alla dess sidor bli hälften så stora, vad kommer dess area att bli
Här i kommentarerna kan du diskutera hemuppgiften. Skriv om du har frågor eller förslag på lösning/svar.
• En viss figur hade arean 12 cm2. Om den figuren förminskas så att alla dess sidor bli hälften så stora, vad kommer dess area att bli Matteklubben är Uppsala kommuns satsning på begåvade elever i matematik. Jag har äran att förbereda aktiviteterna som vi håller på med och vara en av lärarna. Du kan kolla upp var vi gjorde på första träffen innan du läser vidare.
36 elever och 6
Matteklubben är Uppsala kommuns satsning på begåvade elever i matematik. Jag har äran att förbereda aktiviteterna som vi håller på med och vara en av lärarna. Du kan kolla upp var vi gjorde på första träffen innan du läser vidare.
36 elever och 6 Rekommenderad från: 13 år
[kkratings]
Visa att man kan stryka några siffror i början och några i slutet av talet
(talet består av 2000 siffror), så att summan av de resterande siffrorna blir delbart med 2014.
Visa lösningen
Om
Rekommenderad från: 13 år
[kkratings]
Visa att man kan stryka några siffror i början och några i slutet av talet
(talet består av 2000 siffror), så att summan av de resterande siffrorna blir delbart med 2014.
Visa lösningen
Om Detta är de inofficiella (dagen-efter) lösningar till SMT-kvalet som hölls den 30:e september på gymnasieskolorna över hela Sverige. De officiella lösningarna kommer att komma upp på SMT:s hemsida.
Problem 1
Ett tåg kör fram och tillbaka
Detta är de inofficiella (dagen-efter) lösningar till SMT-kvalet som hölls den 30:e september på gymnasieskolorna över hela Sverige. De officiella lösningarna kommer att komma upp på SMT:s hemsida.
Problem 1
Ett tåg kör fram och tillbaka Matteklubben har haft lektioner för grupperna åk 2-4, åk 5-6 och sist ut var högstadieeleverna, åk 7-9.
Denna gång kom en hanterbar mängd elever, 25 stycken. Det är ganska lagom för den åldern, nackdelen med för många elever är att någon som är
Matteklubben har haft lektioner för grupperna åk 2-4, åk 5-6 och sist ut var högstadieeleverna, åk 7-9.
Denna gång kom en hanterbar mängd elever, 25 stycken. Det är ganska lagom för den åldern, nackdelen med för många elever är att någon som är Minsta eleverna som går i Matteklubben är de i åk 2-4. Du kan också läsa om första lektionen i åk 5-6.
Även om eleverna var små, fyllde de salen så att det nästan blev lite trångt! Totalt var de 40 stycken och denna gång var vi 5 lärare (vi
Minsta eleverna som går i Matteklubben är de i åk 2-4. Du kan också läsa om första lektionen i åk 5-6.
Även om eleverna var små, fyllde de salen så att det nästan blev lite trångt! Totalt var de 40 stycken och denna gång var vi 5 lärare (vi Här i kommentarerna kan du diskutera hemuppgiften. Skriv om du har frågor eller förslag på lösning/svar.
• Hur många olika armband kan man tillverka av 3 svarta och 2 vita pärlor? På bilden har du ett exempel.
• Hur många svart-vita
Här i kommentarerna kan du diskutera hemuppgiften. Skriv om du har frågor eller förslag på lösning/svar.
• Hur många olika armband kan man tillverka av 3 svarta och 2 vita pärlor? På bilden har du ett exempel.
• Hur många svart-vita Matteklubben är Uppsala kommuns satsning på begåvade elever i matematik. Jag har äran att förbereda aktiviteterna som vi håller på med och vara en av lärarna. Här på bloggen tänkte jag lägga ut materialet som vi tar upp på träffarna, samt skriva
Matteklubben är Uppsala kommuns satsning på begåvade elever i matematik. Jag har äran att förbereda aktiviteterna som vi håller på med och vara en av lärarna. Här på bloggen tänkte jag lägga ut materialet som vi tar upp på träffarna, samt skriva Fler och fler människor lär sig att programmera, vilket är bra, för fler och fler bra programmerare behövs. Än så länge finns ingen obligatorisk programmering i grundskolan i Sverige, men vem vet, det kanske är på gång?
Jag har undervisat inte
Fler och fler människor lär sig att programmera, vilket är bra, för fler och fler bra programmerare behövs. Än så länge finns ingen obligatorisk programmering i grundskolan i Sverige, men vem vet, det kanske är på gång?
Jag har undervisat inte En avhandling startade det hela. Det handlade om situationen för barnen, som har det lätt i skolan. I matematik! Ja, just det, lätt i matematik, inte dem vi brukar betrakta som barn med problem i skolan (och inte heller dem man brukar forska på).
En avhandling startade det hela. Det handlade om situationen för barnen, som har det lätt i skolan. I matematik! Ja, just det, lätt i matematik, inte dem vi brukar betrakta som barn med problem i skolan (och inte heller dem man brukar forska på). När någon ställer frågan "Vad är matematik för dig?" svarar jag ibland "Att tänka." Det kan tolkas som ett luddigt svar eller att jag kanske tror att matematik är viktigare än allt annat. Men så är inte riktigt fallet och jag ska försöka visa vad
När någon ställer frågan "Vad är matematik för dig?" svarar jag ibland "Att tänka." Det kan tolkas som ett luddigt svar eller att jag kanske tror att matematik är viktigare än allt annat. Men så är inte riktigt fallet och jag ska försöka visa vad Rekommenderad från: 12 år
[kkratings]
Man gjorde tre snitt och delade upp ett träblock i åtta mindre rätblock. På bilden anges ytarean för de sju synliga bitarna. Hur stor är ytan på den biten som inte syns?
Visa
Rekommenderad från: 12 år
[kkratings]
Man gjorde tre snitt och delade upp ett träblock i åtta mindre rätblock. På bilden anges ytarean för de sju synliga bitarna. Hur stor är ytan på den biten som inte syns?
Visa Om du inte redan har sett 2048-pusslet, som blivit stort online, så kan du testa att spela det på http://gabrielecirulli.github.io/2048 Det går ut på att kombinera ihop tvåpotenser (från början 2:or och 4:or) så att det bildas 2048.
Varning:
Om du inte redan har sett 2048-pusslet, som blivit stort online, så kan du testa att spela det på http://gabrielecirulli.github.io/2048 Det går ut på att kombinera ihop tvåpotenser (från början 2:or och 4:or) så att det bildas 2048.
Varning:  Grattis på Pi-dagen!
Talet pi är förstås relaterat till cirklarnas area och radie, men följande uppgift kan du lösa utan att kunna några formler.
Vilken kvadrat har störst orange area?
(Även om du kan använda dig av formler, prova att
Grattis på Pi-dagen!
Talet pi är förstås relaterat till cirklarnas area och radie, men följande uppgift kan du lösa utan att kunna några formler.
Vilken kvadrat har störst orange area?
(Även om du kan använda dig av formler, prova att Den 1 mars hölls Uppsalas första Matteregatta för högstadiet! Två skolor deltog: Gluntens Montessoriskola samt Uppsala Musikklasser, både respresenterade med ett lag. Stort tack till Katedralskolans mattecirkel som hjälpte till att organisera
Den 1 mars hölls Uppsalas första Matteregatta för högstadiet! Två skolor deltog: Gluntens Montessoriskola samt Uppsala Musikklasser, både respresenterade med ett lag. Stort tack till Katedralskolans mattecirkel som hjälpte till att organisera Skämtet är till för en bred grupp läsare som har läst homologisk algebra:
Förklaring
Skämtets skapare: Sebastian Öberg
Sitter du som läsare på några bra/dåliga matteskämt? Skriv gärna i
Skämtet är till för en bred grupp läsare som har läst homologisk algebra:
Förklaring
Skämtets skapare: Sebastian Öberg
Sitter du som läsare på några bra/dåliga matteskämt? Skriv gärna i Mattebloggens decembertävling är nu avslutad. Tack alla som deltog!
Vinnare
Tävlingens vinnare är en person med kodnamnet $ som fick mest poäng av alla och alltså vunnit ett exemplar av boken Matematisk utflykt. Grattis $!
Alla andra
Mattebloggens decembertävling är nu avslutad. Tack alla som deltog!
Vinnare
Tävlingens vinnare är en person med kodnamnet $ som fick mest poäng av alla och alltså vunnit ett exemplar av boken Matematisk utflykt. Grattis $!
Alla andra Korstal 2013
[kkratings]
Fyll i precis som ett vanligt korsord (men endast med siffror). Obs! Inga tal börjar med noll.
Lös gärna korstalet tillsammans med familj eller vänner! Ladda ner för
Korstal 2013
[kkratings]
Fyll i precis som ett vanligt korsord (men endast med siffror). Obs! Inga tal börjar med noll.
Lös gärna korstalet tillsammans med familj eller vänner! Ladda ner för Ett land utan korsningar
[kkratings]
I ett sagoland finns 8 städer. Från varje stad leder 4 vägar och inga vägar korsar varandra. Rita kartan över landet genom att beteckna städerna med punkter och vägarna med
Ett land utan korsningar
[kkratings]
I ett sagoland finns 8 städer. Från varje stad leder 4 vägar och inga vägar korsar varandra. Rita kartan över landet genom att beteckna städerna med punkter och vägarna med Fram och tillbaka igen
[kkratings]
Från by A till by B leder en enda väg som är 15 km lång. Klockan 9:30 började en hob promenera med hastigheten 4 km/h från A till B. Nästa dag startade han klockan 11:00 från byn B och
Fram och tillbaka igen
[kkratings]
Från by A till by B leder en enda väg som är 15 km lång. Klockan 9:30 började en hob promenera med hastigheten 4 km/h från A till B. Nästa dag startade han klockan 11:00 från byn B och För circa en månad sedan hölls kvalomgången i Högstadiets Matematiktävling. Det är en tävling i problemlösning som riktar sig till årskurs 6-9, men självfallet lyckas eleverna i årskurs 8-9 få bäst resultat. Därför är det mest elever från dessa
För circa en månad sedan hölls kvalomgången i Högstadiets Matematiktävling. Det är en tävling i problemlösning som riktar sig till årskurs 6-9, men självfallet lyckas eleverna i årskurs 8-9 få bäst resultat. Därför är det mest elever från dessa Tjocka och tunna hårband
[kkratings]
På bordet ligger sex hårband som inte nuddar varandra. Ovanpå dem ligger ett papper som delvis täcker dem (se bild). Man vet att tre av hårbanden är tunna, medan tre är tjocka och att
Tjocka och tunna hårband
[kkratings]
På bordet ligger sex hårband som inte nuddar varandra. Ovanpå dem ligger ett papper som delvis täcker dem (se bild). Man vet att tre av hårbanden är tunna, medan tre är tjocka och att Feta streck
[kkratings]
Triangeln på bilden är uppdelad i fyra trianglar och tre fyrhörningar med de feta strecken.
Fyrhörningarnas omkretser tillsammans är 25 cm. Summan av omkretsarna för de fyra trianglarna är 20 cm.
Feta streck
[kkratings]
Triangeln på bilden är uppdelad i fyra trianglar och tre fyrhörningar med de feta strecken.
Fyrhörningarnas omkretser tillsammans är 25 cm. Summan av omkretsarna för de fyra trianglarna är 20 cm. Figur i fyra delar
[kkratings]
Dela upp figuren på bilden i fyra likadana delar.
Visa lösningen
På följande sätt kan man dela upp figuren:
Figur i fyra delar
[kkratings]
Dela upp figuren på bilden i fyra likadana delar.
Visa lösningen
På följande sätt kan man dela upp figuren:
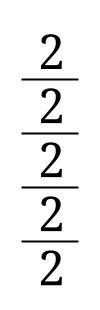 Två delat med två
[kkratings]
Bråkuppställningen på bilden är lite konstig, eftersom det inte går att tyda vad som ska delas med vad i vilken ordning. Du får göra bråkstrecken olika långa för att kunna räkna ut
Två delat med två
[kkratings]
Bråkuppställningen på bilden är lite konstig, eftersom det inte går att tyda vad som ska delas med vad i vilken ordning. Du får göra bråkstrecken olika långa för att kunna räkna ut Har du läst om hur man hittar pythagoreiska tripplar i cirklar? I artikelserien träffar vi på många cirklar som har några punkter med heltalskoordinater på periferin.
Men oftast är antalet punkter delbart med 4 (cirkeln är centralsymmetrisk i
Har du läst om hur man hittar pythagoreiska tripplar i cirklar? I artikelserien träffar vi på många cirklar som har några punkter med heltalskoordinater på periferin.
Men oftast är antalet punkter delbart med 4 (cirkeln är centralsymmetrisk i Rekommenderad från: 13 år
[kkratings]
Du har tre påsar med hundra mynt i varje. I en av påsarna väger alla mynten 9,9g, i en annan väger alla 10g och en tredje väger alla 10,1g, men du vet inte vilka mynt som ligger i vilken påse. Du har
Rekommenderad från: 13 år
[kkratings]
Du har tre påsar med hundra mynt i varje. I en av påsarna väger alla mynten 9,9g, i en annan väger alla 10g och en tredje väger alla 10,1g, men du vet inte vilka mynt som ligger i vilken påse. Du har 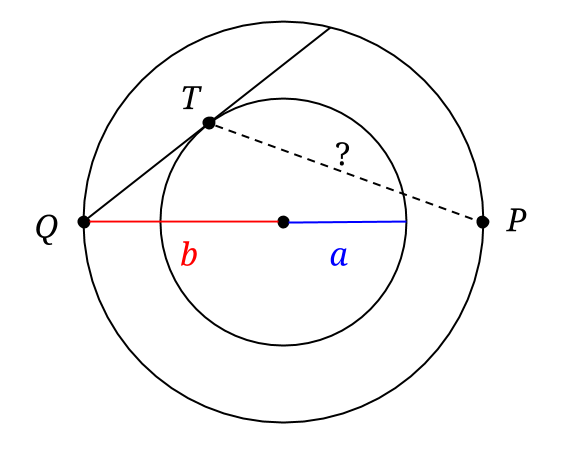 Nyligen hölls SM i matte för gymnasister, som kallas Skolornas Matematiktävling. Tävlingen bestod av 6 uppgifter som eleverna fick lösa under 5 timmar.
De officiella lösningarna har inte kommit upp än, så jag tänkte föreslå egna. Samt kommentera på
Nyligen hölls SM i matte för gymnasister, som kallas Skolornas Matematiktävling. Tävlingen bestod av 6 uppgifter som eleverna fick lösa under 5 timmar.
De officiella lösningarna har inte kommit upp än, så jag tänkte föreslå egna. Samt kommentera på  I föregående del avslöjade vi processen med vilken vi kan förstora koordinatsystem på så sätt att de förstorade ciklarna innehåller icke-primitiva pythagoreiska tripplar.
Om ett heltal kan representeras som en summa av två kvadrater, så kan vi
I föregående del avslöjade vi processen med vilken vi kan förstora koordinatsystem på så sätt att de förstorade ciklarna innehåller icke-primitiva pythagoreiska tripplar.
Om ett heltal kan representeras som en summa av två kvadrater, så kan vi I del 2 såg vi att en primitiv pythagoreisk tripplel alltid kan representeras i form av rektangelareor (inuti rutnätscirklar).
Dyker det upp exakt 3 olika rekatngelareor inuti en sådan cirkel?
Nej, det kan dyka upp fler än så, vilket beror på
I del 2 såg vi att en primitiv pythagoreisk tripplel alltid kan representeras i form av rektangelareor (inuti rutnätscirklar).
Dyker det upp exakt 3 olika rekatngelareor inuti en sådan cirkel?
Nej, det kan dyka upp fler än så, vilket beror på I del 1 såg vi hur vissa pythagoreiska tripplar kunde representeras i form av areor på rektanglar inuti cirklar på rutnät. I den här delen undersöker vi huruvida detta är möjligt för alla primitiva tripplar.
Primitiva pythagoreiska tripplar
I del 1 såg vi hur vissa pythagoreiska tripplar kunde representeras i form av areor på rektanglar inuti cirklar på rutnät. I den här delen undersöker vi huruvida detta är möjligt för alla primitiva tripplar.
Primitiva pythagoreiska tripplar [kkratings]
Föreställ dig ett rutnät av punkter. Det går att hitta massvis med cirklar som går igenom några av punkterna. En av de minsta sådana cirklarna har hela 8 punkter på sin rand:
Det går även att hitta några rektanglar inuti sådana
[kkratings]
Föreställ dig ett rutnät av punkter. Det går att hitta massvis med cirklar som går igenom några av punkterna. En av de minsta sådana cirklarna har hela 8 punkter på sin rand:
Det går även att hitta några rektanglar inuti sådana Ett enkel spel med tärningar
Rekommenderas för
Förskolan, lågstadiet, mellanstadiet
Materiel
Ett spelplan (skriv ut nedan), två vanliga sexsidiga tärningar (helst av olika färger), minst 4 pjäser (från "Fia med knuff" till exempel)
Tid
Ett enkel spel med tärningar
Rekommenderas för
Förskolan, lågstadiet, mellanstadiet
Materiel
Ett spelplan (skriv ut nedan), två vanliga sexsidiga tärningar (helst av olika färger), minst 4 pjäser (från "Fia med knuff" till exempel)
Tid Rekommenderad från: 12 år
[kkratings]
Någon skickade ut sin stora godispåse runt bordet: första personen tog 1 godis, nästa tog 2, nästa tog 3 och så vidare, det vill säga nästa person tog alltid en godis mer än den föregående. Under
Rekommenderad från: 12 år
[kkratings]
Någon skickade ut sin stora godispåse runt bordet: första personen tog 1 godis, nästa tog 2, nästa tog 3 och så vidare, det vill säga nästa person tog alltid en godis mer än den föregående. Under I del 1 kom vi fram till att en växt inte bör växa med en rationell vinkel. Det vill säga, om vinkeln bladen emellan är 360/(p/q), så kommer växter sabba solljuset för sig själv efter p blad.
Om p=5 och q=2 så växer bladen ut med 360/(5/2)= 144
I del 1 kom vi fram till att en växt inte bör växa med en rationell vinkel. Det vill säga, om vinkeln bladen emellan är 360/(p/q), så kommer växter sabba solljuset för sig själv efter p blad.
Om p=5 och q=2 så växer bladen ut med 360/(5/2)= 144 Hur kommer det sig att det finns spiraler på kottar, kronärtskockor och ananaser? Om du inte har sett förklaringen, rekommenderar jag Vi Harts videoserie "Spirals, Fibonacci, and Being a Plant": del 1, del 2 och del 3.
(Eller kolla upp en sida på
Hur kommer det sig att det finns spiraler på kottar, kronärtskockor och ananaser? Om du inte har sett förklaringen, rekommenderar jag Vi Harts videoserie "Spirals, Fibonacci, and Being a Plant": del 1, del 2 och del 3.
(Eller kolla upp en sida på  Rekommenderad från: 11 år
[kkratings]
Måla rutorna i figuren nedan i 5 färger på så sätt att rutorna i varje rad, varje kolonn, samt varje markerad 5-rutig figur blir olikafärgade.
Visa lösningen
Man kan börja måla en hel
Rekommenderad från: 11 år
[kkratings]
Måla rutorna i figuren nedan i 5 färger på så sätt att rutorna i varje rad, varje kolonn, samt varje markerad 5-rutig figur blir olikafärgade.
Visa lösningen
Man kan börja måla en hel Det är lätt att med experiment uppskatta volymer av olika tredimensionella kroppar: Exempelvis kan ett akvarium i from av en rätblock fyllas med vatten och sedan kan man mäta hur mycket vatten som gick åt. Samma kan göras med (ungefär) sfäriska
Det är lätt att med experiment uppskatta volymer av olika tredimensionella kroppar: Exempelvis kan ett akvarium i from av en rätblock fyllas med vatten och sedan kan man mäta hur mycket vatten som gick åt. Samma kan göras med (ungefär) sfäriska En triangel kan ju delas i delar, byggas om och bli totalt en ruta mindre, se inlägget Fibonaccitalen och gyllene snittet.
Men samma princip kan utnyttjas för att få en ruta mer av en rektangel, vilket ger oss ett utmärkt sätt att äta choklad
En triangel kan ju delas i delar, byggas om och bli totalt en ruta mindre, se inlägget Fibonaccitalen och gyllene snittet.
Men samma princip kan utnyttjas för att få en ruta mer av en rektangel, vilket ger oss ett utmärkt sätt att äta choklad Rekommenderad från: 13 år
[kkratings]
I Påskens Skönhetstävling deltog Hönan, Tuppen och Kyckligen. Varje domare röstade på en av deltagarna. Påskharen räknade att det var 59 domare, där de gav 15 röser till Hönan och Tuppen sammanlagt,
Rekommenderad från: 13 år
[kkratings]
I Påskens Skönhetstävling deltog Hönan, Tuppen och Kyckligen. Varje domare röstade på en av deltagarna. Påskharen räknade att det var 59 domare, där de gav 15 röser till Hönan och Tuppen sammanlagt, Rekommenderad från: 12 år
[kkratings]
På ett bord ligger en boksamling av barnböcker i 10 delar, uppdelade i två högar. Du får ta tag i en stapel (några av de översta böckerna i en hög, som minst en, som mest hela högen) och placera
Rekommenderad från: 12 år
[kkratings]
På ett bord ligger en boksamling av barnböcker i 10 delar, uppdelade i två högar. Du får ta tag i en stapel (några av de översta böckerna i en hög, som minst en, som mest hela högen) och placera Matematik används inte bara när man ska skära upp pizza, utan också när man ska äta den. Möjligen har ni löst problemet nedan utan att ens tänka på matte.
När en pizzabit tas ut ur kartongen ser det ofta ut så här:
Mot detta finns följande
Matematik används inte bara när man ska skära upp pizza, utan också när man ska äta den. Möjligen har ni löst problemet nedan utan att ens tänka på matte.
När en pizzabit tas ut ur kartongen ser det ofta ut så här:
Mot detta finns följande Geometri är inte bara någonting skäggiga greker höll på med, utan den kan vara användbar även för den gemene svensken - till exempel när man ska dela en rund pizza!
Om man får en pizza hemkörd och ska dela den på två personer, så brukar man skära
Geometri är inte bara någonting skäggiga greker höll på med, utan den kan vara användbar även för den gemene svensken - till exempel när man ska dela en rund pizza!
Om man får en pizza hemkörd och ska dela den på två personer, så brukar man skära  Rekommenderad från: 11 år
[kkratings]
Min bror ställer in datumet varje dag med hjälp av fem träblock.
Tre av dem är av avlånga och används för månaderna.
De andra två är kuber. Vilka siffror kan stå på kubernas sidor
Rekommenderad från: 11 år
[kkratings]
Min bror ställer in datumet varje dag med hjälp av fem träblock.
Tre av dem är av avlånga och används för månaderna.
De andra två är kuber. Vilka siffror kan stå på kubernas sidor Du har säkert bilder eller monument där någon tycks följa dig med ögonen när du passerar. Men har du någonsin träffat en konstgjord varelse som följer dig med hela huvudet?
(Vänta ett tag innan videon laddas, det är värt
Du har säkert bilder eller monument där någon tycks följa dig med ögonen när du passerar. Men har du någonsin träffat en konstgjord varelse som följer dig med hela huvudet?
(Vänta ett tag innan videon laddas, det är värt Korstal 2012
[kkratings]
Fyll i precis som ett vanligt korsord (fast nu endast med siffror). Obs! Inga tal börjar med noll.
Ladda ner för utskrift.
Vågrätt:
1. Tvåpotens.
6. Siffersumman för lodrätt 13,
Korstal 2012
[kkratings]
Fyll i precis som ett vanligt korsord (fast nu endast med siffror). Obs! Inga tal börjar med noll.
Ladda ner för utskrift.
Vågrätt:
1. Tvåpotens.
6. Siffersumman för lodrätt 13, Att rita tre kvadrater
[kkratings]
Går att rita följande figur utan att lyfta pennan från pappret? Det är inte tillåtet att dra samma sträcka flera gånger.
Visa lösningen
Ja, det går! Följ bara pilarna med
Att rita tre kvadrater
[kkratings]
Går att rita följande figur utan att lyfta pennan från pappret? Det är inte tillåtet att dra samma sträcka flera gånger.
Visa lösningen
Ja, det går! Följ bara pilarna med Val i Bananrepubliken
[kkratings]
I riksdagsvalet i Bananrepubliken deltog alla landets medborgare. Alla som röstade på Clementinpartiet tycker om clementiner. Bland dem som röstade på de andra partierna tycker 90% inte
Val i Bananrepubliken
[kkratings]
I riksdagsvalet i Bananrepubliken deltog alla landets medborgare. Alla som röstade på Clementinpartiet tycker om clementiner. Bland dem som röstade på de andra partierna tycker 90% inte Kryssa grannrutor
[kkratings]
Chiyen satte ett kryss i en ruta på en rektangel. Esteban får sätta kryss i de andra rutorna, men bara om de uppfyller följande regel: man får bara kryssa i rutor som har ett udda antal
Kryssa grannrutor
[kkratings]
Chiyen satte ett kryss i en ruta på en rektangel. Esteban får sätta kryss i de andra rutorna, men bara om de uppfyller följande regel: man får bara kryssa i rutor som har ett udda antal Bilar i Mexico
[kkratings]
Mexico bestämde sig för att införa en ny lag, som innebär att varje bil i landet måste stå obrukad minst en dag i veckan (ägaren måste meddela polisen vad registreringsnumret är och vilken
Bilar i Mexico
[kkratings]
Mexico bestämde sig för att införa en ny lag, som innebär att varje bil i landet måste stå obrukad minst en dag i veckan (ägaren måste meddela polisen vad registreringsnumret är och vilken Rubiks kub utan hörn
[kkratings]
Man tog bort alla hörn från en Rubiks kub. Skulle en sådan konstruktion kunna sättas ihop av rätblock med 1x3-kuber?
Visa lösningen
Det går inte, eftersom antalet småkuber som
Rubiks kub utan hörn
[kkratings]
Man tog bort alla hörn från en Rubiks kub. Skulle en sådan konstruktion kunna sättas ihop av rätblock med 1x3-kuber?
Visa lösningen
Det går inte, eftersom antalet småkuber som Tretton punkter
[kkratings]
Dra fem streck utan att lyfta pennan från pappret så att strecken går igenom alla 13 punkterna:
Visa lösningen
Tricket är att gå utanför figuren som punkterna bildar:
Tretton punkter
[kkratings]
Dra fem streck utan att lyfta pennan från pappret så att strecken går igenom alla 13 punkterna:
Visa lösningen
Tricket är att gå utanför figuren som punkterna bildar:
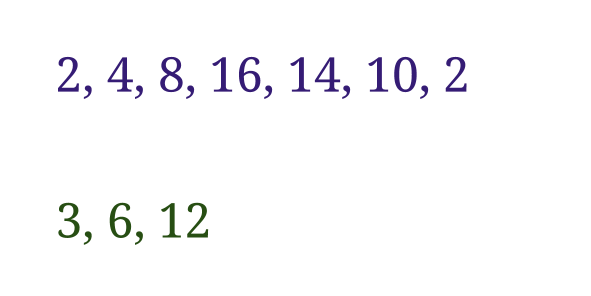 Följder med regel
[kkratings]
Du får se två följder med tal:
Det finns en regel som utifrån varje tal bestämmer nästa tal.
(a) Vad är det för regel?
(b) Bestäm alla positiva heltal som enligt regeln blir sig
Följder med regel
[kkratings]
Du får se två följder med tal:
Det finns en regel som utifrån varje tal bestämmer nästa tal.
(a) Vad är det för regel?
(b) Bestäm alla positiva heltal som enligt regeln blir sig Trapets till en triangel
[kkratings]
Dela upp figuren nedan i två delar som kan sättas ihop till en triangel.
Visa lösningen
Dela upp trapetset genom att dra en linje från ena hörnet till mitten av en motsatt
Trapets till en triangel
[kkratings]
Dela upp figuren nedan i två delar som kan sättas ihop till en triangel.
Visa lösningen
Dela upp trapetset genom att dra en linje från ena hörnet till mitten av en motsatt Ett tal med åtta siffror
[kkratings]
Kan man hitta på ett tal som består av 8 olika siffror, så att talet är delbart med alla siffror som ingår i det?
Visa lösningen
Låt oss anta att ett sådant tal finns.
Då
Ett tal med åtta siffror
[kkratings]
Kan man hitta på ett tal som består av 8 olika siffror, så att talet är delbart med alla siffror som ingår i det?
Visa lösningen
Låt oss anta att ett sådant tal finns.
Då  Bläckfiskarnas armar
[kkratings]
I havet bor bläckfiskar med 6, 7 eller 8 armar. De som har 7 armar ljuger alltid, medan de som har 6 eller 8 armar talar alltid anning.
Fyra bläckfiskar möttes en gång. Den blåa sade:
Bläckfiskarnas armar
[kkratings]
I havet bor bläckfiskar med 6, 7 eller 8 armar. De som har 7 armar ljuger alltid, medan de som har 6 eller 8 armar talar alltid anning.
Fyra bläckfiskar möttes en gång. Den blåa sade: Åtta liter
[kkratings]
Du befinner dig vid en å i skogen och du har två hinkar med dig: den ena rymmer 15 liter, den andra rymmer 16 liter. Kan du mäta upp exakt 8 liter vatten? Hinkarna saknar några som helst
Åtta liter
[kkratings]
Du befinner dig vid en å i skogen och du har två hinkar med dig: den ena rymmer 15 liter, den andra rymmer 16 liter. Kan du mäta upp exakt 8 liter vatten? Hinkarna saknar några som helst Julklappen i lådan
[kkratings]
En julklapp ligger i en låda med kvadratisk bas. Lådans höjd är hälften så långt som basens sida. Man kan linda ett 156 cm långt snöre runt lådan och göra en rosett som på bilden till vänster.
Julklappen i lådan
[kkratings]
En julklapp ligger i en låda med kvadratisk bas. Lådans höjd är hälften så långt som basens sida. Man kan linda ett 156 cm långt snöre runt lådan och göra en rosett som på bilden till vänster.  Figur i tre delar
[kkratings]
Dela upp figuren nedan i tre likadana delar.
Visa lösningen
Figur i tre delar
[kkratings]
Dela upp figuren nedan i tre likadana delar.
Visa lösningen
 En kung som gillade att bygga
[kkratings]
I Sagolandet fanns en kung som tyckte mycket om att bygga. En gång bestämde han sig för att bygga 6 torn och anlägga vägar mellan varje par av torn, men på så sätt
att det bara
En kung som gillade att bygga
[kkratings]
I Sagolandet fanns en kung som tyckte mycket om att bygga. En gång bestämde han sig för att bygga 6 torn och anlägga vägar mellan varje par av torn, men på så sätt
att det bara Egentillverkad tärning
[kkratings]
Lars tillverkade en tärning, där han satte ut 1, 2, 3, 4, 5 respektive 6 prickar på sidorna. Sedan kastade han tärningen två gånger. Första gången blev summan av alla prickar på de fyra
Egentillverkad tärning
[kkratings]
Lars tillverkade en tärning, där han satte ut 1, 2, 3, 4, 5 respektive 6 prickar på sidorna. Sedan kastade han tärningen två gånger. Första gången blev summan av alla prickar på de fyra Uppdelad rektangel
[kkratings]
En rektangel är uppdelad i 6 kvadrater (se bilden nedan). Hur stor är den största kvadraten om den minsta har sidlängden 1cm?
Obs! Figuren är inte nödvändigvis perfekt, därför räknas det inte
Uppdelad rektangel
[kkratings]
En rektangel är uppdelad i 6 kvadrater (se bilden nedan). Hur stor är den största kvadraten om den minsta har sidlängden 1cm?
Obs! Figuren är inte nödvändigvis perfekt, därför räknas det inte  Fyra lika kompisar
[kkratings]
Fyra kompisar är lika varandra på många sätt: vilket par av dem man än tittar på, så har det paret samma tilltalsnamn eller samma efternamn eller samma födelsedatum. Däremot har inga tre av
Fyra lika kompisar
[kkratings]
Fyra kompisar är lika varandra på många sätt: vilket par av dem man än tittar på, så har det paret samma tilltalsnamn eller samma efternamn eller samma födelsedatum. Däremot har inga tre av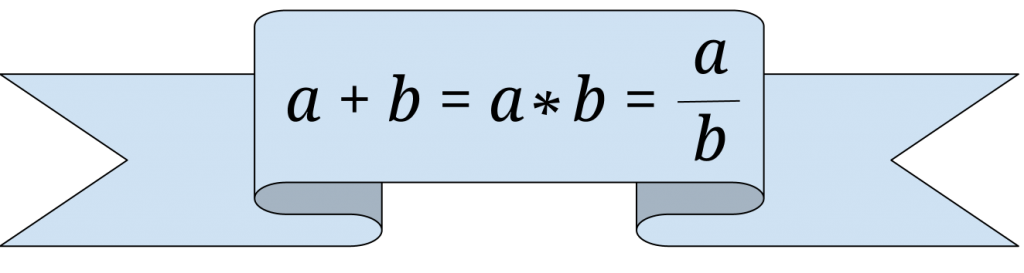 Två magiska tal
[kkratings]
Finns det två tal, sådana att deras summa, produkt, samt kvot sammanfaller?
Visa lösningen
Antag att sådana två magiska tal a och b existerar.
Om a*b = a/b, så måste a*b*b = a.
Två magiska tal
[kkratings]
Finns det två tal, sådana att deras summa, produkt, samt kvot sammanfaller?
Visa lösningen
Antag att sådana två magiska tal a och b existerar.
Om a*b = a/b, så måste a*b*b = a. Aktiviteten trassel
Rekommenderas för: gymnasieet, universitetet (eller i förenklad form för högstadiet)
Materiel: två stora rep eller sladdar (gärna av olika färger), en ogenomskinlig plastpåse
Tid: 45 minuter
Antalet deltagare: 4 + publik
Aktiviteten trassel
Rekommenderas för: gymnasieet, universitetet (eller i förenklad form för högstadiet)
Materiel: två stora rep eller sladdar (gärna av olika färger), en ogenomskinlig plastpåse
Tid: 45 minuter
Antalet deltagare: 4 + publik En alien med 4 fingrar och en människa möter varandra:
Vad är en bas?
De flesta förstår räkning med olika baser utan att behöva lära sig någon formell definition. Vi räknar i bas 10 och det finns ental, tiotal, hundratal och så vidare. Vi
En alien med 4 fingrar och en människa möter varandra:
Vad är en bas?
De flesta förstår räkning med olika baser utan att behöva lära sig någon formell definition. Vi räknar i bas 10 och det finns ental, tiotal, hundratal och så vidare. Vi Enligt en broinskription (se bilden nedan) upptäcktes kvaternionerna för exakt 169 år sedan, då William Hamilton tog en promenad i Dublin med sin fru. Hamilton kände till de komplexa talen (till exempel talet $$i$$ som uppfyller likheten $$i\cdot i
Enligt en broinskription (se bilden nedan) upptäcktes kvaternionerna för exakt 169 år sedan, då William Hamilton tog en promenad i Dublin med sin fru. Hamilton kände till de komplexa talen (till exempel talet $$i$$ som uppfyller likheten $$i\cdot i Rekommenderad från: 12 år
[kkratings]
Aladdin vill komma in i grottan, men dörren än stängd. Innanför grottan finns en tunna med fyra hål (hålen är likadana och är placerade som hörnen på en kvadrat). I varje hål finns en karaff med
Rekommenderad från: 12 år
[kkratings]
Aladdin vill komma in i grottan, men dörren än stängd. Innanför grottan finns en tunna med fyra hål (hålen är likadana och är placerade som hörnen på en kvadrat). I varje hål finns en karaff med Matematiken är full av vackra oväntade kopplingar, som mellan ett träd av bråk och ett gammalt taluppdelningsproblem.
Hittills har vi konstaterat att antalet sätt att dela upp ett tal i en summa av tvåpotenser, där ingen potens förekommer fler
Matematiken är full av vackra oväntade kopplingar, som mellan ett träd av bråk och ett gammalt taluppdelningsproblem.
Hittills har vi konstaterat att antalet sätt att dela upp ett tal i en summa av tvåpotenser, där ingen potens förekommer fler År 1858 ställde tyska matematiker Stern och Moritz en fråga: På hur många sätt kan man skriva talet n som en summa av tvåpotenser, där var tvåpotens får förekomma högst två gånger? (Ordningen på termerna i summan spelar inte någon roll).
Till
År 1858 ställde tyska matematiker Stern och Moritz en fråga: På hur många sätt kan man skriva talet n som en summa av tvåpotenser, där var tvåpotens får förekomma högst två gånger? (Ordningen på termerna i summan spelar inte någon roll).
Till Det är sällan som nya matematiska upptäckter handlar om någonting enkelt. All matematik som lärs ut i grundskolan upptäcktes för länge sedan av gamla greker, araber, kineser och indier. Gymnasiematematiken baserar sig på upptäckter som är minst 300
Det är sällan som nya matematiska upptäckter handlar om någonting enkelt. All matematik som lärs ut i grundskolan upptäcktes för länge sedan av gamla greker, araber, kineser och indier. Gymnasiematematiken baserar sig på upptäckter som är minst 300 Kvalomgången i Skolornas matematiktävling sker imorgon. Om du vill fräscha upp era geometrikunskaper inför tävlingen
här står det korfattat vad du behöver plugga på. Notera att minst ett av problemen på tävlingen är ett klassiskt
Kvalomgången i Skolornas matematiktävling sker imorgon. Om du vill fräscha upp era geometrikunskaper inför tävlingen
här står det korfattat vad du behöver plugga på. Notera att minst ett av problemen på tävlingen är ett klassiskt Skolornas matematiktävling närmar sig med stormsteg, nu är det bara en vecka kvar! Jag har skrivit tips inför tävlingen förut, men om du träna på verkliga problem, rekommenderar jag att kolla på vår cirkellektion, som handlade just om delbarhet,
Skolornas matematiktävling närmar sig med stormsteg, nu är det bara en vecka kvar! Jag har skrivit tips inför tävlingen förut, men om du träna på verkliga problem, rekommenderar jag att kolla på vår cirkellektion, som handlade just om delbarhet, Talen på formen $^n$$ dyker upp på många ställen. Finns det en cell som fördubblar sig varje minut, så finns det efter en minut 2 celler. Efter ytterligare en minut finns det 4 celler, sedan 8, sedan 16, 32, 64, 128...
Väldigt ofta dyker även
Talen på formen $^n$$ dyker upp på många ställen. Finns det en cell som fördubblar sig varje minut, så finns det efter en minut 2 celler. Efter ytterligare en minut finns det 4 celler, sedan 8, sedan 16, 32, 64, 128...
Väldigt ofta dyker även Tack till Lisa Lokteva för att hon tipsade mig om nedanstående problem:
Rekommenderad från: 15 år
[kkratings]
Två personer anländer oberoende av varandra till en bestämd plats mellan 9.30 och 10.00. De stannar på platsen i exakt tre
Tack till Lisa Lokteva för att hon tipsade mig om nedanstående problem:
Rekommenderad från: 15 år
[kkratings]
Två personer anländer oberoende av varandra till en bestämd plats mellan 9.30 och 10.00. De stannar på platsen i exakt tre  Har du alltid velat att rita egna fraktaler, men inte vetat hur man gör?
Grundprincipen för en fraktal är ett mönster som upprepar sig inuti figuren om och om igen. De mest kända exempel är:
Sierpinskis triangel
En liksidig triangel delas
Har du alltid velat att rita egna fraktaler, men inte vetat hur man gör?
Grundprincipen för en fraktal är ett mönster som upprepar sig inuti figuren om och om igen. De mest kända exempel är:
Sierpinskis triangel
En liksidig triangel delas  De flesta människor tycker inte om algebra i skolan. Utan någon intuition för vad som händer tvingas de att lösa ekvationer i skolan. Och när ekvationen väl är löst finns det ingen känsla av tillfredsställning, snarare kvarstår förvirringen och
De flesta människor tycker inte om algebra i skolan. Utan någon intuition för vad som händer tvingas de att lösa ekvationer i skolan. Och när ekvationen väl är löst finns det ingen känsla av tillfredsställning, snarare kvarstår förvirringen och Den senaste träffen på Katedralskolan genomförde vi en liten tävling bland deltagarna.
Varje deltagare fick 5 stycken problem att lösa på kort tid. Dock behövde inte problemen lösas fullständigt, utan det viktiga var att uppnå ett resultat. Men
Den senaste träffen på Katedralskolan genomförde vi en liten tävling bland deltagarna.
Varje deltagare fick 5 stycken problem att lösa på kort tid. Dock behövde inte problemen lösas fullständigt, utan det viktiga var att uppnå ett resultat. Men Den här vårterminen har jag äran att tillsammans med en annan lärare leda problemlösningskursen på Katedralskolan i Uppsala! Vi håller 2 timmarslektioner för intresserade elever på skolan, samt för nior som ska börja läsa där.
Tanken med träffarna
Den här vårterminen har jag äran att tillsammans med en annan lärare leda problemlösningskursen på Katedralskolan i Uppsala! Vi håller 2 timmarslektioner för intresserade elever på skolan, samt för nior som ska börja läsa där.
Tanken med träffarna Rekommenderad från: 15 år
[kkratings]
En polisstation befinner sig på en väg som sträcker sig oändligt långt åt båda håll. Någon stal den gamla polisbilen, som har maxhastigheten lika med 90% av den nya polisbilens
Rekommenderad från: 15 år
[kkratings]
En polisstation befinner sig på en väg som sträcker sig oändligt långt åt båda håll. Någon stal den gamla polisbilen, som har maxhastigheten lika med 90% av den nya polisbilens Rekommenderad från: 12 år
[kkratings]
Någon antecknade fiskens bana i ett akvarium sett framifrån (första bilden) och någon annan ritade banan sett högerifrån (andra bilden). Hur såg fiskens bana ut om man kollade
Rekommenderad från: 12 år
[kkratings]
Någon antecknade fiskens bana i ett akvarium sett framifrån (första bilden) och någon annan ritade banan sett högerifrån (andra bilden). Hur såg fiskens bana ut om man kollade Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.
Här kan du se vad vi tidigare har gått igenom.
Mönster
Väldigt mycket i
Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.
Här kan du se vad vi tidigare har gått igenom.
Mönster
Väldigt mycket i Rekommenderad från: 10 år
[kkratings]
Siffrorna 1 till 9 fyller kvadraten som det syns på den vänstra bilden. Man får gå på kvadratens rutor, men aldrig tillbaka till en ruta man varit på förut, och man måste alltid gå till en
Rekommenderad från: 10 år
[kkratings]
Siffrorna 1 till 9 fyller kvadraten som det syns på den vänstra bilden. Man får gå på kvadratens rutor, men aldrig tillbaka till en ruta man varit på förut, och man måste alltid gå till en Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.
Här kan du se vad vi tidigare har gått igenom.
Grafer
Jag försökte att
Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.
Här kan du se vad vi tidigare har gått igenom.
Grafer
Jag försökte att Grattis på pidagen!
Rekommenderad från: 17 år
Förkunskaper: radianer, transformationer.
[kkratings]
Ett lejon springer runt på en rund cirkusarena, som har radien 10 m. Lejonets bana består av raka streck och i slutändan springer
Grattis på pidagen!
Rekommenderad från: 17 år
Förkunskaper: radianer, transformationer.
[kkratings]
Ett lejon springer runt på en rund cirkusarena, som har radien 10 m. Lejonets bana består av raka streck och i slutändan springer Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.
Här kan du se vad vi tidigare har gått igenom.
Fyrhörningar
Vad är en
Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.
Här kan du se vad vi tidigare har gått igenom.
Fyrhörningar
Vad är en Rekommenderad från: 12 år
[kkratings]
Invånarna på Matteön delar in dygnet i timmar, timmar i några minuter och minuter i några sekunder. Men deras dygn består av 77 minuter och deras timme innehåller 91 sekunder. Hur många sekunder
Rekommenderad från: 12 år
[kkratings]
Invånarna på Matteön delar in dygnet i timmar, timmar i några minuter och minuter i några sekunder. Men deras dygn består av 77 minuter och deras timme innehåller 91 sekunder. Hur många sekunder Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.
Här kan du se vad vi tidigare har gått igenom.
Kombinatorik
Kombinatorik är
Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.
Här kan du se vad vi tidigare har gått igenom.
Kombinatorik
Kombinatorik är [kkratings]
I en vägg sitter tjugo spikar (se bilden). Avståndet mellan två spikar som sitter precis bredvid varandra är 1 cm.
Din uppgift är att spänna en 19 cm lång tråd mellan spik 1 och spik 2, så att den går igenom alla
[kkratings]
I en vägg sitter tjugo spikar (se bilden). Avståndet mellan två spikar som sitter precis bredvid varandra är 1 cm.
Din uppgift är att spänna en 19 cm lång tråd mellan spik 1 och spik 2, så att den går igenom alla Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.
Notera att barnen redan har haft två lektioner om vinklar och olika
Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.
Notera att barnen redan har haft två lektioner om vinklar och olika [kkratings]
På en gymnasieskola tillfrågade man alla elever om vilka språk de kunde. Det visade sig att fler än 90% kunde både engelska och tyska, samt att fler än 90% kunde både engelska och franska.
Visa att bland de elever som
[kkratings]
På en gymnasieskola tillfrågade man alla elever om vilka språk de kunde. Det visade sig att fler än 90% kunde både engelska och tyska, samt att fler än 90% kunde både engelska och franska.
Visa att bland de elever som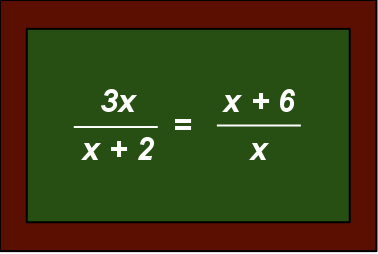 Nyligen pratade jag med en kollega om ekvationer. Att så pass måna barn och ungdomar i Sverige har svårt att förstå hur ekvationer funkar.
En möjlig förklaring till detta är att det blir för stort hopp i abstrakt tänkande när ekvationer först
Nyligen pratade jag med en kollega om ekvationer. Att så pass måna barn och ungdomar i Sverige har svårt att förstå hur ekvationer funkar.
En möjlig förklaring till detta är att det blir för stort hopp i abstrakt tänkande när ekvationer först Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.
Notera att barnen redan har haft en introduktion till vinklar och olika
Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.
Notera att barnen redan har haft en introduktion till vinklar och olika [kkratings]
Två spelare spelar på ett oregelbundet rutigt bräde. De turas om att flytta pjäsen Centauren, som kan flyttas antingen en ruta åt vänster, en ruta uppåt eller en ruta uppåt-höger på ett drag.
Spelaren som inte kan flytta
[kkratings]
Två spelare spelar på ett oregelbundet rutigt bräde. De turas om att flytta pjäsen Centauren, som kan flyttas antingen en ruta åt vänster, en ruta uppåt eller en ruta uppåt-höger på ett drag.
Spelaren som inte kan flytta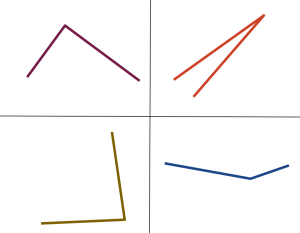 En ny termin är igång och för mig innebär det söndagsträffar med mina matematiksugna 5-, 6-, 7- och 10-åringar! Förra terminen skrev jag om våra 6 träffar, men vi har egentligen haft 11 stycken och i vår ska vi ha ungefär lika många!
Gamla
En ny termin är igång och för mig innebär det söndagsträffar med mina matematiksugna 5-, 6-, 7- och 10-åringar! Förra terminen skrev jag om våra 6 träffar, men vi har egentligen haft 11 stycken och i vår ska vi ha ungefär lika många!
Gamla Lördagen den 21 januari var en spännande dag för ca 45 högstadieelever. De tävlade nämligen i junior-sm i matte, det vill säga finalen i Högstadiets Matematiktävling!
Vinnaren blev precis som förra året Lisa Lokteva från Borås, denna gång på en
Lördagen den 21 januari var en spännande dag för ca 45 högstadieelever. De tävlade nämligen i junior-sm i matte, det vill säga finalen i Högstadiets Matematiktävling!
Vinnaren blev precis som förra året Lisa Lokteva från Borås, denna gång på en Jag behåller traditionen och presenterar ett sifferkorsord även i år. Denna är lite svårare än förra året, men också lite mindre. Utmana dina nära och kära eller lös korstalet tillsammans.
God Jul önskar mattebloggen!
Mattekorsord
Jag behåller traditionen och presenterar ett sifferkorsord även i år. Denna är lite svårare än förra året, men också lite mindre. Utmana dina nära och kära eller lös korstalet tillsammans.
God Jul önskar mattebloggen!
Mattekorsord Hungrig student
[kkratings]
Pelle har en stekpanna som det får plats två hamburgare i samtidigt. Han vill steka varje hamburgare på varje sida i 2 minuter. Pelle är hungrig och vill steka tre hamburgare så fort som möjligt.
Hungrig student
[kkratings]
Pelle har en stekpanna som det får plats två hamburgare i samtidigt. Han vill steka varje hamburgare på varje sida i 2 minuter. Pelle är hungrig och vill steka tre hamburgare så fort som möjligt. Triangellandet
[kkratings]
Triangellandet har formen av en liksidig triangel. En inre gräns delar landet i två stater, som har lika stor area. Beskriv hur gränsen ser ut (formen och positionen) om den har den minsta möjliga
Triangellandet
[kkratings]
Triangellandet har formen av en liksidig triangel. En inre gräns delar landet i två stater, som har lika stor area. Beskriv hur gränsen ser ut (formen och positionen) om den har den minsta möjliga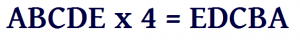 Sifferrebus
Vilka siffror passar istället för bokstäverna? (Varje bokstav är en unik siffra.)
Visa lösningen
Eftersom talet fortfarande har fem siffror efter multiplikationen, får inte A var för stort. A=1 eller A=2 fungerar. Men å andra
Sifferrebus
Vilka siffror passar istället för bokstäverna? (Varje bokstav är en unik siffra.)
Visa lösningen
Eftersom talet fortfarande har fem siffror efter multiplikationen, får inte A var för stort. A=1 eller A=2 fungerar. Men å andra Polyedrar och polygoner
[kkratings]
Visa att varje polyeder har minst två sidor som är polygoner med lika många hörn.
Visa lösningen
Antag att det finns en polyeder där alla sidor har olika antal hörn. Ta då den
Polyedrar och polygoner
[kkratings]
Visa att varje polyeder har minst två sidor som är polygoner med lika många hörn.
Visa lösningen
Antag att det finns en polyeder där alla sidor har olika antal hörn. Ta då den Kronans massa
[kkratings]
En krona som väger 60 minor (en mina är en antik viktenhet) är gjord på en legering av guld, koppar, tenn och järn. Guld och koppar utgör 2/3, guld och tenn - 3/4, guld och järn - 3/5 av hela kronans
Kronans massa
[kkratings]
En krona som väger 60 minor (en mina är en antik viktenhet) är gjord på en legering av guld, koppar, tenn och järn. Guld och koppar utgör 2/3, guld och tenn - 3/4, guld och järn - 3/5 av hela kronans  Tetris
[kkratings]
I tetris används sju brickor:
Går det att använda alla brickorna och bygga:
a) en rektangel med formen 4x7
b) en "triangel"?
Visa lösningen
Varken figur a) eller figur b) går att bygga.
Tetris
[kkratings]
I tetris används sju brickor:
Går det att använda alla brickorna och bygga:
a) en rektangel med formen 4x7
b) en "triangel"?
Visa lösningen
Varken figur a) eller figur b) går att bygga. Schackpjäs
[kkratings]
Vilken pjäs står på rutan h4 i den här schackpositionen?
Visa lösningen
Det kan inte precis ha varit svarts tur, eftersom svart kung är under schack. Alltså har vit precis gjort ett drag. Vit
Schackpjäs
[kkratings]
Vilken pjäs står på rutan h4 i den här schackpositionen?
Visa lösningen
Det kan inte precis ha varit svarts tur, eftersom svart kung är under schack. Alltså har vit precis gjort ett drag. Vit Änglarna på granen
[kkratings]
Fyra änglar sitter på en julgran bland all pynt. Två av dem hade blå glorior och två hade gula. Änglarna vet inte vem som har vilket sorts gloria, men alla vet vem som kan se vem (se
Änglarna på granen
[kkratings]
Fyra änglar sitter på en julgran bland all pynt. Två av dem hade blå glorior och två hade gula. Änglarna vet inte vem som har vilket sorts gloria, men alla vet vem som kan se vem (se Kamelen och bananerna
En kamel odlar bananer. Det här året fick han bästa skörden någonsin: 3000 bananer! Men tyvärr ligger den närmaste platsen där han kan sälja bananerna 1000 km bort. Kamelen kan bara bära 1000 bananer i taget och på vägen
Kamelen och bananerna
En kamel odlar bananer. Det här året fick han bästa skörden någonsin: 3000 bananer! Men tyvärr ligger den närmaste platsen där han kan sälja bananerna 1000 km bort. Kamelen kan bara bära 1000 bananer i taget och på vägen Triell
[kkratings]
A, B och C deltar i en triangelduell med pistoler. Alla vet att A träffar med sannolikheten 0,3. Sannolikheten att C träffar är 0,5, medan B missar aldrig. Deltagarna skjuter en i taget mot en vald person
Triell
[kkratings]
A, B och C deltar i en triangelduell med pistoler. Alla vet att A träffar med sannolikheten 0,3. Sannolikheten att C träffar är 0,5, medan B missar aldrig. Deltagarna skjuter en i taget mot en vald person Ålder
[kkratings]
En man fick frågan: "Hur gammal är du?" Han svarade: "Jag är ganska gammal. Jag är sexhundra gånger äldre är några av mina släktingar."
Kan mannen tala sanning?
Visa lösningen
Ja, det kan vara
Ålder
[kkratings]
En man fick frågan: "Hur gammal är du?" Han svarade: "Jag är ganska gammal. Jag är sexhundra gånger äldre är några av mina släktingar."
Kan mannen tala sanning?
Visa lösningen
Ja, det kan vara Ett väldigt delbart tal
[kkratings]
Talet 310 är delbart med både 31 och 10. Hitta på ett så stort tal som möjligt, som är delbart med alla tvåsiffriga tal som grannsiffrorna i talet utgör. Det är inte tillåtet att ha nollor inuti
Ett väldigt delbart tal
[kkratings]
Talet 310 är delbart med både 31 och 10. Hitta på ett så stort tal som möjligt, som är delbart med alla tvåsiffriga tal som grannsiffrorna i talet utgör. Det är inte tillåtet att ha nollor inuti  En heltalskub
[kkratings]
För en viss kub räknade man ut följande tre tal: summan av alla sidlängder, ytan, samt volymen. Alla talen, uttryckta i centimeter/kvadratcentimeter/kubikcentimeter, är tresiffriga heltal. Hur lång
En heltalskub
[kkratings]
För en viss kub räknade man ut följande tre tal: summan av alla sidlängder, ytan, samt volymen. Alla talen, uttryckta i centimeter/kvadratcentimeter/kubikcentimeter, är tresiffriga heltal. Hur lång Ett till logikproblem till alla!
Test utan text
[kkratings]
Camelia pluggade hårt inför ett test. Hon kollade på frågorna och svaren på förra årets test, men upptäckte att en av frågorna blev dåligt utskriven. Svaren syntes
Ett till logikproblem till alla!
Test utan text
[kkratings]
Camelia pluggade hårt inför ett test. Hon kollade på frågorna och svaren på förra årets test, men upptäckte att en av frågorna blev dåligt utskriven. Svaren syntes  Kanske har du hört problemet om bonden och hans ägodelar. Det här är en annan variant på problemet!
Komma över till andra sidan
Det finns en båt med plats för tre och en av platserna är reserverad åt bonden. Bonden måste komma över till andra
Kanske har du hört problemet om bonden och hans ägodelar. Det här är en annan variant på problemet!
Komma över till andra sidan
Det finns en båt med plats för tre och en av platserna är reserverad åt bonden. Bonden måste komma över till andra Vattenmelon
[kkratings]
En nyköpt vattenmelon vägde 10 kilogram och bestod till 99% av av vatten. Efter ett tag torkade den ut och nu består den till 98% av vatten. Hur mycket väger vattenmelonen nu?
Visa
Vattenmelon
[kkratings]
En nyköpt vattenmelon vägde 10 kilogram och bestod till 99% av av vatten. Efter ett tag torkade den ut och nu består den till 98% av vatten. Hur mycket väger vattenmelonen nu?
Visa Ädelstenar
[kkratings]
Dario fick en stor säck i julklapp av en väldigt rik person. I säcken ligger sjukt många ädelstenar, gröna och gula, men han kan inte avgöra på formen vilken färg de har. Dario tar ut 100 ädelstenar på
Ädelstenar
[kkratings]
Dario fick en stor säck i julklapp av en väldigt rik person. I säcken ligger sjukt många ädelstenar, gröna och gula, men han kan inte avgöra på formen vilken färg de har. Dario tar ut 100 ädelstenar på Dagens gåta är en sifferrebus. Notera att trigonometriska "formeln" inte stämmer.
Trigonometrisk rebus
[kkratings]
Kevin ställde upp en addition, men sedan döljde uträkningen genom att byta ut siffror mot bokstäver
Dagens gåta är en sifferrebus. Notera att trigonometriska "formeln" inte stämmer.
Trigonometrisk rebus
[kkratings]
Kevin ställde upp en addition, men sedan döljde uträkningen genom att byta ut siffror mot bokstäver Bräde
[kkratings]
Ett bräde är indelad i 4x4 rutor. Du får såga längs med de små rutdiagonalerna (det går bra att såga i båda diagonalerna på en vissa ruta). Hur många små diagonaler kan du som mest såga utan att brädet faller
Bräde
[kkratings]
Ett bräde är indelad i 4x4 rutor. Du får såga längs med de små rutdiagonalerna (det går bra att såga i båda diagonalerna på en vissa ruta). Hur många små diagonaler kan du som mest såga utan att brädet faller Rektangel
[kkratings]
Du har tillgång till 12 sträckor som är 2cm långa, 12 sträckor som är 3cm och 11 sträckor med längden 5cm. Går det att bygga en rektangel av alla sträckorna med sidlängderna lika med ett helt antal
Rektangel
[kkratings]
Du har tillgång till 12 sträckor som är 2cm långa, 12 sträckor som är 3cm och 11 sträckor med längden 5cm. Går det att bygga en rektangel av alla sträckorna med sidlängderna lika med ett helt antal Tre brev
Du har fått tre brev och måste omedelbart äta upp ett av dem. I varje brev finns en lapp med två meningar. I ett av breven är båda meningarna goda råd, i ett annat är båda dåliga råd och det tredje innehåller ett gott och ett dåligt
Tre brev
Du har fått tre brev och måste omedelbart äta upp ett av dem. I varje brev finns en lapp med två meningar. I ett av breven är båda meningarna goda råd, i ett annat är båda dåliga råd och det tredje innehåller ett gott och ett dåligt Femkronors-spel
Erik och Sixten spelar ett spel mot varandra. Reglerna är enkla: de turas om att lägga femkronors-mynt på ett runt bord (som från början är tomt). Mynten som redan är lagda ligger kvar till slutet av spelet. Den pojken, som inte
Femkronors-spel
Erik och Sixten spelar ett spel mot varandra. Reglerna är enkla: de turas om att lägga femkronors-mynt på ett runt bord (som från början är tomt). Mynten som redan är lagda ligger kvar till slutet av spelet. Den pojken, som inte I helgen har Sonja Kovalevsky-dagarna varit i Stockholm för andra året i rad. Och fjärde året i rad har jag hjälpt till med problemlösningsdelen :)
Här är tävlingsproblemen och lösningar för de
I helgen har Sonja Kovalevsky-dagarna varit i Stockholm för andra året i rad. Och fjärde året i rad har jag hjälpt till med problemlösningsdelen :)
Här är tävlingsproblemen och lösningar för de Jag fortsätter mina lektioner med små barn i Stockholm. Läs om de föregående träffarna:
1 & 2
3 & 4
eller fortsätt läsa det här inlägget. Notera att ordningen inte är kronologisk och att inte alla aktiviteter förekommer på alla
Jag fortsätter mina lektioner med små barn i Stockholm. Läs om de föregående träffarna:
1 & 2
3 & 4
eller fortsätt läsa det här inlägget. Notera att ordningen inte är kronologisk och att inte alla aktiviteter förekommer på alla Jag fortsätter mina lektioner med små barn i Stockholm. Läs om de första två träffarna eller fortsätt läsa det här inlägget. Notera att ordningen inte är kronologisk och att inte alla aktiviteter förekommer på alla lektioner.
Geometri för
Jag fortsätter mina lektioner med små barn i Stockholm. Läs om de första två träffarna eller fortsätt läsa det här inlägget. Notera att ordningen inte är kronologisk och att inte alla aktiviteter förekommer på alla lektioner.
Geometri för Jag hade själv länge ingen intuitiv förståelse för $$e$$. Jag visste att funktionen $$e^x$$ hade sig själv som derivata och att funktionen hade en snygg Taylorutveckling. Men inte så mycket vad det hade med naturen att göra.
Tills jag träffade på
Jag hade själv länge ingen intuitiv förståelse för $$e$$. Jag visste att funktionen $$e^x$$ hade sig själv som derivata och att funktionen hade en snygg Taylorutveckling. Men inte så mycket vad det hade med naturen att göra.
Tills jag träffade på  Denna höst har jag börjat jobba på ett helt nytt sätt. Jag undervisar fem- och sexåringar i matte i ryska klubben "Kolobok" i Stockholm! En gång i veckan träffar jag fyra grupper med barn mellan (en med femåringar, två med sexåringar och en med
Denna höst har jag börjat jobba på ett helt nytt sätt. Jag undervisar fem- och sexåringar i matte i ryska klubben "Kolobok" i Stockholm! En gång i veckan träffar jag fyra grupper med barn mellan (en med femåringar, två med sexåringar och en med Året var 1997. Det var då jag började ha matematiska framgångar och blev därmed skickad på en resa till den stora staden Moskva. Där skulle jag och andra 6:or och 7:or tävla i problemlösning. Som jag minns det gick det hyfsat ok för mig, men ett
Året var 1997. Det var då jag började ha matematiska framgångar och blev därmed skickad på en resa till den stora staden Moskva. Där skulle jag och andra 6:or och 7:or tävla i problemlösning. Som jag minns det gick det hyfsat ok för mig, men ett Ett välkänt trick är att man kan klippa en triangel i bitar, arrangera om bitarna, sätta ihop dem till en triangel igen och få en extra ruta!
Hur kan det stämma? Nedan kommer förklaringen, men fundera själv
Ett välkänt trick är att man kan klippa en triangel i bitar, arrangera om bitarna, sätta ihop dem till en triangel igen och få en extra ruta!
Hur kan det stämma? Nedan kommer förklaringen, men fundera själv Ni läsarna har sagt ert, vilket resulterar i att bidrag 5 och bidrag 6 vinner tävlingen för snyggast lösning.
Det vill säga vinnarna den här våren (förutom Skägget) är Benjamin och David! Grattis, priserna ska jag skicka ut i augusti!
För min
Ni läsarna har sagt ert, vilket resulterar i att bidrag 5 och bidrag 6 vinner tävlingen för snyggast lösning.
Det vill säga vinnarna den här våren (förutom Skägget) är Benjamin och David! Grattis, priserna ska jag skicka ut i augusti!
För min  Rebusarna motsvarar filmtitlar på engelska. Försök att lista ut så många du
Rebusarna motsvarar filmtitlar på engelska. Försök att lista ut så många du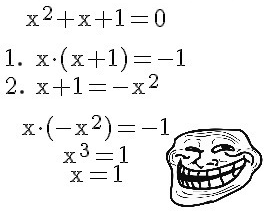 Låt oss lösa en andragradsekvation. Vi gör det inte med hjälp av pq-formeln utan på ett annat
Låt oss lösa en andragradsekvation. Vi gör det inte med hjälp av pq-formeln utan på ett annat Matchen (2 poäng).
Innan fotbollsmatchen mellan lag Syd och lag Nord fanns det 5 prognoser:
a) det kommer inte att bli oavgjort
b) Syd kommer att släppa in mål
c) Nord kommer att vinna
d) Nord kommer inte att förlora
e) det kommer bli exakt 3
Matchen (2 poäng).
Innan fotbollsmatchen mellan lag Syd och lag Nord fanns det 5 prognoser:
a) det kommer inte att bli oavgjort
b) Syd kommer att släppa in mål
c) Nord kommer att vinna
d) Nord kommer inte att förlora
e) det kommer bli exakt 3  Cthulhu (1 poäng).
"Ni alledels för små för att se detta", sade Cthulhu till sina 33 barn och skrek ut "Blunda!". Alla pojkarna blundade med högerögat, likaså en tredjedel av flickorna. Alla flickorna blundade med vänsterögat, likaså en tredjedel
Cthulhu (1 poäng).
"Ni alledels för små för att se detta", sade Cthulhu till sina 33 barn och skrek ut "Blunda!". Alla pojkarna blundade med högerögat, likaså en tredjedel av flickorna. Alla flickorna blundade med vänsterögat, likaså en tredjedel Hexagonen (1 poäng).
Fyll i rutorna i "hexagonen" nedan med heltalen från 1 till 19, så att summan av talen i varje kolonn och i varje diagonal blir densamma. Varje tal får utnyttjas exakt en gång, och vissa tal är redan på sin
Hexagonen (1 poäng).
Fyll i rutorna i "hexagonen" nedan med heltalen från 1 till 19, så att summan av talen i varje kolonn och i varje diagonal blir densamma. Varje tal får utnyttjas exakt en gång, och vissa tal är redan på sin Papper (3 poäng).
Man tog ett rektangulärt papper och vikte ihop det så att ena hörnet hamnade i mitten på kortsidan (se bilden). Det visade sig att trianglarna I och II var kongruenta.
Hur lång var papprets långsida om kortsidan var 8 cm
Papper (3 poäng).
Man tog ett rektangulärt papper och vikte ihop det så att ena hörnet hamnade i mitten på kortsidan (se bilden). Det visade sig att trianglarna I och II var kongruenta.
Hur lång var papprets långsida om kortsidan var 8 cm När jag säger "tangentlinje" tänker du kanske på någon av dessa bilder:
En tangentlinje nuddar precis en kurva i en viss punkt. Ofta har jag tänkt att en tangent aldrig är en sekant, det vill säga att tangenten aldrig kan skära kurvan.
Men
När jag säger "tangentlinje" tänker du kanske på någon av dessa bilder:
En tangentlinje nuddar precis en kurva i en viss punkt. Ofta har jag tänkt att en tangent aldrig är en sekant, det vill säga att tangenten aldrig kan skära kurvan.
Men  Nu kommer de svåraste problemen hittills! Nästa vecka återkommer jag till normal svårighetsgrad.
Skicka in lösningsförslag genom att klicka på länken under uppgifterna senast måndagen den 28 mars. Glöm inte att kolla reglerna och aktuella
Nu kommer de svåraste problemen hittills! Nästa vecka återkommer jag till normal svårighetsgrad.
Skicka in lösningsförslag genom att klicka på länken under uppgifterna senast måndagen den 28 mars. Glöm inte att kolla reglerna och aktuella Skicka in lösningsförslag genom att klicka på länken under uppgifterna senast måndagen den 21 mars. Glöm inte att kolla reglerna och aktuella poängställningen.
Blommor (2 poäng). Längs med vägen mellan Kalles och Kajsas stugor växte blommor på
Skicka in lösningsförslag genom att klicka på länken under uppgifterna senast måndagen den 21 mars. Glöm inte att kolla reglerna och aktuella poängställningen.
Blommor (2 poäng). Längs med vägen mellan Kalles och Kajsas stugor växte blommor på Försök att lösa! Som vanligt ska varje stor ruta, varje rad och varje kolumn innehålla alla 9 siffrorna en gång
Försök att lösa! Som vanligt ska varje stor ruta, varje rad och varje kolumn innehålla alla 9 siffrorna en gång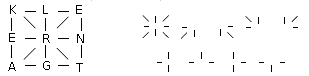 Skicka in lösningsförslag genom att klicka på länken under uppgifterna senast måndagen den 14 mars. Glöm inte att kolla reglerna och aktuella poängställningen.
Rebusen (1 poäng). Försök att läsa av ordet genom att använda
Skicka in lösningsförslag genom att klicka på länken under uppgifterna senast måndagen den 14 mars. Glöm inte att kolla reglerna och aktuella poängställningen.
Rebusen (1 poäng). Försök att läsa av ordet genom att använda Kuben (1 poäng). En träkub har sidlängden 1 m. Vi sågar upp kuben i små kuber som alla har sidlängden 1 cm och lägger alla småkuberna på en rad. Hur lång blir raden?
Siffertriangeln (3 poäng). Går det att fylla de gula cirklarna med siffrorna
Kuben (1 poäng). En träkub har sidlängden 1 m. Vi sågar upp kuben i små kuber som alla har sidlängden 1 cm och lägger alla småkuberna på en rad. Hur lång blir raden?
Siffertriangeln (3 poäng). Går det att fylla de gula cirklarna med siffrorna Baserat på första lektionen, har jag gjort en presentation om potenser. Drygt hälften av föredraget kommer från den första lektionen jag lade upp, men resten är utfyllt med mer material om potenser. Se för er själva!
Lektion om potenser - tog
Baserat på första lektionen, har jag gjort en presentation om potenser. Drygt hälften av föredraget kommer från den första lektionen jag lade upp, men resten är utfyllt med mer material om potenser. Se för er själva!
Lektion om potenser - tog .advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;
.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;  .advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;
.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;  .advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;
.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;  .advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;
.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;  .advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;
.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;  .advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;
.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;  .advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;
.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;  .advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;
.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;  .advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;
.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;  .advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;
.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px 5px;  .advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px
.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px .advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px
.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px .problemly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.problemlly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px
.problemly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.problemlly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 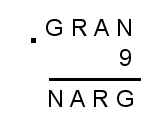 .advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px
.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px .advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px
.advent {
padding: 0px 5px; margin: 0 auto; background: url(http://mattebloggen.com/wp-content/uploads/2010/11/flinga.png) repeat; -moz-border-radius: 10px; border-radius: 10px; height: 30px; width: 100%;
}
.adventsgata {
padding: 5px .problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 10px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;
.problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 10px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto; .problemly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.problemlly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px
.problemly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.problemlly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px  .problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 10px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;
.problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 10px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto; .problemy45 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #BBEE99; -moz-border-radius: 10px; border-radius: 10px;
}
.equation {
padding: 0px 0px; border: 3px solid #526B7F;
}
.problemy45 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #BBEE99; -moz-border-radius: 10px; border-radius: 10px;
}
.equation {
padding: 0px 0px; border: 3px solid #526B7F;
}
 .problemly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.problemlly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px
.problemly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.problemlly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px  .problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 10px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;
.problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 10px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto; Äntligen är de här, lösningarna till problemen som eleverna tävlade i under Sonja Kovalevsky-dagarna 2010!
Lösningar till alla 15
Äntligen är de här, lösningarna till problemen som eleverna tävlade i under Sonja Kovalevsky-dagarna 2010!
Lösningar till alla 15 För tredje gången i rad var jag med och ordnade problemlösning (tillsammans med Dag Jonsson, Magnus Carlson och min pappa) på Sonja Kovalevsky-dagarna. Tredje gånget gillt verkar det som.
Dessa dagar har som syfte att visa varför det är bra
För tredje gången i rad var jag med och ordnade problemlösning (tillsammans med Dag Jonsson, Magnus Carlson och min pappa) på Sonja Kovalevsky-dagarna. Tredje gånget gillt verkar det som.
Dessa dagar har som syfte att visa varför det är bra .problemy45 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #BBEE99; -moz-border-radius: 10px; border-radius: 10px;
}
.equation {
padding: 0px 0px; border: 3px solid #526B7F;
}
.problemy45 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #BBEE99; -moz-border-radius: 10px; border-radius: 10px;
}
.equation {
padding: 0px 0px; border: 3px solid #526B7F;
}
 .problemly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.problemlly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px
.problemly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.problemlly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px  .problema45{
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #B2DCFF; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;
.problema45{
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #B2DCFF; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto; .problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 10px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;
.problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 10px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto; En mörk eftermiddag hade ett gäng studenter samlats för att kolla på - ni gissade rätt - Futurama! Ljuset släcktes, stora platt-teven
En mörk eftermiddag hade ett gäng studenter samlats för att kolla på - ni gissade rätt - Futurama! Ljuset släcktes, stora platt-teven  .problemy44 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #BBEE99; -moz-border-radius: 10px; border-radius: 10px; height: 180px;
}
.equation {
padding: 0px 0px; border: 3px solid #526B7F;
}
.problemy44 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #BBEE99; -moz-border-radius: 10px; border-radius: 10px; height: 180px;
}
.equation {
padding: 0px 0px; border: 3px solid #526B7F;
}
 .problemly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.problemlly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px
.problemly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.problemlly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px  .problema44{
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #B2DCFF; -moz-border-radius: 10px; border-radius: 10px; height: 220px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0
.problema44{
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #B2DCFF; -moz-border-radius: 10px; border-radius: 10px; height: 220px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0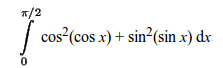 .problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 10px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;
.problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 10px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto; .problemy42 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #BBEE99; -moz-border-radius: 10px; border-radius: 10px;
}
.equation {
padding: 0px 0px; border: 3px solid #526B7F;
}
.problemy42 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #BBEE99; -moz-border-radius: 10px; border-radius: 10px;
}
.equation {
padding: 0px 0px; border: 3px solid #526B7F;
}
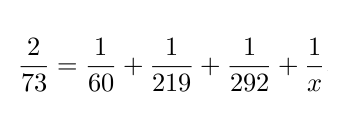 .problemly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.problemlly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px
.problemly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.problemlly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px  .problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 10px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;
.problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 10px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto; .problemy42 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #BBEE99; -moz-border-radius: 10px; border-radius: 10px;
}
.equation {
padding: 0px 0px; border: 3px solid #526B7F;
}
.problemy42 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #BBEE99; -moz-border-radius: 10px; border-radius: 10px;
}
.equation {
padding: 0px 0px; border: 3px solid #526B7F;
}
 .problemly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.problemlly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px
.problemly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.problemlly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 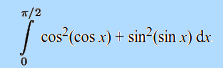 .problem{
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #B2DCFF; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;
.problem{
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #B2DCFF; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;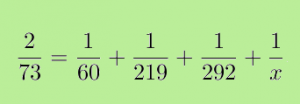 .problemy41 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #BBEE99; -moz-border-radius: 10px; border-radius: 10px; height: 200px;
}
.equation {
padding: 0px 0px; border: 3px solid #526B7F;
}
.problemy41 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #BBEE99; -moz-border-radius: 10px; border-radius: 10px; height: 200px;
}
.equation {
padding: 0px 0px; border: 3px solid #526B7F;
}
 .problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 10px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;
.problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 10px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto; .problemy36 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #BBEE99; -moz-border-radius: 10px; border-radius: 10px; height: 180px;
}
Mattegåta
En man har ett litet hål i väggen (lika stor som
.problemy36 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #BBEE99; -moz-border-radius: 10px; border-radius: 10px; height: 180px;
}
Mattegåta
En man har ett litet hål i väggen (lika stor som .problemly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.problemlly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px
.problemly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.problemlly38 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px  .problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 10px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;
.problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 10px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto; .problemly37 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px; height: 640px;
}
.problemlly37 {
padding: 5px 5px; border: 5px solid #526B7F;
.problemly37 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px; height: 640px;
}
.problemlly37 {
padding: 5px 5px; border: 5px solid #526B7F; .problem{
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #B2DCFF; -moz-border-radius: 10px; border-radius: 10px;
}
MattegåtaPå en gata finns två radhus och i varje radhus bor två djurgalna
.problem{
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #B2DCFF; -moz-border-radius: 10px; border-radius: 10px;
}
MattegåtaPå en gata finns två radhus och i varje radhus bor två djurgalna .problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 10px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;
.problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 10px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto; .sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;
margin-bottom: 10px; background: url(http://mattebloggen.com/wp-content/uploads/2010/09/satsbakgrund1.png) repeat; -moz-border-radius: 10px; border-radius: 10px; width:
.sats {
padding: 0px 5px; border: 3px solid #6f524a; margin: 0 auto;
margin-bottom: 10px; background: url(http://mattebloggen.com/wp-content/uploads/2010/09/satsbakgrund1.png) repeat; -moz-border-radius: 10px; border-radius: 10px; width: .problemly36 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px; height: 180px;
}
.problemlly36 {
padding: 5px 5px; border: 5px solid #526B7F;
.problemly36 {
padding: 5px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px; height: 180px;
}
.problemlly36 {
padding: 5px 5px; border: 5px solid #526B7F; Skolornas matematiktävling är den officiella mattetävlingen vi har för gymnasister i Sverige.
Förutom att att tävla i matte är jätteroligt, kan dina resultat också ge meritpoäng vid antagning på universitet/högskola, både som student och
Skolornas matematiktävling är den officiella mattetävlingen vi har för gymnasister i Sverige.
Förutom att att tävla i matte är jätteroligt, kan dina resultat också ge meritpoäng vid antagning på universitet/högskola, både som student och .problemy36 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #BBEE99; -moz-border-radius: 10px; border-radius: 10px;
}
MattegåtaEn springare hoppar alltid på schackbrädet antingen två rutor
.problemy36 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #BBEE99; -moz-border-radius: 10px; border-radius: 10px;
}
MattegåtaEn springare hoppar alltid på schackbrädet antingen två rutor .problemy351 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; height: 200px; -moz-border-radius: 10px; border-radius: 10px;
}
.problemy352 {
padding: 0px 5px; border: 5px solid #526B7F;
.problemy351 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; height: 200px; -moz-border-radius: 10px; border-radius: 10px;
}
.problemy352 {
padding: 0px 5px; border: 5px solid #526B7F; .problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
Mattegåta Hitta det största antalet kongruenta icke-konvexa polygoner som man
.problema34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
Mattegåta Hitta det största antalet kongruenta icke-konvexa polygoner som man .problemy36 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #BBEE99; -moz-border-radius: 10px; border-radius: 10px;
}
MattegåtaGissa vilken symbol som ska stå istället för frågetecknet i den
.problemy36 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: #BBEE99; -moz-border-radius: 10px; border-radius: 10px;
}
MattegåtaGissa vilken symbol som ska stå istället för frågetecknet i den .problemy34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
Mattegåta Hitta två äkta bråk, det ena med nämnaren 8 och det andra med
.problemy34 {
padding: 0px 5px; border: 5px solid #526B7F; margin: 0px 0 10px 0px; background-color: white; -moz-border-radius: 10px; border-radius: 10px;
}
Mattegåta Hitta två äkta bråk, det ena med nämnaren 8 och det andra med Mattegåta Cissi fyllde år så hon bakade en tårta till sin födelsedag. Tårtan var dock inte rund, utan formad som en regelbunden sexhörning ABCDEF. Cissi markerade K och L, som var mittpunkterna på sidorna EF och FA respektive. Sedan skar hon längs
Mattegåta Cissi fyllde år så hon bakade en tårta till sin födelsedag. Tårtan var dock inte rund, utan formad som en regelbunden sexhörning ABCDEF. Cissi markerade K och L, som var mittpunkterna på sidorna EF och FA respektive. Sedan skar hon längs  Snart är sommaren slut för min del och det är dags att sammanfatta vad jag lärt mig under mattekollotiden (jag var lärare för några av Rysslands mest skärpta åttor):
1. Åttan är lite för tidig årskurs för att introducera begreppet grupp.
2.
Snart är sommaren slut för min del och det är dags att sammanfatta vad jag lärt mig under mattekollotiden (jag var lärare för några av Rysslands mest skärpta åttor):
1. Åttan är lite för tidig årskurs för att introducera begreppet grupp.
2. Många har hört talas om den beryktade randvinkelsatsen. Eventuellt har du träffat på den på gymnasiet. Men få har egentligen koll på hur man bevisar satsen.
Om du vill komma fram till beviset själv med hjälp av några ledande uppgifter, se Cirklar
Många har hört talas om den beryktade randvinkelsatsen. Eventuellt har du träffat på den på gymnasiet. Men få har egentligen koll på hur man bevisar satsen.
Om du vill komma fram till beviset själv med hjälp av några ledande uppgifter, se Cirklar En tärning låg på bordet. Den flyttades ett steg i taget genom att rullas över på en ny sida (som gränsade till sidan som nyss var i kontakt med bordet). Till slut hamnade tärningen på samma plats som i början med samma sida uppåt. Kunde den översta
En tärning låg på bordet. Den flyttades ett steg i taget genom att rullas över på en ny sida (som gränsade till sidan som nyss var i kontakt med bordet). Till slut hamnade tärningen på samma plats som i början med samma sida uppåt. Kunde den översta  På dataskärmen står ett tal, som varje minut ökar med 102. Från början står det 123. Programmeraren Daniel kan när som helst ändra ordningen på siffrorna i talet på dataskärmen. Kan han garantera att talet aldrig blir
På dataskärmen står ett tal, som varje minut ökar med 102. Från början står det 123. Programmeraren Daniel kan när som helst ändra ordningen på siffrorna i talet på dataskärmen. Kan han garantera att talet aldrig blir På ett lager fanns likadana ostar. En natt kom sluga råttor dit och åt upp 10 av ostarna. Varje råtta åt lika mycket. Några råttor klarade dock inte av måltiden och fick ont i magen. Nästa natt kom de 7 råttorna som inte fick ont i magen och åt
På ett lager fanns likadana ostar. En natt kom sluga råttor dit och åt upp 10 av ostarna. Varje råtta åt lika mycket. Några råttor klarade dock inte av måltiden och fick ont i magen. Nästa natt kom de 7 råttorna som inte fick ont i magen och åt En fotboll är hopsydd av 32 lappar: vita sexkanter och svarta femkanter. Varje svart lapp gränsar till bara vita, varje vit lapp gränsar till tre vita och tre svarta lappar. Hur många vita lappar finns det i en
En fotboll är hopsydd av 32 lappar: vita sexkanter och svarta femkanter. Varje svart lapp gränsar till bara vita, varje vit lapp gränsar till tre vita och tre svarta lappar. Hur många vita lappar finns det i en På bordet ligger en papperscirkel med radien 5 cm. Så länge det är möjligt, lägger Ilian till papperskvadrater med sidan 5 cm intill cirkeln så att följande villkor uppfylls:
1. Varje kvadrat har ett hörn som nuddar cirkeln.
2. Kvadraterna
På bordet ligger en papperscirkel med radien 5 cm. Så länge det är möjligt, lägger Ilian till papperskvadrater med sidan 5 cm intill cirkeln så att följande villkor uppfylls:
1. Varje kvadrat har ett hörn som nuddar cirkeln.
2. Kvadraterna Härmed vill jag gratulera min mattecirkelelev, Benjamin Fayyazuddin-Ljungberg, för att han har blivit utvald till det svenska laget i tävlingsmatematik!
Tillsammans med 5 andra gymnasister kommer han att representera Sverige i den 51:a
Härmed vill jag gratulera min mattecirkelelev, Benjamin Fayyazuddin-Ljungberg, för att han har blivit utvald till det svenska laget i tävlingsmatematik!
Tillsammans med 5 andra gymnasister kommer han att representera Sverige i den 51:a På bordet ligger en papperscirkel med radien 5 cm. Så länge det är möjligt, lägger Ilian till papperskvadrater med sidan 5 cm intill cirkeln så att följande villkor uppfylls:
1. Varje kvadrat har ett hörn som nuddar cirkeln.
2. Kvadraterna
På bordet ligger en papperscirkel med radien 5 cm. Så länge det är möjligt, lägger Ilian till papperskvadrater med sidan 5 cm intill cirkeln så att följande villkor uppfylls:
1. Varje kvadrat har ett hörn som nuddar cirkeln.
2. Kvadraterna En och samma fredagsfilm startade samtidigt på två televisionskanaler. Ena kanalen delade upp filmen i stycken om 20 minuter och sände 2 minuter långa reklampauser mellan filmstycken. Den andra kanalen delade upp filmen i 10 minuters-stycken och
En och samma fredagsfilm startade samtidigt på två televisionskanaler. Ena kanalen delade upp filmen i stycken om 20 minuter och sände 2 minuter långa reklampauser mellan filmstycken. Den andra kanalen delade upp filmen i 10 minuters-stycken och På ett 10x10-bräde finns en pjäs i varje ruta. En tillåten operation är att välja en diagonal som innehåller ett jämnt antal pjäser och ta bort en valfri pjäs från den diagonalen. Hur många pjäser kan man som mest ta bort med hjälp av sådana
På ett 10x10-bräde finns en pjäs i varje ruta. En tillåten operation är att välja en diagonal som innehåller ett jämnt antal pjäser och ta bort en valfri pjäs från den diagonalen. Hur många pjäser kan man som mest ta bort med hjälp av sådana Thomas skrev ner alla dagar i en viss månad på en rad: 123456789101112... Sedan målade han över 3 av dagarna (som var hans kompisars födelsedagar) och inga övermålade dagar var precis efter varandra. Det visade sig att alla omålade områden består av
Thomas skrev ner alla dagar i en viss månad på en rad: 123456789101112... Sedan målade han över 3 av dagarna (som var hans kompisars födelsedagar) och inga övermålade dagar var precis efter varandra. Det visade sig att alla omålade områden består av  Eli och Tiffany är kompisar och bor i grannhus. Eli bor på nummer 4. Om Tiffany ska ta den kortaste vägen till Eli, så spelar det ingen roll på vilken sida hon springer runt hennes eget hus. Bestäm numret som Tiffany bor på.
Lösning:
Om
Eli och Tiffany är kompisar och bor i grannhus. Eli bor på nummer 4. Om Tiffany ska ta den kortaste vägen till Eli, så spelar det ingen roll på vilken sida hon springer runt hennes eget hus. Bestäm numret som Tiffany bor på.
Lösning:
Om Eli och Tiffany är kompisar och bor i grannhus. Eli bor på nummer 4. Om Tiffany ska ta den kortaste vägen till Eli, så spelar det ingen roll på vilken sida hon springer runt hennes eget hus. Bestäm numret som Tiffany bor
Eli och Tiffany är kompisar och bor i grannhus. Eli bor på nummer 4. Om Tiffany ska ta den kortaste vägen till Eli, så spelar det ingen roll på vilken sida hon springer runt hennes eget hus. Bestäm numret som Tiffany bor Rekommenderad från: 12 år
[kkratings]
Eli bor i ett höghus med 9 våningar. Han kan åka hiss från sin egen våning till den första och då tar det 1 minut.
Men han når inte knappen till sin egen våning, eftersom han är så liten. Istället trycker
Rekommenderad från: 12 år
[kkratings]
Eli bor i ett höghus med 9 våningar. Han kan åka hiss från sin egen våning till den första och då tar det 1 minut.
Men han når inte knappen till sin egen våning, eftersom han är så liten. Istället trycker  Rekommenderad från: 13 år
[kkratings]
Du har hittat en skatt som består av 6 stycken antika mynt. I skattkistan låg en lapp som berättade om att ett av mynten är falskt. Det väger inte lika mycket som de riktiga mynten (de riktiga mynten väger
Rekommenderad från: 13 år
[kkratings]
Du har hittat en skatt som består av 6 stycken antika mynt. I skattkistan låg en lapp som berättade om att ett av mynten är falskt. Det väger inte lika mycket som de riktiga mynten (de riktiga mynten väger  Det här är fortsättningen på inlägget Transformationsmatrisen - del 1. I första delen behandlas begreppet baser.
Vektorer i olika baser
Vektorer som skrivs med hjälp av siffror till exempel så här $$\left(\begin{array}{c}
\sqrt{2}
Det här är fortsättningen på inlägget Transformationsmatrisen - del 1. I första delen behandlas begreppet baser.
Vektorer i olika baser
Vektorer som skrivs med hjälp av siffror till exempel så här $$\left(\begin{array}{c}
\sqrt{2} De flesta matematik- och ingenjörsstudenter läser någon form av linjär algebra. Det är ett högst rimlig inslag i deras utbildning - vilken vuxen människa räknar inte med matriser :)?
Just beräkningar är dessutom det studenterna måste lära sig
De flesta matematik- och ingenjörsstudenter läser någon form av linjär algebra. Det är ett högst rimlig inslag i deras utbildning - vilken vuxen människa räknar inte med matriser :)?
Just beräkningar är dessutom det studenterna måste lära sig Rekommenderad från: 11 år
[kkratings]
Pelle delade upp ett 8x8-bräde i 30 stycken rektanglar på så sätt att likadana rektanglar inte nuddar varandra, inte ens med hörn. Försök att förbättra hans resultat genom att dela upp brädet i ännu
Rekommenderad från: 11 år
[kkratings]
Pelle delade upp ett 8x8-bräde i 30 stycken rektanglar på så sätt att likadana rektanglar inte nuddar varandra, inte ens med hörn. Försök att förbättra hans resultat genom att dela upp brädet i ännu Rekommenderad från: 15 år
[kkratings]
Mattebloggen har en inofficiell tävling i att lösa matematikproblem. Skicka in din lösning med motivering till valentina.chapovalova@gmail.com, så har du chansen att vara med på topplistan. Har du någon
Rekommenderad från: 15 år
[kkratings]
Mattebloggen har en inofficiell tävling i att lösa matematikproblem. Skicka in din lösning med motivering till valentina.chapovalova@gmail.com, så har du chansen att vara med på topplistan. Har du någon Rekommenderad från: 12 år
[kkratings]
Kan man dela upp en kvadrat i 9 kvadrater och måla en av dem i vitt, 3 av dem i grått och 5 av dem i svart på så sätt att kvadrater med samma färg har samma storlek, men kvadrater med olika färg har
Rekommenderad från: 12 år
[kkratings]
Kan man dela upp en kvadrat i 9 kvadrater och måla en av dem i vitt, 3 av dem i grått och 5 av dem i svart på så sätt att kvadrater med samma färg har samma storlek, men kvadrater med olika färg har Under höstterminen kom gåtorna varje vecka och den som löster allra flest var Johan B. Här ser ni honom tillsammans med första priset:
Vinnaren bland studenter var Erik R. och bland högstadieelever var det Olle K., Hanna H., Jennifer U.-L.,
Under höstterminen kom gåtorna varje vecka och den som löster allra flest var Johan B. Här ser ni honom tillsammans med första priset:
Vinnaren bland studenter var Erik R. och bland högstadieelever var det Olle K., Hanna H., Jennifer U.-L., Rekommenderad från: 14 år
[kkratings]
Det finns en platt kvadratisk tavla som är 1 dm x 1 dm stor. Vi säger att ett pappersark i form av en rektangel med area 2 dm2 är ett omslag om man kan slå in tavlan i pappret så att båda sidorna
Rekommenderad från: 14 år
[kkratings]
Det finns en platt kvadratisk tavla som är 1 dm x 1 dm stor. Vi säger att ett pappersark i form av en rektangel med area 2 dm2 är ett omslag om man kan slå in tavlan i pappret så att båda sidorna  Rekommenderad från: 11 år
[kkratings]
Aladdin vill sätta Jafar i ett fängelse som består av 4 rum och 3 smala gångar mellan rummen. I varje gång står en tjock och trött vakt lutandes mot en av väggarna. Varje gång Jafar går över
Rekommenderad från: 11 år
[kkratings]
Aladdin vill sätta Jafar i ett fängelse som består av 4 rum och 3 smala gångar mellan rummen. I varje gång står en tjock och trött vakt lutandes mot en av väggarna. Varje gång Jafar går över Rekommenderad från: 12 år
[kkratings]
Benny skrev upp namnet på sin hemstad och alla cykliska "förskjutningar" av det och fick tabell 1. Sedan ordnade han om namnen och skrev de i bokstavsordning i tabell 2 i
Rekommenderad från: 12 år
[kkratings]
Benny skrev upp namnet på sin hemstad och alla cykliska "förskjutningar" av det och fick tabell 1. Sedan ordnade han om namnen och skrev de i bokstavsordning i tabell 2 i Rekommenderad från: 12 år
[kkratings]
En sifferkod, som består av 7 olika siffror kallas för godkänd sifferkod. Man vet att ett kassaskåp har en viss okänd godkänd sifferkod.
Om man slår in någon godkänd kod och åtminstone en rätt
Rekommenderad från: 12 år
[kkratings]
En sifferkod, som består av 7 olika siffror kallas för godkänd sifferkod. Man vet att ett kassaskåp har en viss okänd godkänd sifferkod.
Om man slår in någon godkänd kod och åtminstone en rätt Rekommenderad från: 10 år
[kkratings]
Dela upp figuren på bilden i två sammanhängande delar, på så sätt att det går att sätta ihop delarna till en kvadrat 8*8.
Visa lösningen
Så här kan man
Rekommenderad från: 10 år
[kkratings]
Dela upp figuren på bilden i två sammanhängande delar, på så sätt att det går att sätta ihop delarna till en kvadrat 8*8.
Visa lösningen
Så här kan man Rekommenderad från: 14 år
[kkratings]
Fredrik står i mitten av en rund gräsmatta, som har radien 100 meter. Varje steg Fredrik tar är 1 meter långt. Varje gång han ska ta ett nytt steg anger han riktningen som han ska gå i. Anna har
Rekommenderad från: 14 år
[kkratings]
Fredrik står i mitten av en rund gräsmatta, som har radien 100 meter. Varje steg Fredrik tar är 1 meter långt. Varje gång han ska ta ett nytt steg anger han riktningen som han ska gå i. Anna har Rekommenderad från: 12 år
[kkratings]
I en stad finns 6 torg. Ur varje torg utgår 3 raka vägar till exakt 3 andra torg. Inga två vägar korsar varandra. Bland de tre vägarna, som utgår från samma torg, ligger ena vägen inuti vinkeln,
Rekommenderad från: 12 år
[kkratings]
I en stad finns 6 torg. Ur varje torg utgår 3 raka vägar till exakt 3 andra torg. Inga två vägar korsar varandra. Bland de tre vägarna, som utgår från samma torg, ligger ena vägen inuti vinkeln, Rekommenderad från: 14 år
[kkratings]
Det finns ett rutigt papper. På det finns rektanglar som har sin gräns gående längs med rutorna. Varje rektangel består av ett udda antal rutor och inga två rektanglar har gemensamma inre rutor.
Rekommenderad från: 14 år
[kkratings]
Det finns ett rutigt papper. På det finns rektanglar som har sin gräns gående längs med rutorna. Varje rektangel består av ett udda antal rutor och inga två rektanglar har gemensamma inre rutor. Rekommenderad från: 11 år
[kkratings]
Cissi klippte ut två likadana figurer ur en stor kartong. Sedan la hon dem på bottnen av en rektangulär låda så att de delvis täckte varandra. Det visade sig att hela bottnen blev täckt.
Sedan slog Kalle in en
Rekommenderad från: 11 år
[kkratings]
Cissi klippte ut två likadana figurer ur en stor kartong. Sedan la hon dem på bottnen av en rektangulär låda så att de delvis täckte varandra. Det visade sig att hela bottnen blev täckt.
Sedan slog Kalle in en  Rekommenderad från: 13 år
[kkratings]
Vargen bjöd hem de tre små grisarna och Rödluvan för att titta på film. Efter att de var klara gick Vargen till köket, räknade alla kex och upptäckte att det saknades två. Men han har en stor
Rekommenderad från: 13 år
[kkratings]
Vargen bjöd hem de tre små grisarna och Rödluvan för att titta på film. Efter att de var klara gick Vargen till köket, räknade alla kex och upptäckte att det saknades två. Men han har en stor Rekommenderad från: 10 år
[kkratings]
Rita sex streck, så att alla 16 punkter på bilden blir överstrukna, utan att lyfta pennan från pappret och utan att strecken går längs med rutnätet.
Visa lösningen
Så här till
Rekommenderad från: 10 år
[kkratings]
Rita sex streck, så att alla 16 punkter på bilden blir överstrukna, utan att lyfta pennan från pappret och utan att strecken går längs med rutnätet.
Visa lösningen
Så här till Första träffen på höstens mattecirkel äger rum på onsdagen den 2:a september kl. 15.20 i sal 169 på Katedralskolan i Uppsala. Alla nyfikna är välkomna! Det enda man behöver ha med sig är penna och
Första träffen på höstens mattecirkel äger rum på onsdagen den 2:a september kl. 15.20 i sal 169 på Katedralskolan i Uppsala. Alla nyfikna är välkomna! Det enda man behöver ha med sig är penna och Jag är glad att annonsera nyheten: det kommer hållas en matematikcirkel för intresserade gymnasieelever i höst! Som bas kommer jag att ha Katedralskolan i Uppsala (alternativt rektorsvillan), men elever från alla skolor är givetvis välkomna.
Detta
Jag är glad att annonsera nyheten: det kommer hållas en matematikcirkel för intresserade gymnasieelever i höst! Som bas kommer jag att ha Katedralskolan i Uppsala (alternativt rektorsvillan), men elever från alla skolor är givetvis välkomna.
Detta Ännu en juli har passerat då jag har jobbat som lärare på ett mattekollo. Det var en spännande månad med tonvis jobb och upplevelser.
Vi organiserade
Ännu en juli har passerat då jag har jobbat som lärare på ett mattekollo. Det var en spännande månad med tonvis jobb och upplevelser.
Vi organiserade Rekommenderad från: 15 år
[kkratings]
Låt F1 vara en godtycklig konvex fyrhörning. För k>1, Fk konstrueras genom att man skär Fk-1 i två delar längs en av dess diagonaler, vänder på en av delarna och sedan klistrar delarna samman längs
Rekommenderad från: 15 år
[kkratings]
Låt F1 vara en godtycklig konvex fyrhörning. För k>1, Fk konstrueras genom att man skär Fk-1 i två delar längs en av dess diagonaler, vänder på en av delarna och sedan klistrar delarna samman längs  Rekommenderad från: 15 år
[kkratings]
Tag en vanlig kortlek med 52 kort. Säg att kortleken ligger snyggt, ifall varje par av kort där ena ligger på den andra antingen har samma färg eller samma valör, samma sak gäller för det översta
Rekommenderad från: 15 år
[kkratings]
Tag en vanlig kortlek med 52 kort. Säg att kortleken ligger snyggt, ifall varje par av kort där ena ligger på den andra antingen har samma färg eller samma valör, samma sak gäller för det översta  Rekommenderad från: 13 år
[kkratings]
Vi människor läser vanligtvis från vänster till höger och uppifrån och ner. Ödlor är inte lika snabba på att läsa, men de kan göra det på fler olika sätt. Ödlan kan läsa en bokstav och sedan
Rekommenderad från: 13 år
[kkratings]
Vi människor läser vanligtvis från vänster till höger och uppifrån och ner. Ödlor är inte lika snabba på att läsa, men de kan göra det på fler olika sätt. Ödlan kan läsa en bokstav och sedan Rekommenderad från: 15 år
[kkratings]
Det finns en rutig remsa 1xn:
Anders och Filip spelar ett spel. De turas om att göra drag: Anders får sätta ett kryss i en tom ruta och Filip får sätta en ring i en tom ruta. Dock får inte två
Rekommenderad från: 15 år
[kkratings]
Det finns en rutig remsa 1xn:
Anders och Filip spelar ett spel. De turas om att göra drag: Anders får sätta ett kryss i en tom ruta och Filip får sätta en ring i en tom ruta. Dock får inte två  Rekommenderad från: 13 år
[kkratings]
55 indier och turkar träffades på ett tehus. Varje person drack antingen te eller kaffe. När en indier dricker te så talar hen alltid sanning och när hen dricker kaffe så luras hen alltid, medan
Rekommenderad från: 13 år
[kkratings]
55 indier och turkar träffades på ett tehus. Varje person drack antingen te eller kaffe. När en indier dricker te så talar hen alltid sanning och när hen dricker kaffe så luras hen alltid, medan Rekommenderad från: 12 år
[kkratings]
En trollkarl med förbundna ögon och hans assistent utför följande trick. Trollkarlen har 29 kort med talen 1 till 29 på. Han ger korten till någon person i publiken, som väljer ut två av dem.
Rekommenderad från: 12 år
[kkratings]
En trollkarl med förbundna ögon och hans assistent utför följande trick. Trollkarlen har 29 kort med talen 1 till 29 på. Han ger korten till någon person i publiken, som väljer ut två av dem. Rekommenderad från: 10 år
[kkratings]
På ett papper finns en bild på en svart kvadrat. Du har tillgång till 7 kvadratformade brickor av samma storlek som den ritade kvadraten. Hur ska du göra för att täcka över kvadraten med
Rekommenderad från: 10 år
[kkratings]
På ett papper finns en bild på en svart kvadrat. Du har tillgång till 7 kvadratformade brickor av samma storlek som den ritade kvadraten. Hur ska du göra för att täcka över kvadraten med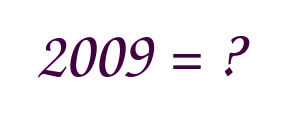 Rekommenderad från: 15 år
[kkratings]
På hur många sätt kan man skriva talet 2009 som en summa av några positiva nästan lika heltal? Talen kallas nästa lika om deras skillnad är (till beloppet) maximalt 1. Sätten betraktas som samma om
Rekommenderad från: 15 år
[kkratings]
På hur många sätt kan man skriva talet 2009 som en summa av några positiva nästan lika heltal? Talen kallas nästa lika om deras skillnad är (till beloppet) maximalt 1. Sätten betraktas som samma om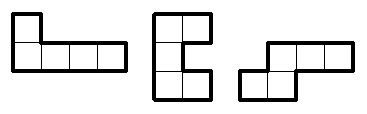 Rekommenderad från: 10 år
Förkunskaper: spegelsymmetri
[kkratings]
Bygg ihop bitarna nedan till en spegelsymmetrisk figur. Varje bit skall användas exakt en gång.
Visa lösningen
Det finns åtminstone tre
Rekommenderad från: 10 år
Förkunskaper: spegelsymmetri
[kkratings]
Bygg ihop bitarna nedan till en spegelsymmetrisk figur. Varje bit skall användas exakt en gång.
Visa lösningen
Det finns åtminstone tre Om du precis har börjat intressera dig för matematik, då säger jag grattis! Du kommer att bli fascinerad av problem, teorier och bevis många gånger!
Det är inte lika lätt om man fått matematiken serverad på ett guldfat sedan barnsben (eller
Om du precis har börjat intressera dig för matematik, då säger jag grattis! Du kommer att bli fascinerad av problem, teorier och bevis många gånger!
Det är inte lika lätt om man fått matematiken serverad på ett guldfat sedan barnsben (eller Rekommenderad från: 12 år
[kkratings]
På ett område 1km x 1km växer en tallskog. Alla tallarna har diametern 50 cm. Visa att en fältbiolog kan hitta en ledig rektangel 10m x 20m i skogen, för att kunna sola där med alla sina vänner om
Rekommenderad från: 12 år
[kkratings]
På ett område 1km x 1km växer en tallskog. Alla tallarna har diametern 50 cm. Visa att en fältbiolog kan hitta en ledig rektangel 10m x 20m i skogen, för att kunna sola där med alla sina vänner om Rekommenderad från: 12 år
[kkratings]
En balansvåg har två skålar. Om tyngderna på skålarna är lika visar balansvågen jämvikt. Annars visar den vilken skål som är tyngre.
Det finns en stor påse strösocker, en balansvåg samt en
Rekommenderad från: 12 år
[kkratings]
En balansvåg har två skålar. Om tyngderna på skålarna är lika visar balansvågen jämvikt. Annars visar den vilken skål som är tyngre.
Det finns en stor påse strösocker, en balansvåg samt en Här är ett smakprov av vår andra lektion, som handlar om att väga saker på en balansvåg och avgöra om de är lätta, tunga, falska etc. Här nedan ser ni några av lektionens svåraste problem.
Nu kan man försöka analysera vad det är egentligen som
Här är ett smakprov av vår andra lektion, som handlar om att väga saker på en balansvåg och avgöra om de är lätta, tunga, falska etc. Här nedan ser ni några av lektionens svåraste problem.
Nu kan man försöka analysera vad det är egentligen som  Eller en ekvivalent fråga: kan man lära sig matte med hjälp av spel?
Jag har lagt till en spelsida på bloggen med lite snodda småpussel. Syftet med detta är ännu oklart, men det fick mig att tänka på ovanstående frågor. Så nu menar jag alltså spel
Eller en ekvivalent fråga: kan man lära sig matte med hjälp av spel?
Jag har lagt till en spelsida på bloggen med lite snodda småpussel. Syftet med detta är ännu oklart, men det fick mig att tänka på ovanstående frågor. Så nu menar jag alltså spel Rekommenderad från: 15 år
[kkratings]
En dag bestämde sig en snigel för att starta en resa. Snigeln rörde sig framåt längs med en rak sträcka i 6 minuter tills det var nog för dagen. Under den tiden kom några människor och tittade på
Rekommenderad från: 15 år
[kkratings]
En dag bestämde sig en snigel för att starta en resa. Snigeln rörde sig framåt längs med en rak sträcka i 6 minuter tills det var nog för dagen. Under den tiden kom några människor och tittade på  Rekommenderad från: 12 år
[kkratings]
En lägenhet består av ett antal rum som kan ha olika areor. Det går att dela lägenheten mellan 2, 3 eller 4 hyresgäster så att varje person får bo på samma area (fast antalet rum kan vara olika).
Rekommenderad från: 12 år
[kkratings]
En lägenhet består av ett antal rum som kan ha olika areor. Det går att dela lägenheten mellan 2, 3 eller 4 hyresgäster så att varje person får bo på samma area (fast antalet rum kan vara olika). Jag har precis börjat mattecirkeln med Anna, en elev som nu går i nian i Uppsala.
Det är många som frågat mig vad "mattecirkel" egentligen betyder, för det känns kanske lite dumt att kalla någonting för "cirkel" när bara två personer träffas. Men
Jag har precis börjat mattecirkeln med Anna, en elev som nu går i nian i Uppsala.
Det är många som frågat mig vad "mattecirkel" egentligen betyder, för det känns kanske lite dumt att kalla någonting för "cirkel" när bara två personer träffas. Men Jag ska försöka reda ut begreppet linjär avbildning. Det är trots allt det linjär algebra i stort sett handlar om.
För det första är linjär avbildning synonymt begrepp med linjär transformation, och båda varianterna används flitigt. Detta tyder på
Jag ska försöka reda ut begreppet linjär avbildning. Det är trots allt det linjär algebra i stort sett handlar om.
För det första är linjär avbildning synonymt begrepp med linjär transformation, och båda varianterna används flitigt. Detta tyder på Rekommenderad från: 12 år
[kkratings]
Rita två fyrkanter, som tillsammans kan läggas ihop till
(i) En triangel, men också en femkant
(ii) Både en triangel, en fyrkant och en femkant.
Med "läggas ihop" menas att fyrkanterna inte
Rekommenderad från: 12 år
[kkratings]
Rita två fyrkanter, som tillsammans kan läggas ihop till
(i) En triangel, men också en femkant
(ii) Både en triangel, en fyrkant och en femkant.
Med "läggas ihop" menas att fyrkanterna inte Rekommenderad från: 12 år
I havet bor många olika bläckfiskar. Om en bläckfisk har ett jämnt antal armar så talar den alltid sanning, men om den har udda anta armar så ljuger den alltid. En gång sade den gröna bläckfisken till den
Rekommenderad från: 12 år
I havet bor många olika bläckfiskar. Om en bläckfisk har ett jämnt antal armar så talar den alltid sanning, men om den har udda anta armar så ljuger den alltid. En gång sade den gröna bläckfisken till den Rekommenderad från: 15 år
Från början har vi en kvartscirkel med radie 1 cm. Gränserna för kvartscirkeln utgör diametrar för två mindre cirklar, deras halvor syns på bilden.
i) Hur förhåller sig areorna A och B?
ii) Vad
Rekommenderad från: 15 år
Från början har vi en kvartscirkel med radie 1 cm. Gränserna för kvartscirkeln utgör diametrar för två mindre cirklar, deras halvor syns på bilden.
i) Hur förhåller sig areorna A och B?
ii) Vad Rekommenderad från: 12 år
Visa att en kvadrat kan delas upp i n stycken mindre kvadrater för alla n>5. Med "att dela upp" menas att vi klipper en kvadrat så att alla erhållna delar också är kvadrater och det blir inga bitar över.
Rekommenderad från: 12 år
Visa att en kvadrat kan delas upp i n stycken mindre kvadrater för alla n>5. Med "att dela upp" menas att vi klipper en kvadrat så att alla erhållna delar också är kvadrater och det blir inga bitar över. Rekommenderad från: 10 år
Dela upp hjärtfiguren nedan i 8 likadana delar. Delarna räknas som likadana om de har samma form och storlek (de kan dock vara placerade på olika sätt).
Visa lösningen
Första lösningen kommer från min
Rekommenderad från: 10 år
Dela upp hjärtfiguren nedan i 8 likadana delar. Delarna räknas som likadana om de har samma form och storlek (de kan dock vara placerade på olika sätt).
Visa lösningen
Första lösningen kommer från min  Från Wikipedia: Låt P(n) vara ett påstående som har att göra med ett positivt heltal n, och antag att följande påståenden är sanna:
P(1) är sant.
.
Då är påståendet P(n) sant för varje val av det positiva heltalet n.
Lätt som en plätt,
Från Wikipedia: Låt P(n) vara ett påstående som har att göra med ett positivt heltal n, och antag att följande påståenden är sanna:
P(1) är sant.
.
Då är påståendet P(n) sant för varje val av det positiva heltalet n.
Lätt som en plätt, Rekommenderad från: 15 år
Förkunskaper: intervall, tallinjen, delbarhet, potenser.
På reella tallinjen markerade Johan alla kvadrater på positiva heltal. Varje erhållet intervall delade han sedan i två lika stora delar, de vänstra
Rekommenderad från: 15 år
Förkunskaper: intervall, tallinjen, delbarhet, potenser.
På reella tallinjen markerade Johan alla kvadrater på positiva heltal. Varje erhållet intervall delade han sedan i två lika stora delar, de vänstra Rekommenderad från: 10 år
[kkratings]
I staden Bilköping finns en parkering med plats för 7x7 bilar. Man kan komma in endast genom porten, resten av parkeringsplatsen är omsluten med staket. En vakt vill parkera så många bilar som
Rekommenderad från: 10 år
[kkratings]
I staden Bilköping finns en parkering med plats för 7x7 bilar. Man kan komma in endast genom porten, resten av parkeringsplatsen är omsluten med staket. En vakt vill parkera så många bilar som Lektionerna nummer ett är nu avklarade!
Det är alltid lite mer nervöst att ha lektion i en ny kurs för första gången, än med en ny grupp, men nu hände båda sakerna på en gång. Sedan var det en ny grupp tre gången till :). Varje gång gick jag
Lektionerna nummer ett är nu avklarade!
Det är alltid lite mer nervöst att ha lektion i en ny kurs för första gången, än med en ny grupp, men nu hände båda sakerna på en gång. Sedan var det en ny grupp tre gången till :). Varje gång gick jag
2+3=10 7+2=63 6+5=66 8+4=96 8+7=????
144
120
144 är rätt
Med den information som ges är 120 inte en felaktig slutsats.
Med informationen som ges, hur kan det bli 144?
Det borde bli 120, för varje tal som skrivet är summan multiplicerat med det första talet. Det sista borde alltså bli 15*8 = 120..
Hur många kanter har en cirkel
Hur många kanter har en cirkel
Hur går det med årets tävling?
Den nya tävlingen börjar nästa vecka på tisdag! Jag har filat på ett nytt svarssystem och det är nästan klart.
Har inte du fått in min lösning på 9.3?
Jo, det har jag fått. Jag har bara inte rättat den än.
Tävlingsdeltagare!
Ni är så duktiga på att skicka in lösningar, att jag inte alltid hinner med alla på en gång :)
Så det kan ta några dagar innan jag svarar er med problemresultat.
För övrigt, som det ser ut ska det gå att skicka in lösningar på de två senaste problemuppsättningar.
vet någon denna 2 söner och 2 fäder åt en pepparkaka var tillsammans åt dom 3 pepparkaker
Yes, en klassiker! :) Vet du svaret eller vill du ha tips?
kan du ändra om talen i figuren så att alla sidor får summan 20
En kub har sidan 2, tre genomgående hål med radien 1 borras rakt igenom längs x, y och z-axlarna. Origo är i centrum på kuben och hålen går ut vinkelrätt ur kubens sidor. 8 st volymsobjekt blir då kvar. I verkligheten skulle faktiskt kubben falla isär i dessa 8 bitar efter att man borrat det tredje hålet. Bestäm deras volym. Har någon en enkel lösning på detta, jag har en rätt komplicerad variant