På reella tallinjen markerade Johan alla kvadrater på positiva heltal. Varje erhållet intervall delade han sedan i två lika stora delar, de vänstra halvorna målade han blått (inklusive vänstra änden), medan de högra målade han rött (exklusive högra änden).
1. Visa att för varje positivt heltal n kan han hitta ett blått tal som är delbart med talet n.
2. Visa att för varje positivt heltal n kan han hitta ett rött tal som är delbart med talet n.
3. Visa att Johan kan hitta 1000 olika positiva heltal, så att summan av vilka som helst 5 av dem är ett rött tal.
4. Visa att det finns oändligt många röda tal som är potenser av två.
1. Varje tal 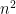 är ju blått, kvadraterna är alltid de vänstra ändarna av intervallen. Och
är ju blått, kvadraterna är alltid de vänstra ändarna av intervallen. Och 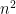 är delbart med
är delbart med  .
.
2. Varje tal  är däremot rött. Även
är däremot rött. Även  är rött.
är rött. 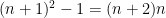 som då är delbart med
som då är delbart med  .
.
3. Vi ser att längderna på röda intervall ökar med tiden. Först är det 1,5, sedan 2,5 sedan 3,5 och så vidare. Det beror på att skillnaden mellan två på varandra följande kvadrater är ett udda tal och alla udda tal förekommer på det sättet.  . Huvudsaken är i vilket fall att röda intervall ökar till längden. Hitta ett jättestort rött intervall. Hitta sedan det första talet i det, som kan skrivas som
. Huvudsaken är i vilket fall att röda intervall ökar till längden. Hitta ett jättestort rött intervall. Hitta sedan det första talet i det, som kan skrivas som  (alla stora tal delbara med 5 kan skrivas så). Det uttrycket är nämligen summan utav
(alla stora tal delbara med 5 kan skrivas så). Det uttrycket är nämligen summan utav  och
och  .
.
Som våra tusen tal tar vi då  . Vilka fem av dem vi än tar kommer deras summa vara större än eller lika med
. Vilka fem av dem vi än tar kommer deras summa vara större än eller lika med  och mindre än eller lika med
och mindre än eller lika med  . Väljer vi längden på det röda intervallet lika med 5000,5 så är vi säkra på att den största summan är röd.
. Väljer vi längden på det röda intervallet lika med 5000,5 så är vi säkra på att den största summan är röd.
Notera att vi här inte behövde lista just vilka tal vi valde. Det räcker att visa att det går, precis vad det frågas efter i uppgiften.
4. (Obs! Formlerna har försvunnit. Försök att fylla i själv :)) Vilka potenser av 2 kan vara röda? Inte de jämna i alla fall, för att [], det vill säga jämna tvåpotenser är kvadrat på naturliga tal, och alla kvadrater är ju blå. De enda vi kan hoppas på är udda potenser, []. För att de ska hamna i röda intervall måste de vara i den högra halvan av intervallet mellan [] och [] för något naturligt tal n.
Vänstra begränsningen är alltså mittpunkten på intervallet, som är [] och högra är []. Således måste []. Alla talen är positiva, alltså kan vi dra roten ur varje led. Notera att roten ur [] är mindre än [], så alla k som uppfyller [] är också k som passar oss. [] ska alltså befinna sig mellan två på varandra följande heltal och dess bråktalsdel (talet minus heltalsdelen) skall vara större än [].
Vi börjar alltså med [] och multiplicerar den med två k gånger. Vi ska bevisa att talen aldrig kommer fastna med bråkdelen mindre än eller lika med []. Notera att eftersom [] är ett irrationellt tal, så kommer vi aldrig att komma fram till ett heltal genom att dubbla, det vill säga bråktalsdelen kommer aldrig att bli 0. Antag att den någon gång blir mellan 0 och []. Då kommer den efter några dubbleringar att bli mellan [] och 1, eftersom den ökar hela tiden, och den kan inte ”hoppa över” de decimalerna vi vill åt: någonting, som är mindre än [], gånger 2 blir någonting, som är mindre 1. Därför kommer vi alltid att komma tillbaka till bra bråktalsdel. Vi har hittat oändligt många k som passar, och således också oändligt många (udda) tvåpotenser!

