En trollkarl med förbundna ögon och hans assistent utför följande trick. Trollkarlen har 29 kort med talen 1 till 29 på. Han ger korten till någon person i publiken, som väljer ut två av dem. Resten av korten ges till assistenten, som sedan väljer två av de resterande korten och visar till personen i publiken. Personen läser upp högt båda talen för trollkarlen (i vilken ordning han vill). Därefter gissar trollkarlen vilka kort som personen valde ut i början.
Hur skall trollkarlen och assistenen förbereda sig för att alltid lyckas med tricket?
Diskussion:
Problemet kan först verka svårt när vi har så många kort att hålla reda på. När talet i uppgiften är stort, försök att lösa samma uppgift, fast med ett mindre tal. Välj till exempel antalet kort till 5.
Ifall bara 4 kort är inblandade handlar det inte om något trick längre. Assistenen kan ju bara välja de två korten som är kvar och trollkarlen gissar förstås vilka kort som saknas.
Lösning för 5 kort:
För att tricket alltid ska funka måste varje par av tal som trollkarlen hör ge ett bestämt par av tal som trollkarlen sedan ska gissa på. Det gäller alltså att ”para ihop” par av tal och alla dessa fyra tal måste vara olika för lyckat trick. För 5 tal kanske man listar ut svaren på följande sätt:
Para ihop alla kanter i en femhörning med var sin diagonal så som det ser ut på bilden. 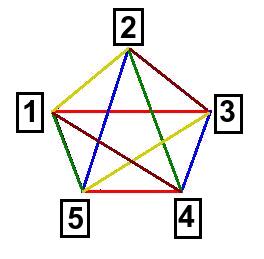
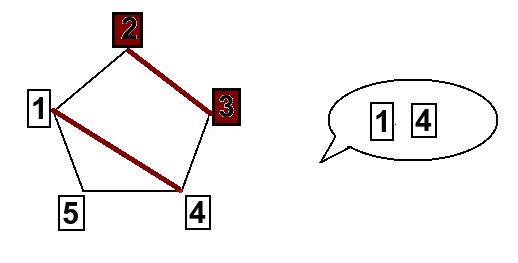 Till exempel så är följande kanter bruna: den som binder ihop 2 & 3, samt den som binder ihop 1 & 4. Ifall assistenten ser att åskådaren plockar bort korten 2 och 3, så pekar han på korten 1 & 4 och trollkarlen kan då komma ihåg att kanten 1 & 4 hade den bruna färgen och säga exakt vilka kort som plockades bort från början (de som också hade den bruna färgen).
Till exempel så är följande kanter bruna: den som binder ihop 2 & 3, samt den som binder ihop 1 & 4. Ifall assistenten ser att åskådaren plockar bort korten 2 och 3, så pekar han på korten 1 & 4 och trollkarlen kan då komma ihåg att kanten 1 & 4 hade den bruna färgen och säga exakt vilka kort som plockades bort från början (de som också hade den bruna färgen).
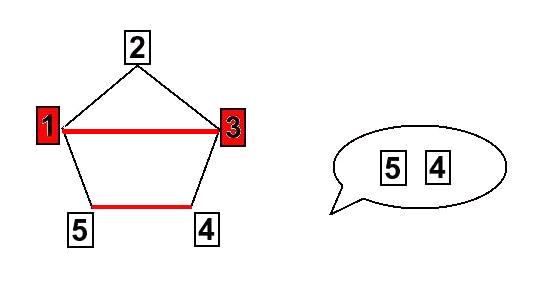
Ett annat exempel vore om personen i publiken valde korten 1 & 3, så pekar assistenten på korten 4 & 5 eftersom de paren har samma röda färg:
Lösning för 29 kort:
De flesta skickade in lösningen som följer. Här gäller det att tänka som att alla korten läggs på rad och att efter 29 kommer 1 igen. Trollkarlen och assistenten kan även tänka att korten ligger i en cirkel i ordning.
Vad händer då om en person i publiken väljer vilka som helst två kort? Om de inte ligger bredvid varandra, så pekar assistenten på de korten som ligger direkt efter vart och ett av de bortplockade, som till exempel här:
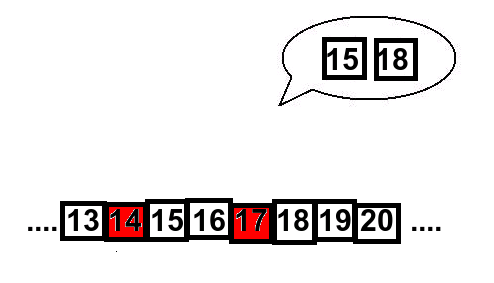 Om de valda korten ligger bredvid varandra, så pekar assistenen på två kort som också ligger bredvid varandra, nämnligen de två som kommer direkt efter. Här är ett exempel:
Om de valda korten ligger bredvid varandra, så pekar assistenen på två kort som också ligger bredvid varandra, nämnligen de två som kommer direkt efter. Här är ett exempel:
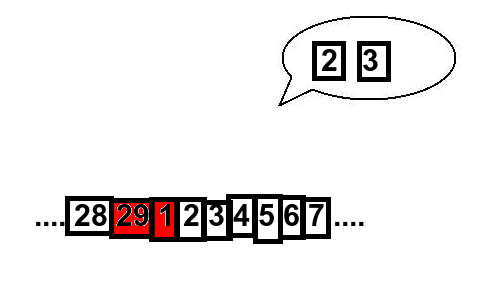
Trollkarlen kan se skillnad på de olika fallen. Ligger de talen han hör inte bredvid varandra, så gäller det första fallet. Då ska han bara subtrahera 1 från varje (och säga 29 ifall något av talen var 1). Ligger talen bredvid varandra, så ska han subtrahera 2 från varje (på samma sätt här, lite speciell subtraktion vid gränsen).
Notera att lösningen fungerar på samma sätt för vilket som helst antal kort och inte bara 29.



 Till exempel så är följande kanter bruna: den som binder ihop 2 & 3, samt den som binder ihop 1 & 4. Ifall assistenten ser att åskådaren plockar bort korten 2 och 3, så pekar han på korten 1 & 4 och trollkarlen kan då komma ihåg att kanten 1 & 4 hade den bruna färgen och säga exakt vilka kort som plockades bort från början (de som också hade den bruna färgen).
Till exempel så är följande kanter bruna: den som binder ihop 2 & 3, samt den som binder ihop 1 & 4. Ifall assistenten ser att åskådaren plockar bort korten 2 och 3, så pekar han på korten 1 & 4 och trollkarlen kan då komma ihåg att kanten 1 & 4 hade den bruna färgen och säga exakt vilka kort som plockades bort från början (de som också hade den bruna färgen).
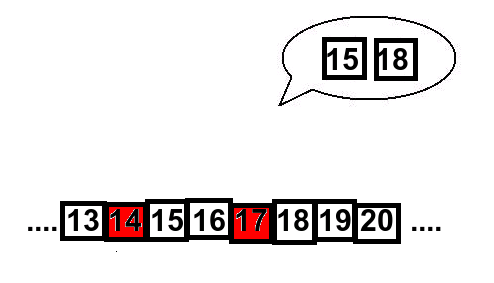 Om de valda korten ligger bredvid varandra, så pekar assistenen på två kort som också ligger bredvid varandra, nämnligen de två som kommer direkt efter. Här är ett exempel:
Om de valda korten ligger bredvid varandra, så pekar assistenen på två kort som också ligger bredvid varandra, nämnligen de två som kommer direkt efter. Här är ett exempel: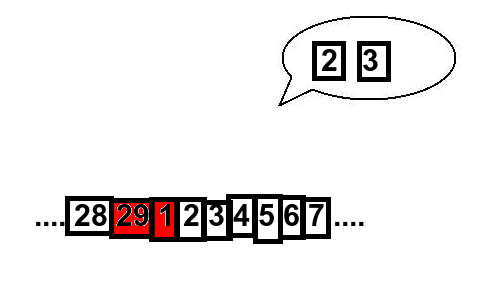
För en lite enklare version av problemet, ersätt 29 med 5. Det vill säga förklara tricket med 5 kort.