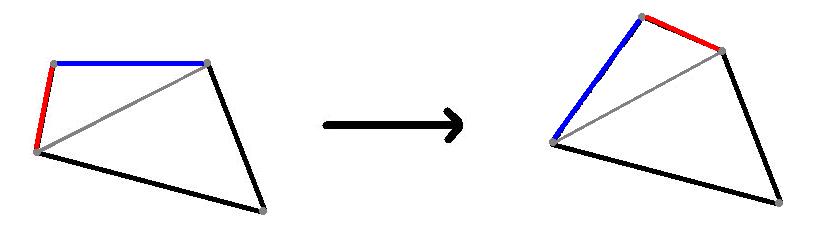
Notera att om sidlängderna hos fyrhörningen är a, b, c, d, så finns exempel, där följden av fyrhörningar innehåller 6 icke-kongruenta: de med olika ordning på sidorna. Tag nämligenen fyrhörning med alla sidor olika, men som ändå påminner om en kvadrat (detta för att fyrhörningarna som bildas inte ska bli icke-konvexa). Men tillåtna operationer byt sedan plats på sidorna på alla möjliga sätt (trianglar med den gråa symbolen flippas):
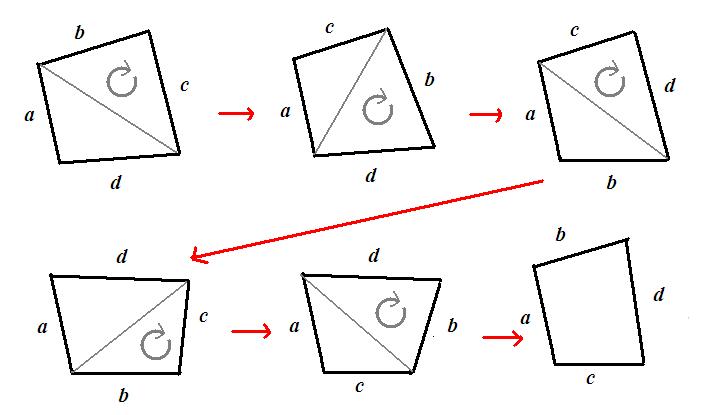
Ritningen är inte exakt, men vi kan se att alla olika sidordningar verkligen förekommer. Eftersom fyrhörningar kan roteras, valde vi fixera sidan med längden a, den kommer ändå alltid finnas.
Så nu är frågan varför det inte går att konstruera fler fyrhörningar? Notera att det finns en sak som aldrig förändras och det är summan av två motsatta vinklar i fyrhörningen. Vid varje flipp är det ett par av motsatta vinklar som inte ändras, således kommer vinkelsumman i det andra paret inte heller förändras.
Men notera också att sidlängderna kvarstår. Tag nu någon ordning på sidorna, vi skall nu bevisa att det går att bygga exakt en fyrhörning med den ordningen ur den ursprungliga. Utan inskränkning kan vi anta att sidordning är (medurs) a, b, c, d och a är den vänstra sidan.
Kalla vinkeln mellan a och d för x. Då är vinkeln mellan b och c också bestämd, nämligen S-x, där S var vinkelsumman av den ”nedre vänstra” och den ”övre högra” vinkeln. Men då har vi två trianglar, beståndsdelarna i fyrhörningen, som kan sättas ihop endast på ett sätt och det endast när de okända sidorna är lika (de ska bli en diagonal).
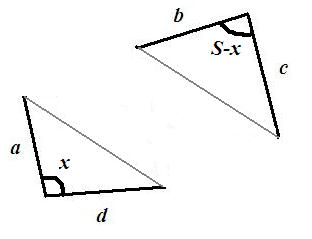
De okända sidorna är lika endast för en vinkel x (den som det går att konstruera bilden för). Det beror på att om vinkeln minskas, så minskas också den motstående sidan. Men då ökar S-x och dess motstående sida, och då kan de sidorna inte längre vara lika. Samma sak händer om vinkeln x ökas.
På så sätt har vi uttömt alla fallen och visat att antalet olika fyrhörningar är 6, en för varje sidordning.