Mattegåta
Hitta det största antalet kongruenta icke-konvexa polygoner som man kan dela in en kvadrat i, på så sätt att polygonernas sidor är parallella med kvadratens och inga två polygoner går att få ifrån varandra genom translation. Visa varför just det antalet fungerar och varför det inte går med ett större.

Orkar du rita upp ett exempel? Är inte helt hundra på vad du faktiskt menar. Ska varje sida på varje polygon vara parallell med en av kvadraternas sidor? Eller bara vissa av polygonernas sidor? Vad innebär att det inte går att ”få ifrån varandra genom translation”? Att de ”hakar fast” i varandra på något sätt?
Jag ska rita upp ett exempel snart. Men det jag menar är:
Ja, alla sidor på polygonerna ska vara parallell med någon av kvadratens (så två olika lutningar på sidorna helt enkelt). Translation innebär att man förflyttar varje punkt i en figur med en viss bestämd vektor (det vill säga det finns inga hinder, figuren ser likadan ut som i början, fast förflyttad). Alltså det som inte får förekomma är två ”parallella” polygoner.
Tack, då är jag nog med på det hela. Tolkade ”ifrån” som att de skulle tas ifrån varandra. :)
Oki :)
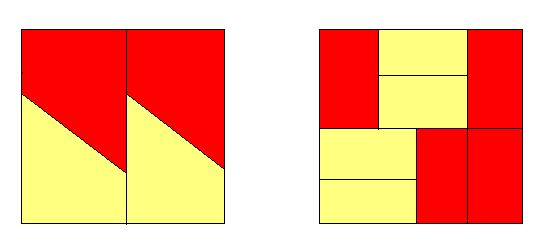
Jag kan i alla fall lägga upp de utlovade exempel:
Den vänstra bilden är fel för att:
i) polygonerna är konvexa
ii) de röda polygonerna går att få från varandra genom translation, likaså de gula
iii) inte alla polygonernas sidor är parallella med kvadratens.
Den högra bilden är fel för att:
i) polygonerna är konvexa
ii) de röda polygonerna går att få från varandra genom translation, likaså de gula.