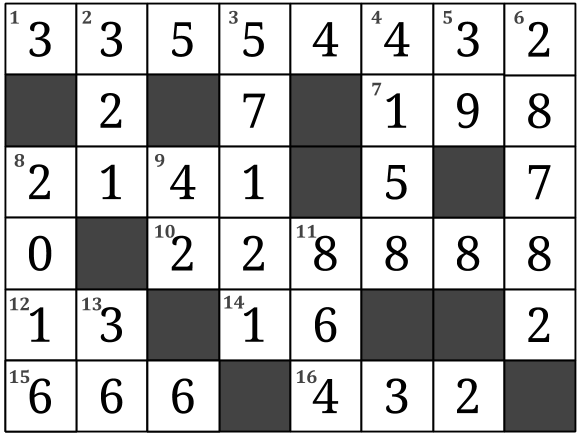
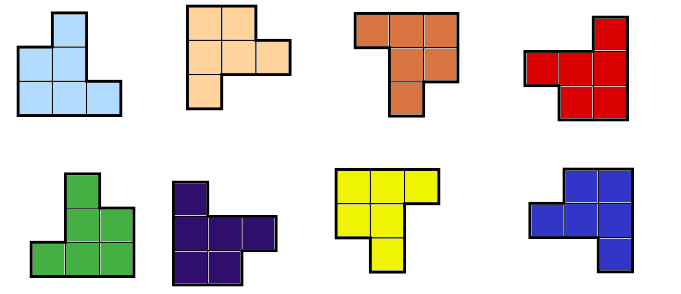
Korstal 2015
Fyll i precis som ett vanligt korsord (men endast med siffror). Obs! Inga tal börjar med noll.
Vågrätt:
1. En tvåpotens (det vill säga 2n).
7. Har samma siffersumma som vågrätt 15.
8. Talet siffersumma är lika med talets sifferprodukt.
10. Det minsta talet vars alla siffror är jämna som är delbart med vågrätt 7.
12. En delare till lodrätt 5.
14. Ett kvadrattal (det vill säga n2).
15. Alla siffrorna i talet är likadana.
16. Lodrätt 2, ökat med 111.
Lodrätt:
2. Talet siffersumma är lika med talets sifferprodukt.
3. Ett primtal i kvadrat.
4. Vågrätt 8 + vågrätt 14 + vågrätt 15 + vågrätt 16 + lodrätt 5 + lodrätt 11
5. Delbart med vågrätt 12.
6. Lodrätt 2 baklänges multiplicerat med vågrätt 16 baklänges, baklänges.
8. Vågrätt 15 + vågrätt 15 + vågrätt 15 + siffersumman för vågrätt 15
9. Delare till lodrätt 8.
11. Vågrätt 16 dubblat.
13. Ett kvadrattal.
Vad blir summan av korstalets alla trettiosju siffror?
Ladda ner Korstal 2015 som pdf
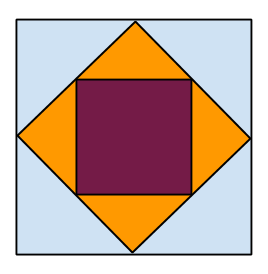
Kvadrat i kvadrat i kvadrat
Kvadrat i kvadrat i kvadrat
I en kvadrat med sidan 1 m placerade man en annan kvadrat, vars hörn hamnade precis på mittpunkterna av den första kvadratens sidor. Likadant placerade man den tredje kvadraten inuti den andra. Vilken area har den tredje kvadraten?
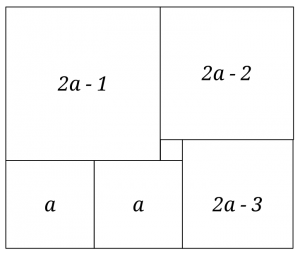
Uppdelad rektangel
Uppdelad rektangel
[kkratings]
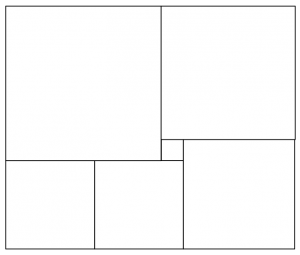
En rektangel är uppdelad i 6 kvadrater (se bilden nedan). Hur stor är den största kvadraten om den minsta har sidlängden 1cm?
Obs! Figuren är inte nödvändigvis perfekt, därför räknas det inte som en lösning att mäta längderna.
En lektion för små barn om kvadrater (och andra fyrhörningar)
Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.
Här kan du se vad vi tidigare har gått igenom.
Fyrhörningar
Vad är en fyrhörning? Hur många sidor har den och hur många hörn? Kan alla rita en fyrhörning?
Vad är en rektangel? Varför heter den så (på ryska heter det något i stil med ”rätvinkling”)? Om du ska bygga en rektangel av pinnar, vad väljer du då för längder på pinnarna?
Vad är en kvadrat? Är en kvadrat en rektangel? Är en kvadrat en fyrhörning?
Vad kallas en fyrhörning där alla sidor är lika långa? Är en romb alltid en kvadrat? Är en kvadrat alltid en romb?
Rita en romb
Alla får ett rutat papper. Börja med att sätta ut en punkt någonstans (helst i korsningen mellan två linjer). Sedan sätt ut två punkter, en till höger och en till vänster, på samma avstånd från startpunkten. Det vill säga, räkna samma antal rutor till vänster respektive till höger och sätt ut nya punkter. Gör samma sak uppåt och neråt från startpunkten, men nu kan det vara ett annat avstånd. Rita sidorna i den fyrhörningen som alla nya punkterna bildar. Du får en romb!
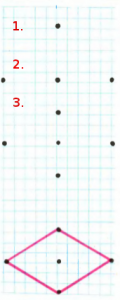
Fråga: kan man rita en kvadrat på det här sättet?
Bevisa vilken form det är
Barnen får titta på olika figurer: godtyckliga fyrhörningar som är konvexa eller konkava, rektanglar, romber, kvadrater. De måste säga alla namn som figuren kan kallas och bevisa det också, men hjälp av linjal och ett bord (med linjalen kan de mäta ifall sidorna är lika långa och medelelst bordet kan de visa att en speciell vinkel är rät).
Till exempel denna figur än en fyrhörning och en romb:
Varför fyrhörning?
– Den har fyra sidor och fyra vinklar.
Varför romb?
– Alla sidorna är lika långa (verifieras mha linjal, eller så viker man den och sätter sidorna mot varandra)
Denna figur än en fyrhörning:
Varför fyrhörning?
– Fyra sidor, fyra hörn
Varför inte rektangel?
– Två av vinklarna är räta, men inte alla fyra (rät vinkel ”bevisas” genom att sätta figuren mot bordshörnet). Eller, en annan motivering: de två motstående sidorna är inte lika långa.
Ett närmare titt på kvadrater
Alla aktiviteterna nedan handlar om kvadrater, men de är egentligen väldigt olika. En del går ut på kombinatoriskt tänkande, en del på geometriskt. Det är viktigt att tänka antal, storlek, symmetri, mönster. Och det viktigaste av allt är att vara kreativ!
Kvadratuppdelning
Hur kan man dela upp en kvadrat i fyra likadana figurer? Nedan ser ni några exempel, men egentligen finns det oändligt många sätt.
Tändsticksproblem
Tändstickorna är en klassiker!
På bilden nedan finns fem kvadrater.
Hur ska man kunna ta bort två tänkstickor, så att det blir tre kvadrater kvar? Och två kvadrater?
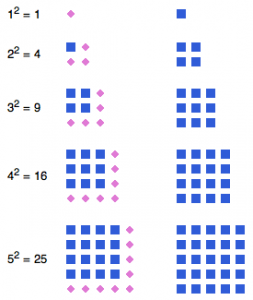
Kvadrattal
Med de äldre barnen kan vi undersöka kvadrattal. Av små kvadratiska leksakstorn får de bygga de olika stora kvadraterna en i taget. Hur mycket bygger man på i varje steg (svar: de udda talen 1,3,5,7 och så vidare).
Vika transitivt
De flesta vuxna kan få en kvadrat utav ett rektangulärt papper: man viker ihop ena hörnet så att det bildas en rätvinklig triangel (som är två lager av papper). Sedan är det bara att klippa bort/vika in den överflödiga lilla rektangeln.
Men hur gör man för att få en kvadrat av en rätvinklig triangel med inga hjälpmedel?
Och hur får man en kvadrat ut en godtycklig triangel?
Det här problemet löses i flera steg och bygga på transitivetetsprincipen. Om vi kan göra om en rektangel till en kvadrat och sedan lär oss att göra om en rätvinklig triangel till en rektangel, kan vi alltså alltid göra om en rätvinklig triangel till en kvadrat.
Godtycklig triangel -> rätvinklig triangel
Hitta en höjd inuti triangeln. Vik längs med den (det vill säga, vik ihop hörnet så att den motsatta sidans delar läggs på varandra). Voila! En rätvinklig triangel.
Rätvinklig triangel -> rektangel
Vik båda kateterna på mitten, det vill säga vik in de spetsiga hörnen. Vi har en rektangel (pga topptriangelsatsen).
Rektangel -> kvadrat
Om ena av rektangeln sidor inte är dubbel så lång eller längre som den andra, gör som ovan. Annars, vik som ovan flera gånger, tills ”restrektangeln” är tillräckligt liten. Eller klipp bort efter första steget, om sax är tillåtet.
Vika boxar
Nu när vi kan göra kvadrater av lite vad som helst, kan vi lära oss att vika ihop boxar. Fördelen med de här boxarna är att man inte behöver vara supernoggrann, för att det ska bli ett hyfsat resultat. Problemet med de små barnen och origami är att de oftast inte har precision nog att vika en vinkel exakt på hälften. Äsch, inte ens alla vuxna har den precisionen!
Adventspyssel 20
Möbelfabriken
Tre kandidater till jobbet på en möbelfabrik fick en uppgift på intervjun. De fick beskriva hur man avgör huruvida en bordskiva är formad som en kvadrat eller inte.
Den första kandidaten föreslog att man skulle jämföra bordskivans sidor med varandra, den andra tyckte att man skulle mäta diagonalerna och se ifall de var lika, den tredje tyckte däremot att man skulle jämföra de fyra strecken som bildas då diagonalerna skär varandra.
Vem av kandidaterna har störst chans att få jobbet?
Lösningen till problemet för de yngre vecka 42
Mattegåta
Till ditt förfogande har du jättemånga figurer som på bilden:
Sätt ihop
a) En kvadrat av storlek 9×9 med ett hål i mitten som är 3×3 stort.
b) En rektangel med storlek 9×12
av sådana figurer (du får vända och vrida på dem, men figurerna får inte överlappa).
Diskussion
För att förenkla arbetet med byggandet, ritar vi först upp alla möjliga utseenden på figuren när man vrider och vänder på den:
Det blev åtta möjligheter, eftersom man kan vända upp och ner på figuren och för varje vändningsläge (rättvänt eller upp-och-ner) går att det att vrida figuren på 4 olika sätt.
Konstruktionen kan påbörjas i ett hörn för både punkt a) och b). Till exempel ser vi att bara den röda och den gröna figuren passar i nedre högra hörnet.
Lösning
Nedan är lösningar för både a) och b):
Matteproblem för de yngre vecka 42
Mattegåta
Till ditt förfogande har du jättemånga figurer som på bilden:
Sätt ihop
a) En kvadrat av storlek 9×9 med ett hål i mitten som är 3×3 stort.
b) En rektangel med storlek 9×12
av sådana figurer (du får vända och vrida på dem, men figurerna får inte överlappa).
Lösningen till problemet för de äldre vecka 35
Mattegåta
Hitta det största antalet kongruenta icke-konvexa polygoner som man kan dela in en kvadrat i, på så sätt att polygonernas sidor är parallella med kvadratens och inga två polygoner går att få ifrån varandra genom translation. Visa varför just det antalet fungerar och varför det inte går med ett större.
Diskussion
Hur ska den här konstiga formuleringen tolkas?
Jo, att polygonerna har bara lodräta och vågräta sidor, så vinklarna överallt är 90 grader (eller 270). Och att alla figurera är kongruenta.
Vad betyder det att två figurer är kongruenta? Med det menas att man kan ta första figuren, flytta den på något sätt och precis täcka den andra figuren. Man får rotera och vända på den första figuren som man vill.
Faktum är att alla sådana här rörelser antingen är rotationer, speglingar, translationer eller kombinationer av de tre sakerna. Vi vet att rena translationer är förbjudna enligt uppgiften. Så det gäller att bestämma antalet sätt att rotera och spegla en figur så det alltid blir olika positionerade figurer. Sedan ska man hitta på ett exempel med det antalet också.
Lösning (av Erik Thörnblad)
Jag hävdar att åtta är det maximala antalet:
Bevis:
Rimligtvis har polygonerna hörn. Kolla på ett specifikt hörn. Kalla ena änden för A och andra änden för B. När man sedan roterar polygonen och bara tittar på just det hörnet, så framgår det att det finns totalt åtta olika sätt att vrida hörnet på, så att sidorna hela tiden är parallella med kvadratens sidor (som jag nu antagit är lodräta och vågräta).
Detta innebär att man som mest kan skapa åtta polygoner som uppfyller alla krav som ställts.
Matteproblem för de äldre vecka 35
Mattegåta
Hitta det största antalet kongruenta icke-konvexa polygoner som man kan dela in en kvadrat i, på så sätt att polygonernas sidor är parallella med kvadratens och inga två polygoner går att få ifrån varandra genom translation. Visa varför just det antalet fungerar och varför det inte går med ett större.
Lösning till problem vecka 18
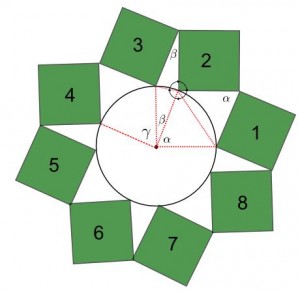
På bordet ligger en papperscirkel med radien 5 cm. Så länge det är möjligt, lägger Ilian till papperskvadrater med sidan 5 cm intill cirkeln så att följande villkor uppfylls:
1. Varje kvadrat har ett hörn som nuddar cirkeln.
2. Kvadraterna överlappar inte varandra.
3. Varje ny kvadrat nuddar den föregåendes hörn med ett hörn.
Bestäm hur många kvadrater Ilian kan lägga ut och visa, att den första och den sista kvadraten måste också nudda varandras hörn.
Jag fick in ett par fina lösningar, och jag kommer att använda mig av Erik T.’s bilder i lösningen (som ni kanske har märkt, ritar jag vanligtvis i paint, fastän jag borde ha lärt mig att TeX:a bilder för länge sen).
Lösning:
Säg att Ilian bestämmer sig för att lägga den andra kvadraten moturs från den första (det är symmetriskt ifall han lägger åt andra hållet). Det går bara att göra på ett sätt för att den nya kvadratens sida ska nudda både cirkeln och ett gammalt hörn (finns bara en punkt på cirkeln på avståndet 5 cm, som inte redan är upptagen).
Lägg på en till kvadrat, spelar inte så stor åt vilket håll, i vilket fall får vi tre kvadrater:
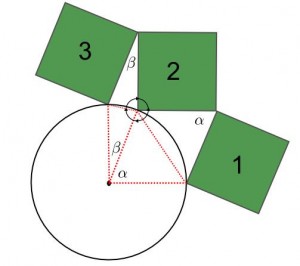
Eftersom cirkelns radie är lika med kvadraternas sidor, bildas figurer som kallas romber. En romb är en fyrkant med alla sidor lika. Man kan dela upp en romb i två trianglar och visa att trianglarna är kongruenta (sida-sida-sida). Då följer att rombens motstående vinklar är lika.
Den inringade vinkeln är 360°. Den består av en 90°-vinkel från kvadraten, samt två vinklar från var sin romb. Vinklarna från romberna är 180°-α respektive 180°-β stora. För att dessa tillsammans ska bilda en vinkel på 360°, måste α+β=90°.
Detta innebär att för varje två nya kvadrater bildas en ny 90°-vinkel runt cirkelns mittpunkt. Det finns tydligen plats för 8 kvadrater, eftersom hela vinkeln runt cirkelns mittpunkt är 360°.
α och β kommer dessutom alterneras (alla två romber bredvid varandra kommer att ge den sammanlagda vinkeln 90° runt cirkelns mittpunkt.
Således, om vi fortsätter att bygga på kvadrater kommer den nionde romben att sammanfalla med den första. Detta implicerar att den nionde kvadraten sammanfaller med den första. Alltså måste den åttonde och den första kvadraten nudda med hörnen (den åttonde och nionde gör det ju enligt konstruktionsreglerna). Så här ser det ut:
