Mattegåta
En cirkel är ritad på koordinatplanet och dess mittpunkt har koordinaterna (a,b). Man vet också att origo hamnade inuti cirkeln.
Om S+ är den totala arean av delarna i cirkeln, som består av punkter med samma tecken på koordinaterna och S– är totala arean av delarna med punkter som har olika tecken på koordinaterna, vad är S+-S– lika med?
Diskussion
När problem handlar om att jämföra areor, så är det ofta så att delar av de här areorna är lika, speciellt när delarna har konstiga former (jämför med problemet för de yngre vecka 35).
Börja med att rita den enklare varianten (då cirkelns mitt är i första kvadranten) och försök att ta bort så många lika stora delar från S+ och S– som möjligt och jämför det som blir kvar.
Lösning (av Johan Björklund, något modifierad)
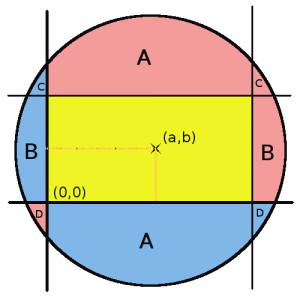
Jag tillför två hjälplinjer paralella med koordinataxlarna genom (2a,2b). De är spegelbilder av koordinataxlarna speglade genom linjer (igenom parallella med koordinataxlar) genom (a,b).
Det är lätt att se att flera av områdena har lika area (markerat med bokstäver). De kommer att ta ut varandra när vi beräknar S+-S– (S+ är den gula plus den rosa arean, medan S– är den gula plus den blå). Kvar blir den centrala rektangeln med area 4ab.
Tillägg (av Erik Svensson)
Detta var ifall mittpunkten låg i den första kvadranten. Om den istället ligger i den tredje kvadranten, då är fallet uppenbart det samma efter rotation med ett halvt varv, och ifall mittpunkten ligger i andra eller fjärde kvadranten, då speglar vi i y- respektive x-axeln och får samma fall fast med S+ och S- ombytt, så att den sökta arean byter tecken.
Vi finner emellertid att just 2a * 2b ändå uttrycker arean i samtliga dessa fall.