Nu kommer de svåraste problemen hittills! Nästa vecka återkommer jag till normal svårighetsgrad.
Skicka in lösningsförslag genom att klicka på länken under uppgifterna senast måndagen den 28 mars. Glöm inte att kolla reglerna och aktuella poängställningen.
Punkter (3 poäng). Sätt ut så många punkter på ett papper som möjligt, på så sätt att ingen trippel av punkter ligger på en och samma linje, utan utgör hörn till en likbent triangel. Du behöver inte bevisa att det inte går att sätta ut fler punkter med samma egenskap.
Likbent triangel
En likbent triangel är en triangel med två lika stora vinklar. En ekvivalent definition är att det är en triangel som har två lika stora sidor.
Här är några exempel:
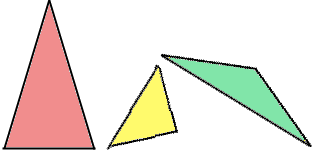
Notera att en liksidig triangel är också likbent.
Trasig våg (7 poäng). Du har 32k mynt som ser likadana ut, men bland dem finns ett falskt mynt som väger lite mindre än alla andra. Du har också tillgång till tre balansvågar (varje balansvåg har två skålar). Du vet att två vågar är i gott skick, men en är trasig och du vet inte vilken det är. Den trasiga vågen kan visa både jämvikt och ojämvikt åt ena eller andra hållet oberoende av vad du lägger på skålarna.
Hur bestämmer du vilket mynt som är falskt på 3k+1 vägningar?
Visa lösningar
Punkter (Arvids lösning):
Det maximala antalet punkter är 6 i form av en liksidig pentagon (femhörning) med en sjätte punkt mitt i centrum av pentagonen.
Trasig våg (Davids lösning): vi börjar med k=1, alltså 9 mynt och 4 vägningar. Jag ser det som välkänt (för matteintresserade) hur man hittar det falska myntet bland 3^n mynt på n vägningar med en fungerande våg. Observera att om två vågar påstår samma sak så måste påståendet vara sant. Om två vågar motsäger varandra måste en av dessa vara trasig, så den tredje vågen fungerar.
Lägg mynten i 3×3-formation. Väg första raden mot andra i våg 1. Väg första kolumnen mot andra i våg 2. Nu har vi ett misstänkt falskt mynt, i rad A kolumn B säger vi. Vi kan kalla myntet AB :) Vår tredje vägning blir (rad A men inte kolumn B) mot (kolumn B men inte rad A) i våg 3.
Om (rad A men inte kolumn B) visas som lättast: våg 2 säger att falska myntet finns i kolumn B men våg 3 säger att det inte finns i kolumn B. Motsägelsen visar att våg 1 fungerar, falska myntet finns alltså i rad A och med vår sista vägning kan vi hitta det falska myntet bland de tre kandidaterna.
Om (kolumn B men inte rad A) visas som lättast: på samma sätt vet vi att våg 2 fungerar och kan hitta det falska myntet med vår sista vägning.
Om jämvikt visas: det finns tre alternativ på vilka två vågar som fungerar. Om 1 och 2 fungerar är AB såklart falskt. Om 1 och 3 fungerar vet vi att det falska myntet finns i (rad A men inte (rad A men inte kolumn B)), en mängd bestående endast av AB. Om 2 och 3 fungerar får vi också AB som falskt. Alltså måste AB vara falskt och vi har endast använt tre vägningar.
Slutsats: antingen har vi hittat myntet på tre vägningar eller så har vi hittat en fungerande våg och kan använda den för att hitta myntet på den fjärde vägningen. Så för k=2 kan vi stapla mynten i högar om 9. Har vi hittat den falska högen efter tre vägningar så kan vi hitta det falska myntet på resterande 4 vägningar. Annars blir det lätt med hjälp av den fungerande vågen. Vi kan fortsätta med samma princip upp till godtyckligt höga värden på k.
För godtyckligt k=p, stapla i högar om 3^(2p-2). Om vi hittar den falska högen på tre vägningar har vi reducerat problemet till k=p-1. Annars har vi en fungerande våg, vi har 3p-2 vägningar kvar (vilket är större än 2p för p>2) och 3^(2p) mynt att väga = lätt.
Relaterade


Rättelse: det ska vara 3^(2k), inte 32k mynt.