Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.
Notera att barnen redan har haft två lektioner om vinklar och olika vinkeltyper.
Trianglar
Det är dags att sätta ihop punkter, sträckor och vinklar till trianglar!

Sammanbinda punkter
Uppgiften är att kopiera av punkter på bilden till sitt eget papper och sedan sammanbinda dem till en triangel. De yngre barnen får ett lika stort papper som originalet, men de äldre får en annan storlek och därmed implicit får träna skala.
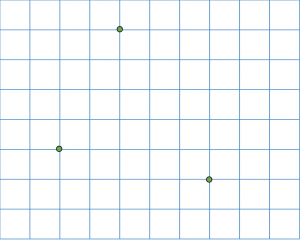
Hur många hörn har en triangel? Hur många sidor?
Hur många spetsiga vinklar kan du hitta i din triangel? Hur många trubbiga? Är det någon som har en triangel med en rät vinkel?
Efter att alla är klara med övningen kan barnen få extraövning (eller så blir det läxa): sammanbinda alla tripplar av punkter, som är av samma färg.
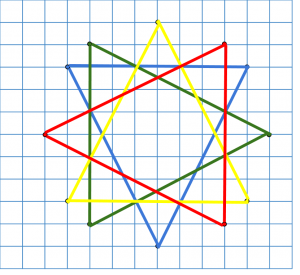
Den här bilden:
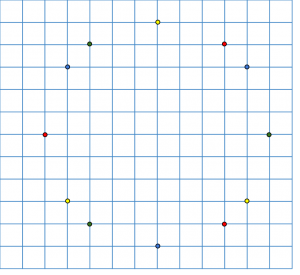
Blir till en tolvuddig stjärna:
Rita och klipp ut en egen triangel
Barnen får välja färg på pappret och ett uppdrag av mig: rita en spetsvinklig, trubbvinklig eller en rätvinklig triangel. Sedan skall trianglar klippas ut och vi ordnar dem efter storleken på den största vinkeln (först den mest trubbvinkliga triangeln, sedan andra trubbvinklig, sedan rätvinkliga etc.).
Efter det får barnen låna varandras pappersrester för att klippa ut andra trianglar och bygga ihop ett torn (som bara består av trianglar). Tillsammans tillverkar vi ”triangellandet”:

Kanske lägger jag ihop Sergels Torg – mönstret under tiden. Eller så klipper jag ut svarta och vita trianglar och barnen får arrangera dem till ”Sergels Torg”.

Triangelolikheten
Nu skall trianglar byggas av pinnar. Men det är inte alltid det går! Får man tre pinnar med längder 2cm, 3cm respektive 6cm, så går de inte sätta ihop till en triangel. Anledningen är triangelolikheten.
Barnen får en massa pinnar och skall hitta tre stycken som de kan sätta ihop till en triangel (med häftmassa till exempel). De äldre barnen ska försöka förklara när det går att bygga en triangel och när det inte går.
Vägar
Apropå triangelolikheten kan vi prata om den kortaste vägen och det kortaste avståndet med 7- och 10-åringarna. Hur kan man t.ex. avgöra om ens handled eller fotled är smalare (t.ex. med snöre)? Med samma hjälpmedel kan man avgöra vilket har större omkrets: en cirkel eller en liksidig triangel, inskriven i cirkeln?
Vilken väg från dörren till fönstret är kortast (notera att bord kan vara i vägen för den raka sträckan)?

Bygga med en magnetisk struktur
Vi avslutar med att pyssla med en magnetisk byggsats, där bitarna är magnetiska pinnar och kulor, som binds ihop väldigt starkt med varandra. Vilka former på trianglar går att bygga med hjälp av byggsatsen? Går det att bygga 3D-strukturer som består av trianglar och i så fall vilka? (T.ex. en tetraeder eller en ikosaeder går att bygga.) För de äldsta barnen berättar jag om de platonska kropparna som finns och vi försöker bygga dem alla.

Notera att jag antagligen inte hinner med allt ovanstående på alla lektioner. Ibland fastnar barnen på en sak, ibland blir uppgiften för svår. Men det mesta kommer ändå med på lektionerna.

Den sista uppgiften är speciellt spännande eftersom man kan efterlikna olika typer av ytor genopm att klistra trianglar. Klistrar man trianglar så att det är 6 stycken trianglar kring varje hörn såfår man ett plan. Klistrat man färre antal trianglar som bilden där vi har 5 trianglar/hörn eller en tetraeder där det är 3 trianglar/hörn så får man något som påminner om en väldigt kantig sfär. Matematiskt sett så säger man att en sfär har en positiv krökning medans planet har krökning noll. Man kan också tänka sig en yta med negativ krökning, det hyperboliska planet. Det går inte riktigt att framställa i vårt vanliga rum, men det går att få en känsla för det genom att klistra 7 (eller fler) trianglar per hörn och sedan fortsätta att göra det. det man får kommer då att bete sig ungefär som ett hyperboliskt plan. Ganska rolig laboration för lite äldre elever. Krökningen är kopplad till vinkelsummor hos trianglar, medans trianglar i plan har vinkelsummor som är precis pi radianer så har trianglar på sfärer större vinkelsummor och trianglar i hyperboliska plan mindre vinkelsummor.
Häftigt, Johan! Har du provat att klistra ihop 7 trianglar själv? Tror du att det funkar bra med vanligt papper eller kartong?
Jag har inte provat det själv (ännu!) men jag har sett en modell som Georgios använde då han föreläste om det på Kovalevskydagarna för några år sedan.
Jag tror man bör använda papper snarare än kartong då det är bra om ytan kan böja sig.