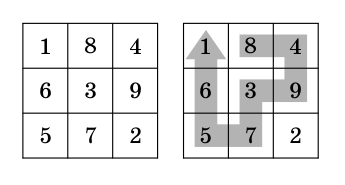
Siffrorna 1 till 9 fyller kvadraten som det syns på den vänstra bilden. Man får gå på kvadratens rutor, men aldrig tillbaka till en ruta man varit på förut, och man måste alltid gå till en angränsande ruta.
Katarina gick längs med pilen som syns på den högra bilden. Hon skrev ner siffrorna som hon gick på i ordning och fick talet 84937561. Rita en annan väg, som ger ett större tal (ju större tal, desto bättre).
Notera att ett tal är desto större, ju fler siffror det har. Så det går att förbättra Katarinas resultat, om vår pil går genom alla nio siffrorna.
Ju högre siffra talet börjar på, desto större är talet. Men vi kan inte börja pilen på 9:an och samtidigt gå på alla de 9 rutorna, ty vi inte kan börja på någon svart ruta alls. Börjar vi på en svart ruta, måste vi även sluta på en svart, alltså gå på 5 svarta respektive 4 vita rutor. Men 5 svarta rutor finns inte ens!

Vi börjar på den största möjliga rutan, det vill säga 5. Har vi ett val, går vi till en större siffra, för att maximera talet. Vi börjar alltså gå 5-7-4. Men går vi sedan till 9, kommer vi inte kunna gå på alla nio rutorna. Samma sak gäller om vi går till 8. Så vi måste gå till 6, och sedan är vägen entydigt bestämd: 5-7-3-6-1-8-4-9-2.
Största talet man kan få är alltså 573618492.


Anses två rutor vara angränsande omm de har en gemensam sida, eller räcker det med att de ligger hörn i hörn?
Det måste vara gemensam sida.
Jag älskar verkligen den här kluringen! Superrolig, ganska enkel, men mycket nyttig. :D Vacker helt enkelt. :D
Jag förstår hur du menar Lisa och håller helt med :)
Uppgifterna från den tävlingen (Moskvas matematikolympiad för de yngre årskurserna) är väldigt vackra.