Ett lejon springer runt på en rund cirkusarena, som har radien 10 m. Lejonets bana består av raka streck och i slutändan springer han 30 km. Visa att summan av alla vinklar, som lejonet svängde under springturen, är minst 2998 radianer.
Säg att  är sträckorna som lejonet springer på, medan
är sträckorna som lejonet springer på, medan 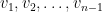 är vinklarna som han svänger på. Betrakta lejonets bana på följande sätt.
är vinklarna som han svänger på. Betrakta lejonets bana på följande sätt.
Låt han springa sträckan 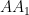 med längden
med längden 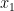 . Rotera då arenan kring lejonet, det vill säga punkten
. Rotera då arenan kring lejonet, det vill säga punkten 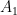 , med vinkeln
, med vinkeln 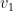 , på så sätt att sträckan
, på så sätt att sträckan  blir en fortsättning på sträckan
blir en fortsättning på sträckan 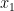 . Efter att lejonet sprunget sträckan
. Efter att lejonet sprunget sträckan  , rotera arenan med vinkeln
, rotera arenan med vinkeln  , så att
, så att 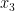 utgör fortsättningen utav
utgör fortsättningen utav  , och så vidare. I så fall springer lejonet rakt fram hela tiden och totalt sett springer han sträckan
, och så vidare. I så fall springer lejonet rakt fram hela tiden och totalt sett springer han sträckan 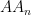 , som är 30000 meter lång.
, som är 30000 meter lång.
Hur arenans mittpunkt 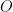 rört sig under tiden? Först roterar
rört sig under tiden? Först roterar 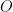 kring punkten
kring punkten 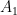 med vinkeln
med vinkeln 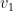 , sedan kring
, sedan kring  med vinkeln
med vinkeln  och så fortsätter det på samma sätt.
och så fortsätter det på samma sätt. 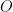 är aldrig längre bort än 10 meter från rotationens centrum, eftersom rotationens centrum är lejonet, som alltid befinner sig inuti arenan. Därför kommer
är aldrig längre bort än 10 meter från rotationens centrum, eftersom rotationens centrum är lejonet, som alltid befinner sig inuti arenan. Därför kommer 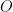 som mest flyttast
som mest flyttast 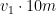 vid första rotationen,
vid första rotationen, 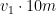 vid andra och så vidare (om
vid andra och så vidare (om  mäts i radianer). Så
mäts i radianer). Så 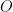 kommer maximalt att flyttas
kommer maximalt att flyttas  . Alltså:
. Alltså:
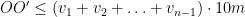 .
.
Startarenan ger oss  , slutarenan ger
, slutarenan ger  .
.
Och då, eftersom 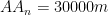 , så är
, så är 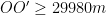 . Således har vi att:
. Således har vi att:
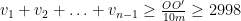 radianer.
radianer.


Går det att göra på under 2999 radianer? Minsta jag hittar är ca 2999,32.
Kolla om det går att uppnå likhet i olikheterna i lösningen.
Vilket är ditt sätt?
Ska kolla närmare på det, men vid första anblicken ser det svårt ut att få likhet tycker jag. Mitt sätt är så här: låt lejonet starta i en punkt på cirkelns rand, riktat så att vinkeln COD är pi/6, där C är cirkelns mittpunkt, O lejonets startposition och D en valfri punkt som lejonet är riktat mot. Lejonet springer tills han åter når cirkelns rand, då har han sprungit 2*10*cos(pi/6) = 10*sqrt3 meter och ännu aldrig svängt. Därefter vill han approximera cirkelrörelse längs med cirkelns rand ända tills han är klar. Om vi antog att cirkelrörelse var möjlig skulle han först behöva svänga pi/3 radianer för att hamna i tangent med cirkeln och sen springa 30000-10*sqrt3 meter vilket kräver 3000-sqrt3 radianer. Totalt svänger han alltså pi/3+3000-sqrt3 radianer. Han kan komma godtyckligt nära detta med små raka streck.
Likhet borde väl aldrig kunna uppnås eftersom den maximala förflyttningen av cirkelns mittpunkt vid en rotation med vinkel v är 20*sin(v/2) < 20*v/2 = 10v (det är ju förflyttningen längs cirkelbågen som är maximalt 10v men det faktiska avståndet mellan startpunkt och målpunkt är mindre). Så om jag inte tänker fel är det strikt olikhet i första olikheten.
Ja, det är sant det du skriver, David. Förflyttningen av O kan inte nå upp till 10v, alltså kan inte likheten nås.
Och med din metod (först springa en rak sträcka och sedan springa ”längs med” cirkeln) uppnås minimum vid just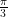 . Den metoden verkar dessutom logisk för att ha mycket avstånd vs vinkelsumma, så jag kommer inte på någon förbättring.
. Den metoden verkar dessutom logisk för att ha mycket avstånd vs vinkelsumma, så jag kommer inte på någon förbättring.
Man kan ha LaTeX i kommentarerna för övrigt.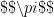 blir
blir 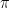 till exempel.
till exempel.