Kvaternioner

Enligt en broinskription (se bilden nedan) upptäcktes kvaternionerna för exakt 169 år sedan, då William Hamilton tog en promenad i Dublin med sin fru. Hamilton kände till de komplexa talen (till exempel talet i som uppfyller likheten i\cdot i = -1), men han ville utvidga dem ytterligare till en större talmängd, som fortfarande skulle uppfylla de viktigaste talegenskaperna.

Han kom då på mängden kvaternioner (betecknas \mathbb{H}), som förutom vanliga tal och i även innehåller talen j och k, som uppfyller följande:

(i\cdot i = -1 , denna egenskap är kvar från de komplexa talen)
j\cdot j = -1
k\cdot k = -1

i\cdot j = k
j\cdot k = i
k\cdot i = j

Det spelar förstås ingen roll vilka bokstäver man väljer att beteckna de här nya talen med, det viktiga är deras egenskaper och samverkan med varandra.

Notera att multiplikationen talen emellan är lite märklig. Desto märkligare är att i\cdot j inte blir samma sak som j\cdot i, det vill säga Hamilton lyckades inte behålla multiplikationens kommutativitet. Man adderar och subtraherar dock kvaternioner precis på samma sätt som man skulle göra med de komplexa talen. Man kan addera de olika bokstäverna med varandra och exempelvis gäller:
(1+2i+j) + (2+i-j+k) = 3+3i+k

Hur kan vi lista ut vad j\cdot i bör bli lika med? Tänk på att vi inte kan byta plats på faktorerna, men vi kan multiplicera med något nytt ”från vänster” eller ”från höger”. Säg att vi multiplicerar med i från höger:

(j\cdot i)\cdot i = j\cdot (i\cdot i) = j\cdot (-1)=-j

Så att vårt svar multiplicerat med i från höger ska också vara lika med -j. Vad kan det vara för tal?
Om du inte kan komma på det, tänk på vilket tal multiplicerat med i från höger blir lika med j istället och modifiera svaret efter det.

Man kan göra en liten grundmultiplikationstabell för de komplexa talen:

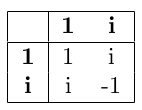
Kan du lista ut vad som står istället för frågtecknen i multiplikationstabellen för kvaternionerna?

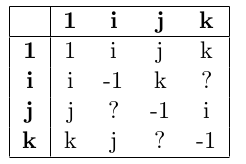
En övning i kvaternioner: Vad blir (1+i+j)(2-j+k)?

Det går att dividera kvaternioner med varandra, resultatet av en division blir alltid ett kvaterniontal (så länge man inte dividerar med 0).

En till övning: Vad blir 1/(i+j) för kvaterniontal?

2 reaktioner till “Kvaternioner”

Lämna ett svar

Denna webbplats använder Akismet för att minska skräppost. Lär dig hur din kommentardata bearbetas.

© 2009-2024 Mattebloggen