Roliga mattegåtor – Sida 15

Ädelstenar

[kkratings]

Dario fick en stor säck i julklapp av en väldigt rik person. I säcken ligger sjukt många ädelstenar, gröna och gula, men han kan inte avgöra på formen vilken färg de har. Dario tar ut 100 ädelstenar på måfå först och sedan 10 ädelstenar på måfå. När är sannolikheten större att han får lika många stenar av varje färg: i första eller andra fallet?

Visa lösningen

Trigonometrisk rebus

Dagens gåta är en sifferrebus. Notera att trigonometriska ”formeln” inte stämmer.

Trigonometrisk rebus

[kkratings]

Kevin ställde upp en addition, men sedan döljde uträkningen genom att byta ut siffror mot bokstäver (likadana siffror byttes ut mot samma bokstav och olika byttes ut mot olika).

Kan du återställa uträkningen?

Visa lösningen

Bräde

[kkratings]

Ett bräde är indelad i 4×4 rutor. Du får såga längs med de små rutdiagonalerna (det går bra att såga i båda diagonalerna på en vissa ruta). Hur många små diagonaler kan du som mest såga utan att brädet faller isär i bitar?

Visa lösningen

Rektangel

[kkratings]

Du har tillgång till 12 sträckor som är 2cm långa, 12 sträckor som är 3cm och 11 sträckor med längden 5cm. Går det att bygga en rektangel av alla sträckorna med sidlängderna lika med ett helt antal centimeter?

Visa lösningen

Tre brev

Du har fått tre brev och måste omedelbart äta upp ett av dem. I varje brev finns en lapp med två meningar. I ett av breven är båda meningarna goda råd, i ett annat är båda dåliga råd och det tredje innehåller ett gott och ett dåligt råd. Så här stod det i breven:

Brev 1:
1. Du ska inte äta det här brevet
2. Det är nödvändigt att äta det andra brevet

Brev 2:
1. Det första brevet ska inte ätas
2. Är det tredje brevet!

Brev 3.
1. Man borde inte äta det här brevet
2. Ät gärna det första brevet

Vilket brev borde ätas upp?

Visa lösningen

Femkronors-spel

Erik och Sixten spelar ett spel mot varandra. Reglerna är enkla: de turas om att lägga femkronors-mynt på ett runt bord (som från början är tomt). Mynten som redan är lagda ligger kvar till slutet av spelet. Den pojken, som inte kan göra ett drag, förlorar spelet.

Det första draget är Eriks. Kommer han att vinna om båda pojkarna spelar på bästa möjliga sätt?

Visa lösningen

Filmtitlar

Rebusarna motsvarar filmtitlar på engelska. Försök att lista ut så många du kan!

Problem vecka 21

Matchen (2 poäng).
Innan fotbollsmatchen mellan lag Syd och lag Nord fanns det 5 prognoser:
a) det kommer inte att bli oavgjort
b) Syd kommer att släppa in mål
c) Nord kommer att vinna
d) Nord kommer inte att förlora
e) det kommer bli exakt 3 mål i matchen

Efter matchen visade det sig att exakt tre prognoser stämde. Vad blev matchens resultat?

Dvärgarna (4 poäng).
Draken fångade sex dvärgar, låste in dem i sin grotta och sade till dem: ”Jag har sju hattar som har var sin färg: röd, orange, gul, grön, blå, lila och vit. Imorgon vid gryningen kommer jag att binda för era ögon och sätta var sin hatt på er och en hatt gömmer jag. Efter det kommer ni att kunna se, men ni får inte längre prata med varandra. Sedan får var och en viska till mig, vilken färg det är som saknas. Om åtminstone tre stycken gissar rätt, befrias ni alla. Om färre gissar rätt, äter jag upp er alla.”

Vad ska dvärgarna bestämma innan gryningen, för att rädda sig själva?

Rutnätet (6 poäng).
Varje punkt med heltalskoordinater på planet målades i en av tre färger. Visa att det går att hitta en likbent rätvinklig triangel med hörn i punkter med heltalskoordinater, som är målade i samma färg.

Visa lösningar

Matchen (Oves lösning):
Om Nord vinner då är a),b),c) och d) sanna.
Om det är oavgjort så är a), c) och e) falska (då tre mål ej kan fås vid oavgjort).
Alltså eftersom att exakt 3 ska vara sanna, måste Syd vinna, eftersom ingen av de andra fallen fungerar.

Så Syd släpper in mål och det görs exakt 3 mål i matchen och Syd vinner, så då måste det bli 2-1 till Syd.

Dvärgarna (Davids lösning):
Varje dvärg ser alla färger utom sin egen och den som saknas. Av de två färger man inte ser säger man den som vinner. Vilken vinner då?

Röd vinner över orange, gul och grön.
Orange vinner över gul, grön och blå.
Gul vinner över grön, blå och lila.
Grön vinner över blå, lila och vit.
Blå vinner över lila, vit och röd.
Lila vinner över vit, röd och orange.
Vit vinner över röd, orange och gul.

Oavsett vilken färg som saknas så vinner den över exakt tre av dvärgarnas färger. Alltså kommer exakt tre dvärgar säga rätt färg.

Rutnätet
Om vi kollar på en kvadrat med sidan 4 punkter (bestående av 16 punkter), måste två av punkterna på dess diagonal ha samma färg.

Det finns ändligt många sätt att färglägga med sidan 4 punkter med 3 färger, så det finns ett m, som är större än det antalet. Det vill säga, en kvadrat bestående av m^2 kvadrater med sidan 4 har två exakt likadant färgade kvadrater på sin diagnoal (här består diagonalen av kvadrater med sida 4). De stora kvadratens sida består av 4m punkter.

På samma sätt hittar vi en ännu större kvadrat K, som har två likadant färgade kvadrater med sidan 4m på diagonalen.

Antag att det inte finns några rätvinkliga likbenta trianglar med hörnen i samma färg. Vår kvadrat med sidan 4m som har två likadant färglagda små kvadrater på diagonalen har följaktligen 4 punkter med färg ett, 2 punkter med färg två och således 1 punkt av färg tre som kan ses på bilden.

På samma sätt tittar vi på kvadraten K, som då måste ha en ruta, som varken kan ha färg ett, färg två eller färg tre. Motsägelse, alltså måste vi någonstans ha en likbent rätvinklig triangel med hörnen färgade i samma färg.

Problem vecka 20

Cthulhu (1 poäng).
”Ni alledels för små för att se detta”, sade Cthulhu till sina 33 barn och skrek ut ”Blunda!”. Alla pojkarna blundade med högerögat, likaså en tredjedel av flickorna. Alla flickorna blundade med vänsterögat, likaså en tredjedel av pojkarna. Hur många barn såg ändå det som de var för små för att se?

Tabellen (3 poäng).
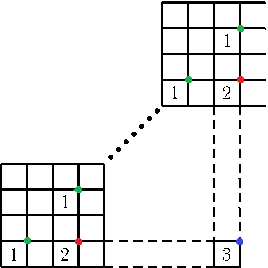
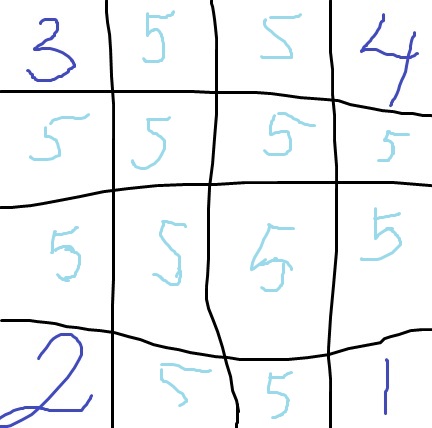
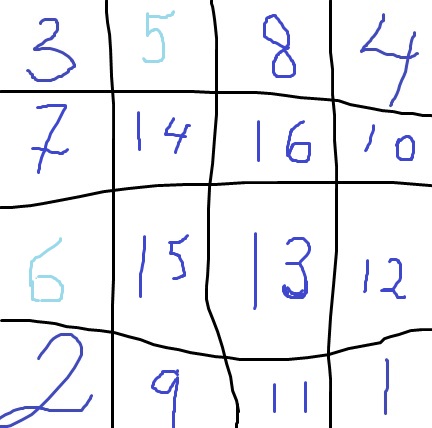
En 4×4-tabell är fylld med talen från 1 till 16. I varje rad, varje kolonn och varje diagonal (inklusive diagonalerna som består av en ruta) är det största talet markerat. Ett och samma tal kan alltså bli markerat flera gånger. Kunde det bli så att
a) alla tal utom två blev markerade?
b) alla tal utom ett blev markerade?
c) alla tal blev markerade?

Stenhögarna (5 poäng).
Det finns tre stenhögar. Sisyfos rullar en sten i taget från en hög till en annan. För varje sten han överför får han ett antal guldmynt från Zeus, som är lika med skillnaden mellan antalet stenar i målhögen och antalet stenar i starthögen (stenen, som rullas mellan högarna, räknas inte in). Om skillnaden är negativ, lämnar Sisyfos tillbaka en respektive summa till Zeus. Om Sisyfos inte kan betala, låter den välvillige Zeus honom att vara skyldig pengarna.

En gång blev det så att alla stenarna hamnade i samma högar, som de fanns i från början. Hur mycket kunde Sisyfos som mest ha tjänat då?

Visa lösningar

Cthulhu (Toomas lösning):
Vi kan notera att en tredjedel av barnen blundade med båda ögonen, det vill säga 33/3=11 stycken. Antalet barn som ändå såg den givna händelsen var då 33-11=22.

Tabellen (Lisas lösning):
Alla tal kan aldrig bli markerade. För att ettan ska kunna bli markerad måste den finnas i ett hörn för att bli störst i diagonalen på en ruta. Det innebär att även tvåan måste befinna sig i en hörnruta. Detta leder i sin tur att även trean måste vara det eftersom den annars aldrig kan befinna sig i en rad, kolumn eller diagonal där den är störst. Samma gäller fyran. Därefter, var man än placerar femman så kommer den aldrig kunna vara störst i sin rad, kolumn/diagonal eftersom det varje ledig rad/kolumn/diagonal finns plats för fler tal.

Alla utom ett tal kan bli markerade. Det har jag visat genom genom ifyllning av tabellen nedan. Jag lät femman vara utan markeringar och fyllde i resterande siffror på så sätt att varje nytt tal (större än det före detta ifyllda) fick bli störst i en rad, kolumn eller diagonal.

Alla utom två tal kan också bli markerade. Det har jag visat i tabellen nedan. Jag fyllde i rutorna på samma sätt som ovan, men såg först till att placera sexan i en rad/kolumn/diagonal där den inte skulle kunna vara störst.

Svar: a) Ja. b) Ja. c) Nej.

Stenhögarna (Davids lösning):
Istället för att säga att han får betalt med skillnaden så säger vi så här: när han flyttar en sten från en hög måste han betala lika många guldmynt som det finns stenar kvar i högen han flyttade från. När han flyttar en sten till en hög får han betalt med lika många guldmynt som det redan fanns stenar i högen han flyttade till. Detta blir samma sak, men ett lite annorlunda sätt att se på saken. Betrakta nu en given hög med stenar och alla överföringar som görs till eller från den högen. Varje gång en sten flyttas därifrån får Sisyfos betala, varje gång en sten flyttas dit får han betalt. Vi vet att det finns lika många stenar i högen i vår slutsituation som det fanns när vi började. Jag vill visa att den totala summan pengar som Sisyfos har tjänat på den givna högen alltid är 0.

Det räcker att visa att påståendet gäller för första gången han återvänder till lika många stenar som det fanns från början. Om det alltid gäller att han tjänat 0 vid första gången han återvänder, så måste det även gälla för alla gånger efter det: han måste ha tjänat 0 mellan första och andra gången, mellan andra och tredje gången o.s.v.

Vidare räcker det enligt samma resonemang att visa att påståendet gäller för första gången han återvänder till något läge som han redan befunnit sig i. Alltså att första gången som det finns två olika tidpunkter då det finns lika många stenar, så har han tjänat 0 mellan dessa två tidpunkter. Om vi kan visa det så kan vi helt bortse från tiden som förflutit mellan dessa två tidpunkter och inse att det måste gälla även nästa gång och nästa och nästa…

Men första gången han återvänder till ett tidigare läge kan endast ske på två sätt:
a) först tar han bort en sten från högen och därefter lägger han till en sten i högen.
b) först lägger han till en sten i högen och därefter tar han bort en sten från högen.

Låt det finnas x stenar i högen. I a) får han då först betala x-1 och därefter får han betalt x-1. I b) får han först betalt x och därefter får han betala x. I båda fallen blir summan 0 vilket skulle visas.

Vi har nu visat att han för varje hög har tjänat exakt 0. Därför är den totala summan som han tjänat för alla högar också exakt 0.

Problem vecka 19

Uttrycket (3 poäng).
Man utvecklade uttrycket (x+y)^n med hjälp av binomialsatsen. Den andra termen i summan blev lika med 240, den tredje blev lika med 720 och den fjärde blev lika med 1080. Hitta x, y och n.

Ön (7 poäng).
a) På en platt cirkelformad ö finns 4 hamnar (i den ordningen): 1, 2, 3 och 4. Mellan dem finns vägar där det kan finnas korsningar, det vill säga punkter där vägarna möts, korsas eller grenas. På alla sträckor är trafiken enkelriktad, på så sätt att man aldrig kan komma tillbaka till en hamn eller korsning om man startar därifrån. Låt f_ij beteckna antalet vägar som går från hamn i till hamn j.
Visa olikheten f₁₄f₂₃≥f₁₃f₂₄
b)

Visa att om det finns 6 hamnar (1, 2, 3, 4, 5, 6 i den ordningen) så gäller

f₁₆f₂₅f₃₄+f₁₅f₂₄f₃₆+f₁₄f₂₆f₃₅≥f₁₆f₂₄f₃₅+f₁₅f₂₆f₃₄+f₁₄f₂₅f₃₆

Visa lösningar

Uttrycket (Toomas lösning, kompletterad):
Vi har alltså en utveckling av ett binom (x+y) upphöjt i ett tal n enligt binomialsatsen sådant att den andra termen är lika 240, den tredje 720 och den fjärde lika 1080.

Vi förnimmer oss att binomialsatsen kan skrivas

$(x+y)^n = {n \choose 0}x^n y^0 + {n \choose 1}x^{n-1}y^1 + {n \choose 2}x^{n-2}y^2 + \cdots + {n \choose n-1}x^1 y^{n-1} + {n \choose n}x^0 y^n$

Detta innebär att om vi ersätter den retoriska notationen i problemtexten med symbolisk algebra får ekvationssytemet

${n \choose 1}x^{n-1}y^1=240$

${n \choose 2}x^{n-2}y^2=720$

${n \choose 3}x^{n-3}y^3=1080$

som förstås kan förenklas till

$nx^{n-1}y=240$

$\frac{1}{2}(n^2-n)x^{n-2}y^2=720$

$\frac{1}{6}(n-2)(n-1)nx^{n-3}y^3=1080$

Dividera den andra ekvationen med den första, samt den tredje ekvationen med den andra:

$\frac{1}{2}(n-1)\frac{y}{x}=3\ \ \Rightarrow \ \ (n-1)y=6x$

$\frac{1}{3}(n-2)\frac{y}{x}=\frac{3}{2}\ \ \Rightarrow \ \ (n-2)y=\frac{9}{2}x$

Subtrahera den andra ekvationen från den första

$y=\frac{3}{2}x$

och gör en ersättning i en av ekvationerna för att få n:

$(n-1)\frac{3}{2}x=6x\ \ \Rightarrow \ \ n-1=4 \ \ \Rightarrow \ \ n=5$

Nu kan vi göra ersätta n med 5 i den första ursprungliga ekvationen:

$5x^4\frac{3}{2}x=240 \ \ \Rightarrow \ \ x^5=32 \ \ \Rightarrow \ \ x=2$

$y=\frac{3}{2}\cdot 2=3$

Den enda lösningen är alltså n=5, x=2 och y=3.

Ön (Skäggets lösning, något modifierad):

a) Vi noterar att f₁₃*f₂₄ kan ses som antalet sätt man kan gå från 1 till 3 och sedan från 2 till 4, och att f₁₄*f₂₃ är antalet sätt man kan gå från 1 till 4 och sedan från 2 till 3.

En väg från 1 till 3 delar vår ö i två delar, med 2 och 4 på olika sidor. Således måste en väg från 2 till 4 korsa varje väg från 1 till 3 vid minst en punkt.

Tag en godtycklig väg som går från 1 till 3 (kalla den A) och sedan magiskt fortsätter vid 2 och går till 4 (via en väg B). A och B måste korsa varann i någon punkt X (vi kan exempelvis välja den första korsningen på A).

Antag att vi börjar från 1 och följer A tills vi når X. Sedan fortsätter vi längs väg B tills vi når 4. Sedan hamnar vi på något magiskt vis i 2 och följer B tills vi når X, och följer sedan A till 3.

Vi ser att för varje sammansättning A och B får vi en väg från 1 till 4 och sedan 2 till 3. Detta ger upphov till en funktion som uppenbart är injektiv (två vägar måste ju ha identiska vägsegment såväl före som efter X för att ett vägskifte vid X ska ge samma resultat, och då är de samma väg).

Således har vi en injektiv funktion från mängden av vägar 1-3-2-4 (med magiskt hopp från 3 till 2) och mängden av vägar 1-4-2-3 (med magiskt hopp från 4 till 2). Dessas mängders storlekar är som vi noterat f₁₃*f₂₄ respektive f₁₄*f₂₃, och således har vi visat olikheten i fråga.

b)Vi ser att vänsterledet kan ses som unionen av alla vägar 1-6-2-5-3-4 och 1-5-2-4-3-6 och 1-4-2-6-3-5 (med magiska hopp), sådana vägar kallar vi udda. Högerledet kan ses unionen av alla vägar 1-6-2-4-3-5 och 1-5-2-6-3-4 och 1-4-2-5-3-6, sådana vägar kallar vi jämna. Om två hamnar med nummer 4, 5 eller 6 byter plats i en väg, byter vägen paritet.

Tag en väg 1-x-2-y-3-z, där {x,y,z} är en permutation av {4,5,6}. Om delsträckorna skär varandra någonstans, kalla skärningspunkten närmast 1 för M (det vill säga skärningspunkten som kommer först på sträckan 1-x om den sträckar korsar andra, annars skärningspunkten närmast 2 på sträckan 2-y). Byt plats på vägsluten efter punkten M, precis som i punkt a). (Om alla delsträckorna går genom M bestämmer vi en regel om att alltid byta plats på vägsluten av desträckorna 1-i och 2-j.)

Om man byter två stycken vägslut byter vägen paritet. På så sätt har vi bestämt en bijektion mellan udda och jämna vägar som har korsningar. Varje väg som inte har korsningar är dessutom en udda väg av typ 1-6-2-5-3-4. Därför finns det minst lika många udda vägar som jämna. Av det följer olikheten.