Roliga mattegåtor – Sida 25

Spiken i lådan

Rekommenderad från: 11 år

[kkratings]

Cissi klippte ut två likadana figurer ur en stor kartong. Sedan la hon dem på bottnen av en rektangulär låda så att de delvis täckte varandra. Det visade sig att hela bottnen blev täckt.

Sedan slog Kalle in en spik i mitten av lådans botten. Kunde det bli så att spiken gick igenom ena figuren, men inte den andra?

Visa lösningen

Tvåpotensens sista siffra

Rekommenderad från: 15 år

[kkratings]

Det finns ett naturligt tal m, sådant att talet 2^m har siffersumma 8. Kan sista siffran i talet 2^m vara lika med 6?

Visa lösningen

Svar:

Det kan den inte! Jag har fått in tre stycken olika lösningar, så det är bara att välja och vraka.

För att kunna förstå lösningarna är det bra att kunna:

moduloräkning

Om två tal har lika rester vid division med ett och samma tal n, så säger man att de talen är kongruenta modulo n.

Till exempel så är talen 3 och 11 kongruenta modulo 4 eftersom båda ger rest 3 när man dividerar med 4. Även talet -1 är kongruent med 3 modulo 4.
Man kan också skriva 3 $\equiv$ 11 (mod 4)

delbarthetsprincipen för 3

Ett heltal är delbart med 3 om och endast om dess siffersumma är delbar med 3. Man kan också vara fancy och säga att ett tal är delbart med 3 om och endast om talets siffersumma är kongruent med 0 modulo 3.

Till exempel så är talet 450072456 inte delbart med 3, eftersom siffersumman är 4+5+0+0+7+2+4+5+7=34 och det talet går inte att dela jämnt på 3.

delbarthetsprincipen för 9

Liknar faktiskt delbarthetsprincipen för 3. Ett heltal är delbart med 9 om och endast om dess siffersumma är delbar med 9.

Till exempel så är talet 1111000011111 delbart med 9, eftersom siffersumman är lika med 9.

Det är även så att ett godtyckligt tal och dess siffersumma alltid ger samma rest vid division med 9, det vill säga det är kongruenta modulo 9.

Lösning 1 (den officiella):

Vi konstaterar att de första tvåpotenserna är 2, 4, 8, 16 och 32, samt att inget av dessa uppfyller kriterierna. Dock måste alla kandidater vara jämnt delbara med dessa tal.

Om ett tal har siffersumman 8 och slutar på 6 finns två möjligheter:

a) Talet har formen 2*10^k + 6 för något k>=1 (dvs 26, 206, 2006, osv.)

26 (=2*13) är inte en tvåpotens, alltså måste k>=2, men alla andra tal på formen
2*10^k är delbara med 8, medan 6 inte är delbart med 8. Således blir talet som
helhet (2*10^k + 6) ej delbart med 8. Vi kan alltså helt utesluta denna möjlighet.

b) Talet har formen 1*10^k + 1*10ⁿ + 6 för något k>n>=1 (dvs på formen 100..0100…06)

6 är inte delbart med 4, så resten får inte heller vara det, om summan skall vara delbart med 4. Det enda n sådant att 10ⁿ inte är delbart med 4 är n=1 (k kan inte vara så litet). Alltså måste talet ha formen 1*10^k + 16.

Vi ser dock på samma sätt att 16 inte är delbart med 32, så det får inte 10^k heller vara. För alla k>=5 är 10^k jämnt delbart med 32, så dessa förkastas.

Man kan nu pröva de återstående lösningarna (10016, 1016, 116) var och en, men närmare bestämt är 16 $\equiv$ 16 i modulo 32, så 10^k måste vara lika med 32-16 $\equiv$ 16 (mod 32). Det enda k som uppfyller detta är k=4, vilket ger 10016 = 2⁵ * 313, som på intet vis är en tvåpotens. För säkerhets skull kan konstateras att 1016=2³*127 och 116=2²*29.

Lösning 2 (den med perioder):

Att siffersumman av 2^m 8, kräver att 2^m är kongruent med 8 modulo 9.

Att 2^m slutar på 6, kräver att 4|m. Detta ser man genom att helt enkelt
göra en tabell av potenser av 2, och ser att den har period 4, om man bara
betraktar sista siffran.
2, 4, 8 (1)6, (3)2,(6)4, (12)8, (25)6,…

Så, vi undrar egentligen om det finns heltal k, så att 2^4k $\equiv$ 8 (mod 9).
Ekvivalent med att
16^k $\equiv$ 8 (mod 9)<=>
7^k $\equiv$ 8 (mod 9) (*)

Nu,
7¹ $\equiv$ 7 (mod 9)
7² $\equiv$ 4 (mod 9)
7³ $\equiv$ 1 (mod 9)
och nu har vi nått 1, så denna sekvens kommer upprepa sig om och om igen.

Alltså kan högerledet aldrig bli 8, och (*) kan ej lösas. Att (*) ej kan lösas
implicerar att 2^m ej kan sluta på 6 och samtidigt ha siffersumma 8.

Lösning 3 (den snygga):

Antag att ett sådant tal finns. Notera att 2^k endast slutar på 6 om k är jämnt (t.o.m delbart med 4, men jämnt räcker).
Då har 2^k-1 siffersumma 7 och är inte delbart med 3. Men k=2n så
2²ⁿ-1=(2ⁿ-1)(2ⁿ+1).
Märk att talen 2ⁿ-1, 2ⁿ och 2ⁿ+1 är tre stycken på varandra följande, så något utav dessa måste vara delbar med 3. Men det kan inte vara 2ⁿ, eftersom det är en tvåpotens.
Någon av faktorerna i uttrycket är således delbar med 3 och vi får motsägelse.

Sabbad multiplikation

Rekommenderad från: 12 år

[kkratings]

På tavlan skrev matteläraren Adam en uträkning. Men precis innan lektionen skulle börja, så busade någon utav eleverna och bytte ut två siffror mot nya. Därefter stod det:

$4\cdot5\cdot4\cdot5\cdot4=2247$

Men vilka var siffrorna från början? Förklara hur du kommer fram till svaret.

Visa lösningen

Grisarna och kexen

Rekommenderad från: 13 år

[kkratings]

Vargen bjöd hem de tre små grisarna och Rödluvan för att titta på film. Efter att de var klara gick Vargen till köket, räknade alla kex och upptäckte att det saknades två. Men han har en stor balansvåg hemma som han kan använda. Hur kan med hjälp av två vägningar bestämma, vem som åt upp kexen? Alla kex väger lika mycket, alla grisar (i alla fall när de precis hade kommit till Vargen) också. Vargen vet även att Rödluvan bantar, så hon kunde max äta upp ett kex.

grisar

Visa lösningen

Överstrykning med sex streck

Rekommenderad från: 10 år

[kkratings]

Rita sex streck, så att alla 16 punkter på bilden blir överstrukna, utan att lyfta pennan från pappret och utan att strecken går längs med rutnätet.

vecka36

Visa lösningen

Dyra uträkningar

Rekommenderad från: 12 år

[kkratings]

Använd valutan euro, mynt och sedlar, för att beteckna talen 1, 2, 5 och 10. Med hjälp av dem och (gratis) parenteser och de fyra räknetecken (+, -, *, /) bilda ett uttryck, vars värde är 2009, genom att spendera så lite pengar som möjligt.

v26

Visa lösningen

Diskussion:

Notera att man aldrig ska använda 10:or i sitt uttryck, eftersom de kan ersättas med 2*5. På så sätt använder vi 7 euro i stället för 10 euro.

Ett snabbt sätt att komma upp i höga tal är att använda multiplikation. Vi försöker till exempel att faktorisera talet 2009 och skriva faktorer med hjälp av 1:or, 2:or och 5:or.

2009=41*49=41*7*7=(2*2*2*5+1)*(2+5)*(2+5)

Här använder vi 2+2+2+5+1+2+5+2+5=26 euro, vilket man skulle kunna tro är svaret. Men i uttrycket ovan förekommer faktorn 7, som är ”dyr”. Talet 8 skulle vara ”billigare”, bara kosta 6 euro (2*2*2=8). Vad händer om vi istället försöker faktorisera 2008 eller 2007?

Ett svar:

Genom att prova med olika tal kommer man fram till att det går att klara sig med 25 euro:

2009=2008+1=2*2*2*251+1=2*2*2*(5*5*5*2+1)+1

(2+2+2+5+5+5+2+1+1=25).

Jag har dock inget bevis för att det är det minsta möjliga antalet pengar man behöver använda.

Uppdatering:

Johan kom på ett sätt, där det går att klara sig med 24 euro. Tricket är att se 7:or som 2*(2+1)+1, det vill säga att de kostar bara 6 euro.

2009 = 49*41 = 7*7*41 = (2*(2+1)+1)*(2*(2+1)+1)*41 = (2*(2+1)+1)*(2*(2+1)+1)*(2*2*2*5+1)

2+2+1+1+2+2+1+1+2+2+2+5+1=24

Men det finns fortfarande inget bevis för att det skulle vara det minsta antalet pengar. Vi måste på något sätt bevisa att det aldrig går med 23 (eller hitta på ett exempel då det går).

Allmänna saker man kan säga är att multiplikation är det bästa sättet att få fram stora tal. Då är frågan vilka tal som är bäst att multiplicera, för att vi ska få så stort resultat som möjligt och spendera så lite pengar som möjligt. Vi struntar just nu i att uppgiften handlar om talet 2009.

1 är meningslöst att multiplicera med sig självt.

2-potenser är 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048 och så vidare. De kostar 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22 euro respektive.

3-potenser är 3, 9, 27, 81, 243, 729, 2187 och så vidare. De kostar 3, 6, 9, 12, 15, 18, 21 euro respektive.

4-potenser kostar lika mycket som 2-potenser, eftersom 4=2*2.

5-potenser är 5, 25, 125, 625, 3125 och så vidare. De kostar 5, 10, 15, 20, 25 euro respektive.

Här ser vi att 3-potenser egentligen är bäst bland de här, eftersom för 21 euro kan vi få 2187, medan ett mindre tal 2048 kräver för 2-potenser hela 22 euro. På liknande sätt kan vi jämföra med 5-potenser: 625 kostar 20 euro, men med 3-potenser kan vi få talet 729 med bara 18 euro.

Men vad händer om vi fortsätter med 6, 7, 8 euro? Där finns det bättre sätt att skriva just de talen än 1+1+…+1, nämligen

6 = 2*(2+1) fås med 5 euro,

7 = 2*(2+1)+1 fås med 6 euro (som förut),

8 = 2*2*2 fås med 6 euro (och i så fall blir lika bra som 2-potenser).

Vi kan se att i omskrivningar av de här talen använde vi faktiskt endast multiplikation med 2 och 3 och plussade på 1:or när det behövdes. Det tyder på att multiplikation med 2-3 är optimal. Det har att göra med att talet e = 2,718281828… ger snabbast tillväxt vid multiplikation med sig själv, men vi kan ju bara använda heltal.

Detta var egentligen Johans funderingar också, men vi har fortfarande inte kommit på något sätt att lösa gåtan helt. Alla ytterligare förslag är välkomna!

Ännu en uppdatering:

2009 = (2*3+1)*(2*4*4*3*3-1)
och talen 3 och 4 skrivs som 4=1+1+1+1, 3=1+1+1.

En följd av fyrhörningar

Rekommenderad från: 15 år

[kkratings]

Låt F₁ vara en godtycklig konvex fyrhörning. För k>1, F_k konstrueras genom att man skär F_k-1 i två delar längs en av dess diagonaler, vänder på en av delarna och sedan klistrar delarna samman längs samma diagonal. Bestäm det största möjliga antalet icke-kongruenta fyrhörningar i följden {F_k}.

Exempel:

För att förtydliga, en tillåten operation är följande:

lv25_1

Visa lösningen

Notera att om sidlängderna hos fyrhörningen är a, b, c, d, så finns exempel, där följden av fyrhörningar innehåller 6 icke-kongruenta: de med olika ordning på sidorna. Tag nämligenen fyrhörning med alla sidor olika, men som ändå påminner om en kvadrat (detta för att fyrhörningarna som bildas inte ska bli icke-konvexa). Men tillåtna operationer byt sedan plats på sidorna på alla möjliga sätt (trianglar med den gråa symbolen flippas):

l25

Ritningen är inte exakt, men vi kan se att alla olika sidordningar verkligen förekommer. Eftersom fyrhörningar kan roteras, valde vi fixera sidan med längden a, den kommer ändå alltid finnas.

Så nu är frågan varför det inte går att konstruera fler fyrhörningar? Notera att det finns en sak som aldrig förändras och det är summan av två motsatta vinklar i fyrhörningen. Vid varje flipp är det ett par av motsatta vinklar som inte ändras, således kommer vinkelsumman i det andra paret inte heller förändras.

Men notera också att sidlängderna kvarstår. Tag nu någon ordning på sidorna, vi skall nu bevisa att det går att bygga exakt en fyrhörning med den ordningen ur den ursprungliga. Utan inskränkning kan vi anta att sidordning är (medurs) a, b, c, d och a är den vänstra sidan.

Kalla vinkeln mellan a och d för x. Då är vinkeln mellan b och c också bestämd, nämligen S-x, där S var vinkelsumman av den ”nedre vänstra” och den ”övre högra” vinkeln. Men då har vi två trianglar, beståndsdelarna i fyrhörningen, som kan sättas ihop endast på ett sätt och det endast när de okända sidorna är lika (de ska bli en diagonal).

l25_2

De okända sidorna är lika endast för en vinkel x (den som det går att konstruera bilden för). Det beror på att om vinkeln minskas, så minskas också den motstående sidan. Men då ökar S-x och dess motstående sida, och då kan de sidorna inte längre vara lika. Samma sak händer om vinkeln x ökas.

På så sätt har vi uttömt alla fallen och visat att antalet olika fyrhörningar är 6, en för varje sidordning.

Turistens promenad

Rekommenderad från: 12 år

[kkratings]

En turist vill ta en promenad i Gamla Stan från busshållplatsen (punkt A) till sitt hotell (punkt B). Han vill ha en så lång rutt som möjligt. Han tycker att det är tråkigt att komma tillbaka till korsningar där han har varit förut, så det undviker han. Rita en så lång rutt som möjligt åt turisten och visa att det inte finns längre.

v24

Visa lösningen

Kortlekar som ligger snyggt

Rekommenderad från: 15 år

[kkratings]

Tag en vanlig kortlek med 52 kort. Säg att kortleken ligger snyggt, ifall varje par av kort där ena ligger på den andra antingen har samma färg eller samma valör, samma sak gäller för det översta och nedersta kort samt att spader ess ligger överst. Visa att antalet sätt att lägga kortleken snyggt är

(a) delbart med 12! (12 fakultet, det vill säga 12*11*10*9*8*7*6*5*4*3*2*1)

(b) delbart med 13! (13 fakultet)

spader_ess

Visa lösningen

(a) Det gäller alltså att hitta något villkor (som kan variera), som när det är uppfyllt ger upphov till exakt 12! olika fall. Det där låter lite luddigt om man inte har funderat på det, men här kommer det mer konkreta förklaringen.

Spader ess är fixt, det kan vi inte flytta på. Säg att vi har något snyggt sätt som kortleken är lagd på. Notera då att vi kan byta plats på alla treor och alla fyror i respektive färg (så hjärter tre och hjärter fyra byter plats osv.)

Men vi kan även byta plats på alla tvåor och kungar samtidigt. Vi kan egentligen byta plats på vilka valörer som helst så länge alla kort av den valören byts mot ett annat fixt valör och så länge essen inte flyttas (de får inte flyttas för spaderesset).

Eftersom man får byta plats på 12 valörer (man kan även byta fler än 2 valörer samtidigt, t.ex. tvåor byts mot treor, treor mot fyror och fyror mot tvåor), så finns 12! sådana byten. Därför är antalet snygga uppläggningar delbart med 12 fakultet.

”Villkoret” här var egentligen att vi fixerade vilken färg varje plats hade samt vilka platser som hade likadana valörer och alla essens platser var också bestämda. Det finns 12! sätt att nu placera ut de bestämda valörerna.

(b) Uppgiften kan ses på ett annat sätt. I fall det finns en 4×13-tabell, där raderna betecknar färger och kolonnerna betecknar valörer, så är antalet snygga sätt lika med antalet sätt som ett torn kan inuti tabellen så att den startar från säg vänstra övre hörnet, kommer till varje ruta en gång och sedan kommer tillbaka till sin egen plats. Kom ihåg att ett schacktorn kan gå lodrätt eller vågrätt godtyckligt många rutor.

Eftersom delen (a) är visat, räcker att bevisa att antalet sätt är delbart med 13. Klistra ihop tabellen längs de korta ändarna så att det bildas ett band med fyra rader. Om vi fixerar en rutt som börjar från spader ess så kan vi rotera bandet 12 steg så att det för varje steg bildas en ny rutt (som inte längre börjar med spader ess).

Vi visar att varje sådan falsk rutt kan göras om till en riktig och den kommer inte vara lika med den ursprungliga.

Varje falsk rutt går ändå igenom spader esset vid något tillfälle, och eftersom den kommer tillbaka till samma ruta som den startade ifrån så kan den lika gärna betraktas som en rutt som börjar i spader ess (som nu är tillåten).

Men varför är det inte lika med det ursprungliga? Då skulle rutten vid en viss rotation avbildas till sig sjäv. Betrakta då vilket som helst vågrätt drag (ett sådant måste finnas). Om vi gör rotationen 13 gånger så ser vi att alla rutor på den raden är startpunkter för vågräta drag (eftersom 13 är ett primtal). Men det kan inte vara möjligt, eftersom vi då inte kommer från den raden.

På så sätt delas rutter upp i grupper om 13 och alltså är antalet rutter delbart med 13!

Ödlornas läsning

Rekommenderad från: 13 år

[kkratings]

Vi människor läser vanligtvis från vänster till höger och uppifrån och ner. Ödlor är inte lika snabba på att läsa, men de kan göra det på fler olika sätt. Ödlan kan läsa en bokstav och sedan förflytta sig ett steg ner, upp, till höger eller till vänster för att fortsätta läsa.

På hur många sätt kan en ödla läsa ordet FJÄRIL här nedan?
val4

Visa lösningen

Diskussion:

Man kan förstås bara sätta igång och försöka räkna alla sätten. Det är en helt okej metod för att ta reda på svaret, men det finns ingen garanti på att man räknar rätt och inte glömmer någonting. Egentligen går uppgiften ut på att skapa just den garantin, att alla fall är medräknade. Det kallas att man gör systematisk undersökning.

Men det är krånglig att göra en direkt systematisk uppräkning. Det finns 11 stycken F att börja läsa på, redan där 11 fall som vi måste hålla koll på. Vid flera av F:en har vi två vägval, vi måste nämligen välja något J. Och så vidare … och det går förstås att komma fram till rätt svar men det blir mycket krångel.

Det underlättar att notera att bilden är symmetrisk. För varje F utom det längst upp finns ett motsvarande på andra sidan pyramiden. Det finns exakt lika många sätt att läsa FJÄRIL från de speglade F:n. Därför räcker det att räkna ut antalet sätt från de första 5 F:en och sedan multiplicera det med två och sedan addera ett sätt till (från det mittersta F:et går det att bara läsa neråt). Efter det kan man notera mer symmetri som underlättar beräkningar. Det slutar med att man bara måste räkna antalet sätt från de första tre F:en. Det blir totalt 1+5+10+10+5+1+5+10+10+5+1=63 sätt.

Vi kontrollerar detta på ett annat sätt.

Lösning:

Notera att antalet sätt att läsa ordet FJÄRIL är samma som antalet sätt att läsa ordet LIRÄJF (vi låter ödlan läsa baklänges). Och annorlunda formulerat, det är lika med antalet sätt att komma från bokstaven L till kanten av pyramiden, gående till nästa bokstav i ordet LIRÄJF varje gång.

Vi löser ett lite större problem. Nämligen, för varje ruta, sätt ut ett tal som berättar om hur många sätt det finns att ta sig till den rutan om man börjar i L. I början får vi följande bild, ty det finns bara ett sätt att komma till varje I från L:et:

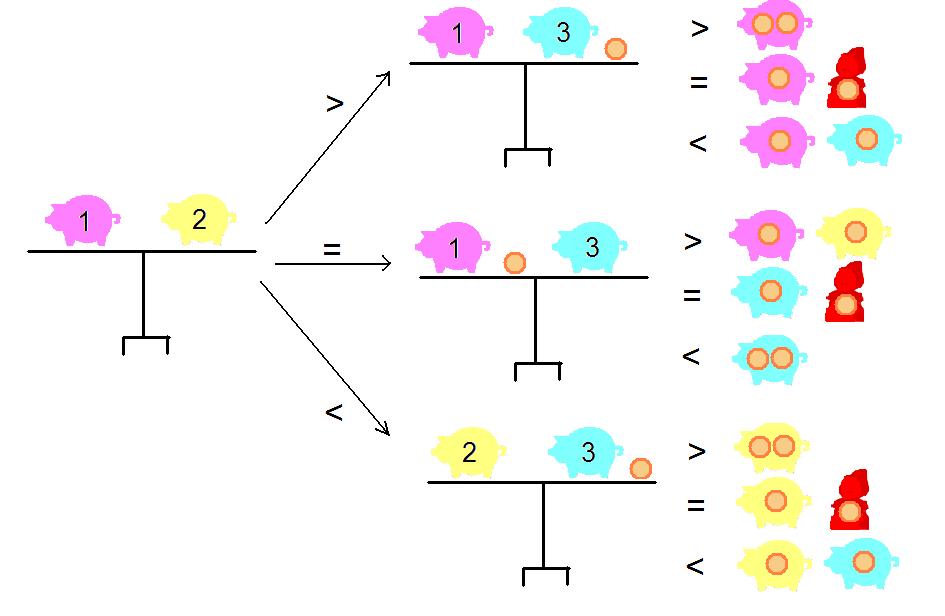
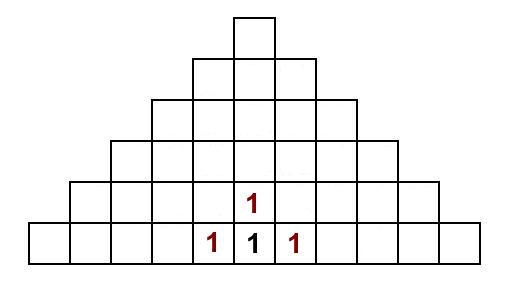lv22_1 Om vi nu ska forsätta vandra till R:en, så kan vi hamna i vissa R från två olika I. Därför ska antalet sätt adderas där och vi får totala antalet sätt att läsa LIR och sluta i ett specifikt R. Just här är det kanske inte så svårt att räkna dem sätten från början, men metoden blir mer användbar senare:

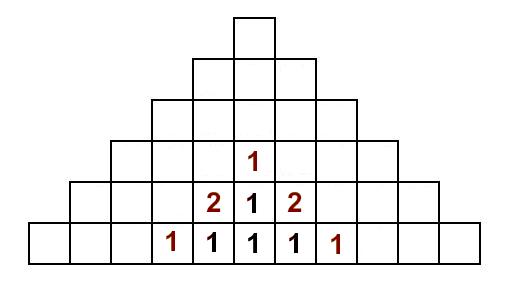lv22_2 Forsätt att fylla ut tabellen på det sättet. Varje nytt tal blir summan av talen som kommer ”precis innan”, till exempel på höger sida blir det summan av talet under och talet till vänster (om nu båda finns). Till slut fås tabellen:

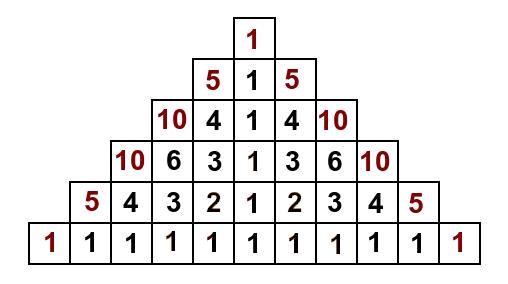lv22_3 Återigen, antalet sätt totalt att läsa ordet LIRÄJF är 1+5+10+10+5+1+5+10+10+5+1=63.

För dig som har orkat läsa så här långt kommer en extrafråga. Vad kommer svaret att vara om vi har ett längre ord istället för FJÄRIL? Låt säga att vi har en pyramid av samma sort, men ett ord som har n olika bokstäver.