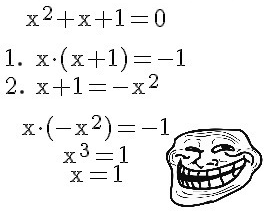
Etikett: andragradsekvation

Lösningen till problemet för de äldre vecka 46

Mattegåta

Visa att varje andragradspolynom kan skrivas som en summa av två andragradspolynom, vars diskriminanter är lika med 0.

Diskussion

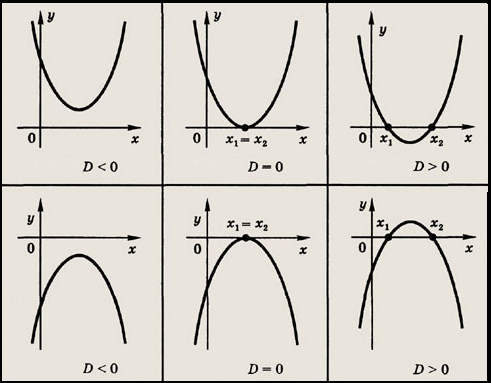
Vad var en diskriminant? För ett polynom Ax²+Bx+C är det talet B²-4AC.

Ifall diskriminanten är positiv, så har ekvationen Ax²+Bx+C=0 två reella rötter. Ifall den är negativ, så har ekvationen inga reella rötter. Om diskriminanten är 0, har ekvationen exakt en reell lösning.

Bilden illustrerar hur graden för ekvationen kan se ut i de olika fallen (D betecknar diskriminanten).

Nu när vi har koll på diskriminanten, kan uppgiften lösas grafiskt eller algebraiskt, vilken man nu föredrar. Nedan är en algebraisk lösning presenterad.

Lösning (av Benjamin Fayyazuddin-Ljungberg)

Låt P(x) vara polynomet vi vill skriva som summan av två andra polynom. Om P(x) = Q(x) + R(x) är kP(x) = kQ(x) + kR(x). Om Q(x) har diskriminant noll har kQ(x) också det. Därför kan vi utan inskränkning anta att P(x) har koefficienten 1 framför x²-termen.

Nu betraktar vi tre fall:

1) P(x) har diskriminant noll. Då har vi inga problem: P(x) = P(x)/2 + P(x)/2

2) P(x) har negativ diskriminant, det kan skrivas som (x-a)² + k² för någon konstant k. Låt z=x-a, så P(x) = z² + k². Då kan vi skriva P(x) som (z+k)²/2 + (z-k)²/2 = (x-a+k)²/2 + (x-a-k)²/2. Det är tydligt att de här polynomen bara har ett nollställe var, alltså är diskriminanten noll.

3) P(x) har positiv diskriminant, det kan skrivas som (x-a)² – k² för någon positiv konstant k. Låt z = x-a igen. Då är P(x) = z² – k². Vi skriver P(x) som 2(z-k/√2)² – (z-k√2)² = 2(x-a-k/√2)² – (x-a-k√2)². Dessa har också bara ett nollställe var, så de har diskriminant noll.

Matteproblem för de äldre vecka 46

Mattegåta

Visa att varje andragradspolynom kan skrivas som en summa av två andragradspolynom, vars diskriminanter är lika med 0.

Diskriminant

En diskriminant för ett andragradspolym Ax2+Bx+C är lika med

B2 – 4AC

Diskriminanter används för att bestämma ifall det finns lösningar för en given andragradsekvation och sedan beräkna dessa lösningar. Diskriminanten större än 0 ger två unika reella lösningar, lika med 0 ger en unik lösning, medan om diskriminanten är mindre än 0 så har ekvationen inga reella lösningar.

Lösningen till problemet för de äldre vecka 36

Mattegåta

Ekvationen x2+px+q=0 har bara heltalsrötter och man vet att både p och q är primtal. Hitta p och q.

Diskussion

Det hjälper att känna till faktorsatsen, som ger oss att polynomet kan uttryckas som (x-x1)(x-x2), där x1 och x2 är rötterna.

Vidare är det bra att känna till följande samband mellan koefficienterna (i vårt fall är det p och q) i en andragradare och dess rötter.

Viètes formler

Om ekvationen x2+px+q=0 har två rötter x1 och x2, så gäller:
x1 + x2 = -p
x1x2 = q.

Forsättningen på dessa tankar är ganska naturlig, som vi ser nedan.

Lösning (av Love Forsberg)

Låt a,b vara lösningarna till ekvationen. Då har vi att
(x-a)(x-b) = x2-(a+b)x+(ab) = x2+px+q=0, så
p = -(a+b), q = ab.

Men q = ab, q primtal och a,b heltal ger a eller b lika med ±1. Vi kan anta att a = ±1. Det följer också att b = ±q är ett primtal.

Vi noterar att primtal är positiva, så b har samma tecken som a.

Så p = -( ±1+b). Positiva a och b ger ett negativt p, vilket inte är tillåtet, så a och b är negativa.

p = -(-1+b) = -b+1, d.v.s. p är ett primtal som är ett högre än primtalet q. Det finns bara en möjlighet, p = 3, q = 2 (a = -1, b = -2).

Matteproblem för de äldre vecka 36

Mattegåta

Ekvationen x2+px+q=0 har bara heltalsrötter och man vet att både p och q är primtal. Hitta p och q.

© 2009-2024 Mattebloggen