Rekommenderad från: 13 år
[kkratings]
Vi människor läser vanligtvis från vänster till höger och uppifrån och ner. Ödlor är inte lika snabba på att läsa, men de kan göra det på fler olika sätt. Ödlan kan läsa en bokstav och sedan förflytta sig ett steg ner, upp, till höger eller till vänster för att fortsätta läsa.
På hur många sätt kan en ödla läsa ordet FJÄRIL här nedan?

Diskussion:
Man kan förstås bara sätta igång och försöka räkna alla sätten. Det är en helt okej metod för att ta reda på svaret, men det finns ingen garanti på att man räknar rätt och inte glömmer någonting. Egentligen går uppgiften ut på att skapa just den garantin, att alla fall är medräknade. Det kallas att man gör systematisk undersökning.
Men det är krånglig att göra en direkt systematisk uppräkning. Det finns 11 stycken F att börja läsa på, redan där 11 fall som vi måste hålla koll på. Vid flera av F:en har vi två vägval, vi måste nämligen välja något J. Och så vidare … och det går förstås att komma fram till rätt svar men det blir mycket krångel.
Det underlättar att notera att bilden är symmetrisk. För varje F utom det längst upp finns ett motsvarande på andra sidan pyramiden. Det finns exakt lika många sätt att läsa FJÄRIL från de speglade F:n. Därför räcker det att räkna ut antalet sätt från de första 5 F:en och sedan multiplicera det med två och sedan addera ett sätt till (från det mittersta F:et går det att bara läsa neråt). Efter det kan man notera mer symmetri som underlättar beräkningar. Det slutar med att man bara måste räkna antalet sätt från de första tre F:en. Det blir totalt 1+5+10+10+5+1+5+10+10+5+1=63 sätt.
Vi kontrollerar detta på ett annat sätt.
Lösning:
Notera att antalet sätt att läsa ordet FJÄRIL är samma som antalet sätt att läsa ordet LIRÄJF (vi låter ödlan läsa baklänges). Och annorlunda formulerat, det är lika med antalet sätt att komma från bokstaven L till kanten av pyramiden, gående till nästa bokstav i ordet LIRÄJF varje gång.
Vi löser ett lite större problem. Nämligen, för varje ruta, sätt ut ett tal som berättar om hur många sätt det finns att ta sig till den rutan om man börjar i L. I början får vi följande bild, ty det finns bara ett sätt att komma till varje I från L:et:
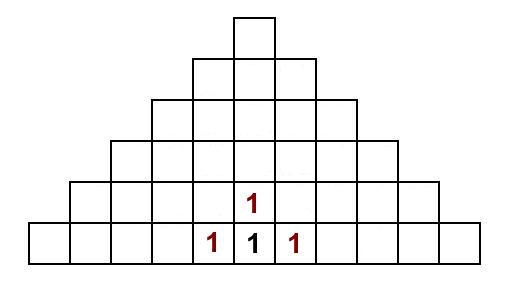 Om vi nu ska forsätta vandra till R:en, så kan vi hamna i vissa R från två olika I. Därför ska antalet sätt adderas där och vi får totala antalet sätt att läsa LIR och sluta i ett specifikt R. Just här är det kanske inte så svårt att räkna dem sätten från början, men metoden blir mer användbar senare:
Om vi nu ska forsätta vandra till R:en, så kan vi hamna i vissa R från två olika I. Därför ska antalet sätt adderas där och vi får totala antalet sätt att läsa LIR och sluta i ett specifikt R. Just här är det kanske inte så svårt att räkna dem sätten från början, men metoden blir mer användbar senare:
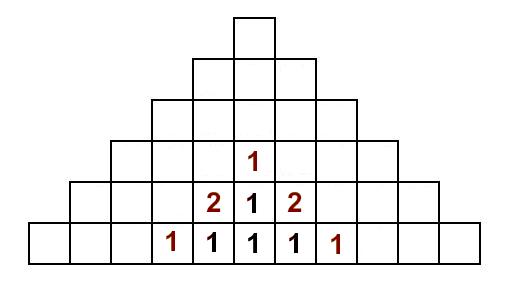 Forsätt att fylla ut tabellen på det sättet. Varje nytt tal blir summan av talen som kommer ”precis innan”, till exempel på höger sida blir det summan av talet under och talet till vänster (om nu båda finns). Till slut fås tabellen:
Forsätt att fylla ut tabellen på det sättet. Varje nytt tal blir summan av talen som kommer ”precis innan”, till exempel på höger sida blir det summan av talet under och talet till vänster (om nu båda finns). Till slut fås tabellen:
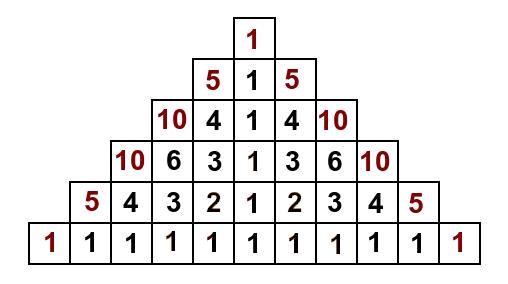 Återigen, antalet sätt totalt att läsa ordet LIRÄJF är 1+5+10+10+5+1+5+10+10+5+1=63.
Återigen, antalet sätt totalt att läsa ordet LIRÄJF är 1+5+10+10+5+1+5+10+10+5+1=63.
För dig som har orkat läsa så här långt kommer en extrafråga. Vad kommer svaret att vara om vi har ett längre ord istället för FJÄRIL? Låt säga att vi har en pyramid av samma sort, men ett ord som har n olika bokstäver.
