Året var 1997. Det var då jag började ha matematiska framgångar och blev därmed skickad på en resa till den stora staden Moskva. Där skulle jag och andra 6:or och 7:or tävla i problemlösning. Som jag minns det gick det hyfsat ok för mig, men ett problem kunde inte de flesta deltagarna lösa:
En familj kommer fram till en bro mitt i natten. Pappan kan gå över bron på 1 minut, mamman – på 2 minuter, barnet – på 5 minuter och mormorn – på 10 minuter. De har bara en lykta. Bron håller bara för två personer åt gången. Hur ska alla ta sig över till andra sidan på 17 minuter? (Om två personer går över samtidigt, går båda lika snabbt som den långsammaste av dem. Man får inte gå på bron utan lyktan. Man får inte lysa långt bortifrån. De får inte bära varandra.)
Ännu tidigare i min matematiska karriär hörde jag talas om problemet om Bonden och hans ägodelar:
En man ska ta sig över en å i en roddbåt. Han medför en varg, en get och ett kålhuvud. Han kan inte ta med sig mer än en av ägodelarna åt gången. Vargen kan inte lämnas ensam med geten och geten kan inte lämnas ensam med kålhuvudet. Hur skall mannen bära sig åt för att klara övergången?
Kanske vet du lösningen, kanske inte. Det är roliga är att numera finns problemet i form av ett spel!
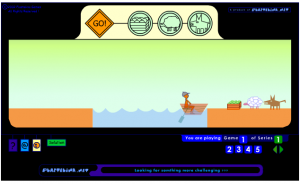
Prova även att få över missionärer och kannibalen till andra sidan. Båten rymmer två, men blir det fler kannibaler än missionärer på någon sida, blir missionärerna uppätna.
Och till slut kan du prova att få över familjen med lyktan på andra sidan. Den här familjen är dock lite större än i problemet i början, och har lite annorlunda tider. Men illustrationen till problemet är suverän.
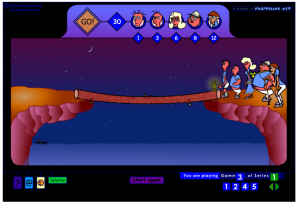
Alla ni som tyckte om problemen om familjerna, kan försöka lösa det generella fallet. Vilket är den minsta tiden att ta alla över till andra sidan, om familjen har 
medlemmar som tar sig över på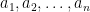 
minuter där 
?
