Figur i tre delar
Lösningen till problemet för de yngre vecka 45
Mattegåta
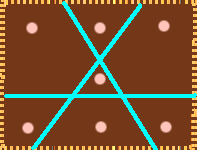
En chokladtårta är rektangelformad och sju personer ska dela på den. På tårtan finns 7 marsipanrosor:
Hur kan man dela tårtan i sju delar så att det finns en ros i varje del, om man bara får skära tårtan tre gånger och skärningarna måste vara raka linjer? Observera att delarna inte behöver vara lika stora.
Diskussion
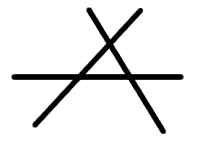
Om det till en början inte verkar gå med tre linjer, tänk på vad tre linjer kan bilda för konfigurationer vid sidan av tårtan. Tre linjer som inte korsar varandra i en och samma punkt och som inte är parallella bildar en triangel och sex oändliga delar om de ritas på ett oändligt plan.
Sju är det maximala antalet delar, så linjerna på tårtan ska bilda någon liknande figur (det ska vara en ros i varje del).
Ett annat sätt att komma fram till svaret är att rita en linje i taget. Om man tänker från slutet, måste varje del på tårtan innehålla högst två rosor innan sista linjen ritas (så att den eventuellt skär på dessa delar). På samma sätt, måste varje del innehålla högst fyra rosor innan den andra linjen ritas. Så den första linjen som ritas måste dela tårtan i två delar: en med tre rosor och en med fyra.
Lösning (av Nicklas Yttergren)
Så här till exempel:
