När någon ställer frågan ”Vad är matematik för dig?” svarar jag ibland ”Att tänka.” Det kan tolkas som ett luddigt svar eller att jag kanske tror att matematik är viktigare än allt annat. Men så är inte riktigt fallet och jag ska försöka visa vad jag menar med hjälp av ett exempel.
Problem
Framför dig är en rektangel. Du sätter ut två punkter inuti rektangeln och förbinder alla de med alla hörnen, till exempel så som bilden visar. Vilken area är störst: den svarta eller den grå?
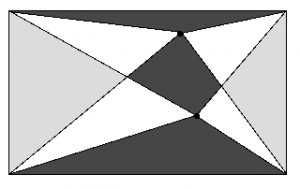
Försök att tänka ut svaret utan att använda dig av några som helst variabler eller uträkningar. Svårt, eller hur?
Låt mig presentera ett tankesätt som gör den här uppgiften väldigt lätt istället.
Fläckar
Föreställ dig ett vitt A4-papper och ett litet barn som målar med blått och gult akvarellfärg. Hon målar abstrakt konst, det vill säga det gula blir någon slags oregelbunden fläck, det blå likaså. Barnet målar inte så noggrant, på vissa ställen täcker fläckarna över varandra och på så sätt bildas det gröna områden.

När bilden blev färdig visade det sig att den sammanlagda arean av de två fläckarna är lika stor som arean av hela pappret. Visa att den gröna arean är lika stor som den vita arean.
Beviset får vi genom att ställa den enkla frågan: ”Hur mycket area behövs för att komplettera den blå, den gula arean och den gröna arean till arean av hela pappret?” Visuellt behövs bara den vita arean, för att det är den som är kvar. Men om vi tänker på att fläckarna tillsammans skulle utgöra arean av hela pappret så ser vi att det saknas en till grön area för det. Det gula och det gröna är nämligen en hel fläck, men det blåa saknar just det gröna för att bli en hel fläck (eller tvärtom). Eftersom det saknas precis lika mycket när vi tänker på två olika sätt så måste den gröna arean och den vita arean vara lika stora.
Vi löste uppgiften utan att använda oss av X eller någon annan variabel. Egentligen resonerade vi precis som men gör med ekvationer, men med ord istället. Ibland kan det vara lättare, ibland svårare, men här är det mer intuitivt tycker jag, speciellt om man ska förklara lösningen för någon annan!
Tänka geometri
Vad har uppgiften med abstrakta fläckar med riktig geometri att göra? Låt oss bevisa att den svarta och den grå arean är lika i följande figur:
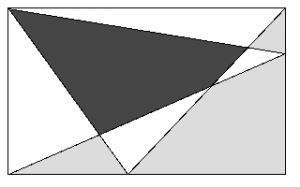
Vi kan även tänka att regelbundna former utgör fläckar. I följande figur kan vi göra om färgerna till gult, blått, grönt och vitt. Ser du de två fläckarna? Och att det gröna är precis skärningen de emellan och det vita är precis den delen de inte täcker?
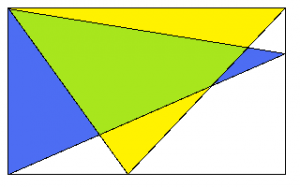
För att visa att den gröna arean är lika stor som den vita behöver vi bara förklara varför trianglarna tillsammans utgör arean av hela rektangeln. Varje sådan triangelarea utgör hälften av rektangelns area (för detta kan vi t.ex. använda areaformlerna, för rektangeln är det basen gånger höjden, men för triangeln är det precis hälften av det). Alltså utgör summan av areorna på trianglar exakt hela rektangelns area. Klart!
Kan du identifiera fläckarna i den ursprungliga uppgiften och lösa den utan att räkna alls? Kom ihåg att fläckarna kan ha godtycklig form och behöver inte ens vara sammanhängande!
Uppgifter utan räkning
Detta är vad jag menar med att ”tänka matte” istället för att ”räkna matte”, vilket är det uttrycket de flesta använder (eftersom de oftast gör just det senare, men inte det första).
Siffror och variabler är bra att införa när de behövs, men det finns fördelar med att försöka klara sig utan dem. Det kan vara tillräckligt för att lösa ganska komplicerade problem, som till exempel uppgiften i början. När vi presenterar idéer, uppgifter och lösningar av den typen för barn blir de oftast inte rädda, då det bara finns ord och bilder. Barn har inte fördomar mot resonemang med ord, till skillnad mot variabelräkning. Där har fördomarna oftast utvecklas efter att barnet tvingats jobba på ett visst sätt med ekvationer (dock kan de tyvärr ha fördomar mot geometri också). Så passa på och sätt dina elever (och dig själv) i situationer, där du inte har någon aning om hur man löser problemet. Du får då vara kreativ och kommer förmodligen att komma på ett lättare sätt att hantera uppgiften än vad någon annan skulle ha berättat för dig.
