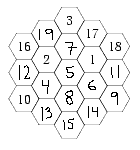
Hexagonen (1 poäng).
Fyll i rutorna i ”hexagonen” nedan med heltalen från 1 till 19, så att summan av talen i varje kolonn och i varje diagonal blir densamma. Varje tal får utnyttjas exakt en gång, och vissa tal är redan på sin plats:
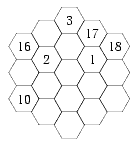
Siffersumman (3 poäng). Hitta alla tal som är 12 gånger större än sin siffersumma.
Visa lösningar
Siffersumman (Toomas lösning):
Vi börjar med att göra en definition och att visa ett lemma och därefter bestämma alla tal med den givna egenskapen.
Definition: Låt högstagradsiffran mena den siffra vars tiopotensfaktor har högst grad multiplicerat med den givna tiopotensen och beteckna detta med a*10^n.
Lemma: Alla tal med 4 siffror eller fler är större än 12 gånger deras siffersumma.
Bevis:
Antag att talet har t siffror. För att maximera siffersumman maximerar vi varje ingående term. Vi kan då notera att var sådan högst kan vara 9, varav vi ser att den maximerade siffersumman fås av den tecknade produkten 9t. Siffersumman multiplicerat med 12 blir då 12*9t=108t.
Denna produkt blir alltid mindre än talet, ty det alltid blir mindre en högstagradsiffran, då t≥4. För att minimera värdet av högstagradssiffran sätter vi a=1 och får att högstagradssiffran är 10^n. Vi kan också se att n=t-1 och få utsagan 108t<10^(t-1) för t≥4. Detta kan inses av att för varje t≥4 ökar det vänstra uttrycket med en faktor av 108, då det högra ökar med en faktor av åtminstone 1000.
HSB.
Vi ser nu att talet antingen är en-, två eller tresiffrigt.
Om det är ensiffrigt och siffran är a, får vi ekvationen
12a=a, som har lösningen a=0.
Om talet är tvåsiffrigt och siffrorna är a och b, får vi ekvationen
12(a+b)=10a+b
och finner att
a=-(11b)/2.
Då a och b måste vara positiva har denna ekvation inga lösningar.
Om talet är tresiffrigt med siffrorna a, b och c, får vi ekvationen
12(a+b+c)=100a+10b+c
varav vi finner att
88a=2b+11c
Om a≥2 får vi
2b+11c≥88*2=176
För att maximera vänster led sätter vi b=c=9, och får
2b+11c=2*9+11*9=117≥176
vilket är en motsägelse. Alltså gäller att a<2.
Då a är hundratalssiffran måste a≠0, vilket med den föregående utsagan ger att a=1. Insatt i ekvationen blir detta
88=2b+11c.
Om vi gör några algebraiska omskrivningar får vi att
11(8-c)=2b.
Detta betyder att b är en multipel av 11. Vi har dock att 0≤b≤9, vari den enda multipeln av 11 är 0, vilket betyder att b=0. Sätter vi detta i ekvationen får vi
88=11c
vilket förstås ger
c=8
Det enda tresiffriga talen med den givna egenskapen är alltså 108.