Uttrycket (3 poäng).
Man utvecklade uttrycket (x+y)^n med hjälp av binomialsatsen. Den andra termen i summan blev lika med 240, den tredje blev lika med 720 och den fjärde blev lika med 1080. Hitta x, y och n.
Ön (7 poäng).
a) På en platt cirkelformad ö finns 4 hamnar (i den ordningen): 1, 2, 3 och 4. Mellan dem finns vägar där det kan finnas korsningar, det vill säga punkter där vägarna möts, korsas eller grenas. På alla sträckor är trafiken enkelriktad, på så sätt att man aldrig kan komma tillbaka till en hamn eller korsning om man startar därifrån. Låt fij beteckna antalet vägar som går från hamn i till hamn j.
Visa olikheten f14f23≥f13f24
b)
Visa att om det finns 6 hamnar (1, 2, 3, 4, 5, 6 i den ordningen) så gäller
f16f25f34+f15f24f36+f14f26f35≥f16f24f35+f15f26f34+f14f25f36
Visa lösningar
Uttrycket (Toomas lösning, kompletterad):
Vi har alltså en utveckling av ett binom (x+y) upphöjt i ett tal n enligt binomialsatsen sådant att den andra termen är lika 240, den tredje 720 och den fjärde lika 1080.
Vi förnimmer oss att binomialsatsen kan skrivas
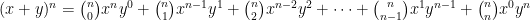
Detta innebär att om vi ersätter den retoriska notationen i problemtexten med symbolisk algebra får ekvationssytemet
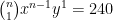


som förstås kan förenklas till

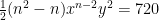
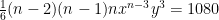
Dividera den andra ekvationen med den första, samt den tredje ekvationen med den andra:


Subtrahera den andra ekvationen från den första

och gör en ersättning i en av ekvationerna för att få n:

Nu kan vi göra ersätta n med 5 i den första ursprungliga ekvationen:

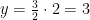
Den enda lösningen är alltså n=5, x=2 och y=3.
Ön (Skäggets lösning, något modifierad):
a) Vi noterar att f13*f24 kan ses som antalet sätt man kan gå från 1 till 3 och sedan från 2 till 4, och att f14*f23 är antalet sätt man kan gå från 1 till 4 och sedan från 2 till 3.
En väg från 1 till 3 delar vår ö i två delar, med 2 och 4 på olika sidor. Således måste en väg från 2 till 4 korsa varje väg från 1 till 3 vid minst en punkt.
Tag en godtycklig väg som går från 1 till 3 (kalla den A) och sedan magiskt fortsätter vid 2 och går till 4 (via en väg B). A och B måste korsa varann i någon punkt X (vi kan exempelvis välja den första korsningen på A).
Antag att vi börjar från 1 och följer A tills vi når X. Sedan fortsätter vi längs väg B tills vi når 4. Sedan hamnar vi på något magiskt vis i 2 och följer B tills vi når X, och följer sedan A till 3.
Vi ser att för varje sammansättning A och B får vi en väg från 1 till 4 och sedan 2 till 3. Detta ger upphov till en funktion som uppenbart är injektiv (två vägar måste ju ha identiska vägsegment såväl före som efter X för att ett vägskifte vid X ska ge samma resultat, och då är de samma väg).
Således har vi en injektiv funktion från mängden av vägar 1-3-2-4 (med magiskt hopp från 3 till 2) och mängden av vägar 1-4-2-3 (med magiskt hopp från 4 till 2). Dessas mängders storlekar är som vi noterat f13*f24 respektive f14*f23, och således har vi visat olikheten i fråga.
b)Vi ser att vänsterledet kan ses som unionen av alla vägar 1-6-2-5-3-4 och 1-5-2-4-3-6 och 1-4-2-6-3-5 (med magiska hopp), sådana vägar kallar vi udda. Högerledet kan ses unionen av alla vägar 1-6-2-4-3-5 och 1-5-2-6-3-4 och 1-4-2-5-3-6, sådana vägar kallar vi jämna. Om två hamnar med nummer 4, 5 eller 6 byter plats i en väg, byter vägen paritet.
Tag en väg 1-x-2-y-3-z, där {x,y,z} är en permutation av {4,5,6}. Om delsträckorna skär varandra någonstans, kalla skärningspunkten närmast 1 för M (det vill säga skärningspunkten som kommer först på sträckan 1-x om den sträckar korsar andra, annars skärningspunkten närmast 2 på sträckan 2-y). Byt plats på vägsluten efter punkten M, precis som i punkt a). (Om alla delsträckorna går genom M bestämmer vi en regel om att alltid byta plats på vägsluten av desträckorna 1-i och 2-j.)
Om man byter två stycken vägslut byter vägen paritet. På så sätt har vi bestämt en bijektion mellan udda och jämna vägar som har korsningar. Varje väg som inte har korsningar är dessutom en udda väg av typ 1-6-2-5-3-4. Därför finns det minst lika många udda vägar som jämna. Av det följer olikheten.
