Anders och Filip spelar ett spel. De turas om att göra drag: Anders får sätta ett kryss i en tom ruta och Filip får sätta en ring i en tom ruta. Dock får inte två kryss hamna bredvid varandra och inte heller två ringar. Spelaren, som inte kan göra ett drag när det är hans tur, förlorar.
Anders gör det första draget. Vem har ett vinnarstrategi, det vill säga vem kan alltid vinna oavsett hur motståndaren spelar?
Observera att svaret kan bero på talen n, som säger hur lång remsan är.
För det första är n=1 ett specialfall. Det finns bara ett sätt som spelet kan gå till på, nämligen att Anders sätter kryss och Filip kan inte göra något drag längre och därför förlorar.
Men för alla andra storlekar på remsan så vinner Filip. Det roliga är att hans första drag måste vara speciellt, men efteråt kan han spela hur som helst så länge hans drag är tillåtna och ändå alltid vinna, oavsett hur Anders spelar.
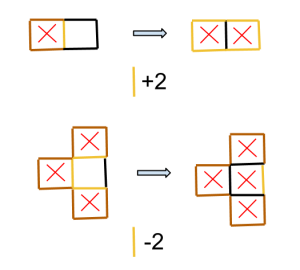
Anders börjar med att sätta kryss någonstans. Det kan vara på remsans ände eller så kan det vara någonstans däremellan. I vilket fall som helst kan Filip sätta ring i en av remsans ändrutor:
 eller
eller
 De fortsätter spela under tillåtna regler (aldrig två kryss eller två ringar bredvid varandra). Låt oss säga nu att Filip på något sätt lyckas förlora. Det betyder att han i en viss situation har ingenstans att sätta sin ring och de har precis varit Anders tur.
De fortsätter spela under tillåtna regler (aldrig två kryss eller två ringar bredvid varandra). Låt oss säga nu att Filip på något sätt lyckas förlora. Det betyder att han i en viss situation har ingenstans att sätta sin ring och de har precis varit Anders tur.
Eftersom Anders började och det precis har varit hans tur, så har han gjort ett fler drag än Filip, det vill säga det finns ett fler kryss än ringar på remsan.
Men notera att i den här situationen måste två utsatta kryss ha en ring mellan dem. För att två kryss kan inte vara bredvid varandra, och hade det bara funnits tomma rutor mellan dem, så skulle Filip ha haft ett möjligt drag.
Alltså finns det minst en ring mellan varje par av kryss. Om vi börjar räkna upp symboler från kanten där Filip gjorde sitt första drag (första ringen) kommer vi se: ring, kanske fler ringar, kryss, ringar, kryss, ringar, kryss, … , slutar med kryss eller ring. (Här betyder ”ringar” att det kan vara exakt en ring också). Schematiskt exempel: OXOOOXOOXOOOXOOOXOOX.
Men då ser vi att varje kryss har minst en ring strax till vänster om sig. Det betyder att antalet kryss kan i den här situationen inte vara fler än antalet ringar. Vårt antagande om att Filip inte kunde göra drag var fel, därmen kommer Filip alltid att kunna göra drag efter att Anders har gjort sitt. Alltså är det Anders som först inte kommer kunna göra drag och förlorar för n>1.


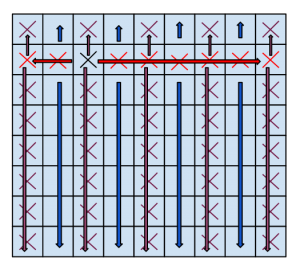
 eller
eller De fortsätter spela under tillåtna regler (aldrig två kryss eller två ringar bredvid varandra). Låt oss säga nu att Filip på något sätt lyckas förlora. Det betyder att han i en viss situation har ingenstans att sätta sin ring och de har precis varit Anders tur.
De fortsätter spela under tillåtna regler (aldrig två kryss eller två ringar bredvid varandra). Låt oss säga nu att Filip på något sätt lyckas förlora. Det betyder att han i en viss situation har ingenstans att sätta sin ring och de har precis varit Anders tur.