Mattegåta
Fem fotbollslag spelade en turnering, där alla lag mötte alla en gång. För en vinst tilldelades 3 poäng, för oavgjort 1 poäng och för förlust gavs inga poäng.
Fyra av lagen fick 1, 2, 5 och 7 poäng respektive. Hur många poäng fick det femte laget?
Diskussion
I alla för mig blir det lättare att lösa turneringsproblem, om man ritar en graf eller en tabell över resultaten.
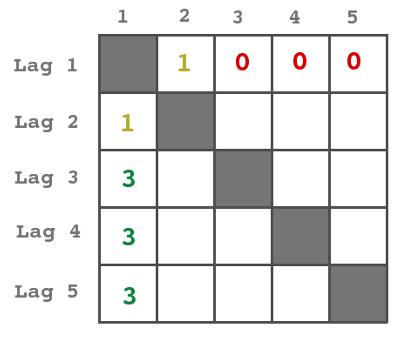
Till exempel vet vi att ett av lagen fick 1 poäng, då kan man utan inskränkning anta att det är Lag 1. Då ser deras rad i tabellen ut som nedan.
Kolonnen är på sätt och vis motsatsen, alla förluster byts mot vinster (Lag 3, 4 och 5 vann ju mot Lag 1). Problemet går ut på att ta reda på sista radens poängsumma!
Lösning (av Nicklas Yttergren, kompletterad)
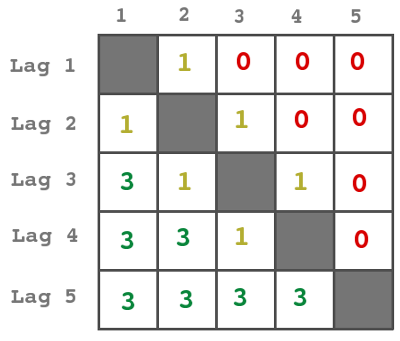
Observera hur många matcher har förlorats och hur många vunnits, de måste ha varit lika många. Totalt var det 7 förluster och 3 vinster utan att man räknat med med det femte laget (det ser man på poängen 1=1+0+0+0, 2=1+1+0+0, 5=3+1+1+0, 7=3+3+1+0).
Då måste det femte laget vunnit alla sina matcher, eftersom de spelade fyra och det är precis så många vinster som saknas. Därför fick de 12 poäng.