Kulor i olika färger
[kkratings]
Tre personer A, B och C räknade antalet julgranskulor av olika färger på granen. Var och en kunde skilja på två av färgerna, men de andra två kunde hen förväxla: En av dem förväxlade ibland röd och rosa, en annan kunde förväxla rosa och beige, och den tredje av dem kunde förväxla beige och gul. De sammanställde olika antal som de kom fram till i en tabell. Hur många kulor av varje färg fanns i granen på riktigt?
| Röd | Rosa | Beige | Gul | |
| A | 2 | 5 | 7 | 9 |
| B | 2 | 4 | 9 | 8 |
| C | 4 | 2 | 8 | 9 |
Trassel (tangles)
Aktiviteten trassel
Rekommenderas för: gymnasieet, universitetet (eller i förenklad form för högstadiet)
Materiel: två stora rep eller sladdar (gärna av olika färger), en ogenomskinlig plastpåse
Tid: 45 minuter
Antalet deltagare: 4 + publik
Aktiviteten ”trassel” kommer från matematikern och pusselkonstruktören Johan Conway och har genomförts i Sverige på bland annat Sonja Kovalevsky-dagarna. Den passar att genomföra på en matematiklektion om bråkräkning/gruppteori eller som en extra matematikaktivitet.
Man börjar med att fyra elever ställer sig som hörnen på en kvadrat inför resten av klassen. Var och en av dem tar tag i var sin ände av ett rep så att repen hänger parallella med hur publiken sitter. Under experimentet får de aldrig släppa sin ände.
Så här ser det ut uppifrån (Positionerna närmast klassen är D och C):
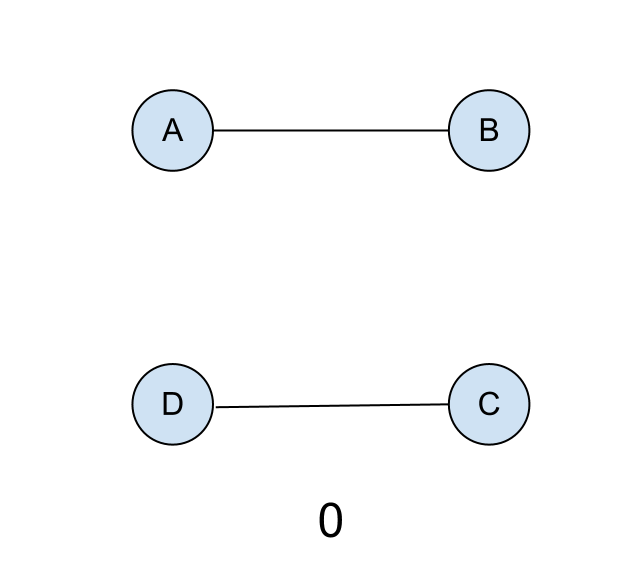
Nu kommer de fyra personerna utföra en slags dans och trassla till repen samtidigt. Varje trassel (tangle) repen bildar kommer att ha ett motsvarande tal. Från början, när repen är parallella mot varandra och mot klassen, motsvarar det talet 0.
Det första tillåtna danssteget är att vrida om repen runt varandra. Och inte på vilket sätt som helst, utan det måste göras av personerna som står på positionerna B och C. Dessa två personer byter plats med varandra och B är den som lyfter sin repände, som C går under för att komma till sin nya position.
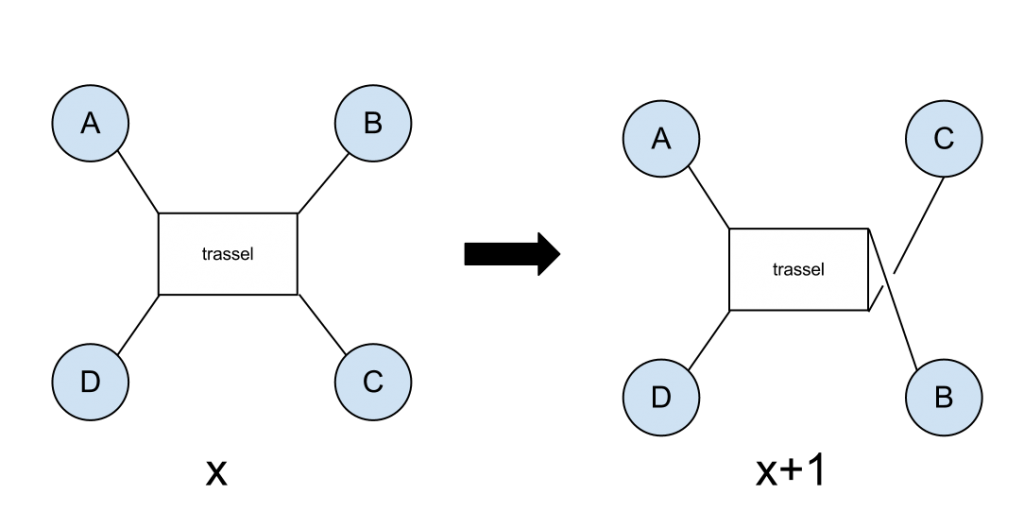
Att vrida om trasslet på det här sättet kommer att öka talet med 1. Så en omvridning ger ett trassel med värdet 1, medan en till omvridning ger talet 2 osv.
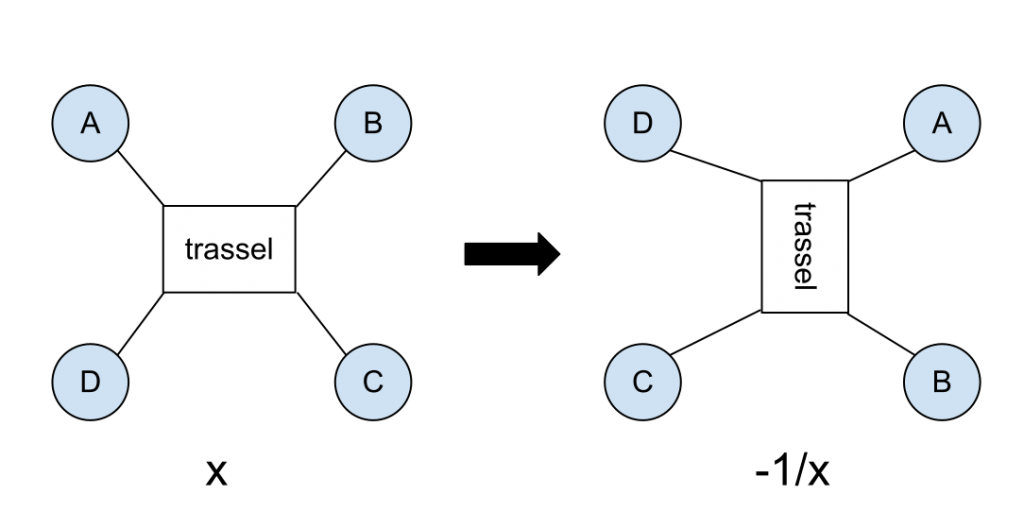
Det andra tillåtna danssteget är att rotera medurs. Person A går till position B, person B går till position C och så vidare.
Att rotera trasslet kommer också att förändra talet. Men hur? Om elevera har hållit på med funktioner och algebra tidigare kan man låta dem att lista ur svaret. Annars kan man helt enkelt säga att talet x omvandlas till talet -1/x vid en sådan rotation. Notera t.ex. att två rotationer i rad inte gör någon skillnad på trasslet, vilket är klart för trassel som består av några omvridningar:
n -> -1/n -> -(1/(-1/n)) = n
När alla har förstått reglerna kan man be eleverna att uföra några danssteg (börja med att först
vrida om), samtidigt som man räknar på talet som ska motsvara trasslet. Om man från början gör dansstegen: vrida om, vrida om, rotera, vrida om, vrida om, vrida om, rotera, vrida om så kommer man till talet:
0 -> 1 -> 2 -> -1/2 -> 1/2 -> 3/2 -> 5/2 -> -2/5 -> 3/5
Hur ska man lösa upp detta trassel om man bara tillåts att göra dansstegen ovan? Publiken får lösa denna uppgift genom att försöka räkna ut hur man ska göra med bråket 3/5 för att det ska bli 0, om man bara tillåts addera 1 och ta den negativa inversen. Man kan ju inte göra dansstegen ”baklänges”, eftersom steget ”att vrida runt åt andra hållet” inte finns.
När någon har kommit på dansstegsföljden kan man testa dansen och se att knuten verkligen löses upp.
Det här kan man göra med andra tal. Ju svårare trasslet är, desto roligare blir det att se det lösas upp. När repen är tilltrasslade, kan man knyta några plastpåsar runt dem, så att trasslet inte syns och sedan utföra dansstegen som eventuellt ska lösa upp trasslet. När talet på tavlan är 0 kan man knyta upp påsarna och se att allt blir som i början, bara man drar i repen!
Fler frågor att diskutera på avancerad nivå:
– Vad händer om man roterar först? Vad är talet -1/0 och vad har det för egenskaper? Ska trasslet -1/0 förändras om man vrider om det?
– Hitta inversen till att vrida om. Det vill säga, om man startar från ett trassel och sedan vrider om en gång, vad för danssteg skall man göra för att komma tillbaka till starttrasslet?
Fler frågor för att grupper:
– Om man börjar från 0, hur kommer man till ett specifikt trassel, t.ex. -3?
– Hut kommer man snabbast ner till 0 från ett specifikt trassel? Här kan eleverna tävla om vem som kan hitta på kortaste dansstegsekvensen när trasslet är ett relativt avancerat bråktal.
Mer om aktiviteten kan du läsa i Conways text (tangles börjar på sida 10) conway.pdf, samt Tom Davis text med utförlig diskussion och beskrivning av aktiviteten. tangle.pdf.
Tack till Johan Björklund för tipset!
Sabbad multiplikation
Rekommenderad från: 12 år
[kkratings]
På tavlan skrev matteläraren Adam en uträkning. Men precis innan lektionen skulle börja, så busade någon utav eleverna och bytte ut två siffror mot nya. Därefter stod det:
Men vilka var siffrorna från början? Förklara hur du kommer fram till svaret.
Att sätta händerna i degen
I den stora boken ”Algebra” av Grillet liknar författaren viss matematikinlärning med att knåda deg. Att lära sig vissa saker går bara om man själv försöker härleda eller använda dem. Till exempel matrisräkning kan man inte utantill om man inte multiplicerat en enda matris.
Jag håller fullt med om detta. Var själv väldigt priviligerad om att gå i den hårda ryska skolan och räkna 20 polynom, ekvationer och uttryck om dagen. Samma sak med multiplikation och division i de tidigare skolåren. Detta kommer till en användning i vardagen, då jag inte alltid har dator/miniräknare med mig, men oftast tillgång till papper & penna eller tavla & krita.
Jaja, det är kanske ingen som bryr sig om att kunna räkna fort nuförtiden, varken tal eller andragradsekvationer, men människor vill kunna göra det (utan miniräknare). Speciellt studenter. Och enda vägen att lära sig är hårda vägen.
Vad är bästa sättet att få eleverna att göra 20 ganska likadana uppgifter?
Om motivationen är ”klara provet” eller ”klara tentan” är det plötsligt en väldigt tråkig sak för dem att göra, för att man ”måste”. Det sättet som gjorde det roligt för mig i lågstadiet i alla fall var att jag tävlade mot min bänkkamrat. Oavsett om det var rysk grammatik eller matte, så tävlade vi om vem som gjorde uppgifterna snabbast på lektionen. Långt ifrån alla är tävlingsinriktade förstås och alla har olika tempo. Dessutom var det inte läraren som gjorde det roligt för oss, utan det var vi själva.
Som lärare har jag inte vågat säga åt eleverna att utföra det här repetativa uppdraget. Det har Thomas Erlandsson däremot gjort till mina nya elever och jag kan säga att det funkar hur bra som helst. Han sa åt dem att räkna ett hundratal uppgifter från boken och det gör de också. När allt kommer omkring, är inte uppgifterna så djävulkst tråkiga.
När det gäller matriser och linjära avbildningar, så har jag gjort en stencil som börjar enkelt och testar färdigheter, men sedan blir allt svårare. Jag delade ut den på lektion 9 i kursen ”Linjär algebra och geometri I” och man fick sitta med var sin stencil och komma så långt man kunde. Notera att samtidigt som att man gör standarduträkningar, smyger ovanliga uppgifter in och de får upptäcka lite matematik själva. Jag kan stolt skryta om att eleverna inte märkte när lektionstiden var ute, för de var så inne i stencilen. Här är den och stort tack går till min vän Djalal, som fixade kaninbilderna. (Bäst är att läsa den i utskriven version för sidorna på slutet är bilder som hör till tidiga uppgifter.)
Har ni några tips på att göra tråkig räkning rolig?
