Korstal 2014
Fyll i precis som ett vanligt korsord (men endast med siffror). Obs! Inga tal börjar med noll.

Vågrätt:
1. Delbart med 9
4. Valören på en svensk sedel
5. Alla siffror i talet är likadana
7. Ett kubtal delbar med lodrätt 3
9. Ett tal bestående av siffror som är kvadrattal, där alla sådana siffror förekommer
11. Vågrätt 1 plus vågrätt 5 minus lodrätt 1
Lodrätt:
1. Antalet positiva tvåsiffriga tal
2. Ett palindromårtal i det förflutna
3. En delare till lodrätt 2
4. Vågrätt 1 minus vågrätt 5
5. Vågrätt 1 gånger vågrätt 5
6. Vågrätt 9 plus lodrätt 5
8. En tvåpotens minus lodrätt 1
10. Delbart med lodrätt 3
Ett kvadrattal är kvadrat av ett heltal. Ett kubtal är kub (tredjepotens) av ett heltal. Ett palindromtal är ett tal som ser likadant ut fram- som baklänges. En tvåpotens är 2 multiplicerat med sig själv några gånger (även 1 och 2 räknas som tvåpotenser). Med delbart med N menas att det går att jämnt dela med talet N. Med delare till N menas att N går att dela jämnt på det talet.
Andra träffen med Matteklubben, åk 2-4
Minsta eleverna som går i Matteklubben är de i åk 2-4. Du kan också läsa om den första träffen med gruppen här på bloggen.
På den andra träffen kom färre elever, men de var precis lagom många för att vi skulle hinna prata med alla. Barn i årskurser upp till 4 är mycket aktiva och berättar gärna sina lösningar. Vi var 6 lärare och 29 elever. Ju yngre barnen är, desto lägre måste elev/lärare-kvoten vara, enligt min erfarenhet ungefär 4-5 för yngre barn och 6 (absolut högst 7) för äldre barn.
Blandade problem
Lektionen började med att eleverna satt två och två och löste blandade problem, precis som vi brukar göra med de äldre grupperna. Under varje uppgift står vanliga dialoger som jag och de andra lärarna hade med eleverna.
1. Andreas skrev upp talen i ordning tills siffran 2 skrevs upp 10 gånger. Han började med talet 1. Vilket tal slutade Andreas på?
Elev: 92, för att han började på 2, sedan är det 12, sedan 22, 32, 42, 52, 62, 72, 82, 92. Tio tal ger tio tvåor!
alternativt:
Elev: 82, för att han började på 2, sedan är det 12, sedan 22 (två tvåor), 32, 42, 52, 62, 72, 82. Tio tvåor!
Lärare: Måste tvåorna som skrivits upp alltid vara den sista siffran? (Pekar på 22.) Här är det en tvåa som talet börjar med. Finns det inte fler sådana tal?
Elev (efter en liten tankestund): Ja, just det, det är så på 20, 21, 22… Räknar snabbt fram till talet 26 (eller 27 om den andra tvåan i 22 glöms bort).
2. Så fort deltagarna ankom till Matteklubben bildades det en lång kö till fikat. Precis bakom Adam står Linda, precis bakom Linda står Hjalmar. Om man räknar från köns början, står Hjalmar som nummer tjugo. Om man räknar från slutet, står Adam som nummer trettio. Hur många personer står i kön till fikat?
Elever: Är svaret 46?
Lärare: Kanske, berätta hur ni tänkte!
Elever: Om Adam är nummer 30 från slutet, så är det 27 personer bakom Hjalmar i kön. På samma sätt är det 17 framför Adam. Mellan Adam och Hjalmar är det 2 (personer). Tillsammans blir det 27 + 17 + 2 = 46.
(Det fanns också andra förklaringar till 46 som jag måste erkänna att jag inte riktigt förstod. Det var inte helt lätt att fånga upp felet i resonemang där man är slarvig med att räkna med/inte räkna med personer som står på ändarna)
Lärare: Vilka personer har vi räknat in och vilka har vi inte räknat in? Har vi räknat någon två gånger?
alternativt:
Lärare: Om det är 27 personer bakom Hjalmar, hur många är resten? Alltså från nummer 1 till Hjalmar som är nummer 20? (Det var inte helt självklarat för vissa barn att det var 20.)
3. Med hjälp av siffrorna 0, 5 och 9 bilda det största möjliga samt det minsta möjliga tresiffriga talet. Siffrorna i talet måste alla vara olika.
Elev: Det är 905 och 059.
Lärare: Men 059 räknas inte som tresiffrigt.
Elev: Aha, då är det 509.
4. Tre ekorrar hittade 90 nötter. De delade upp nötterna på så sätt att den äldsta ekorren fick 10 nötter mer än mellanekorren och så att den yngsta ekorren fick 10 nötter mindre än mellanekorren. Hur många nötter fick varje ekorre?

Elever: Vi tänkte först att alla skulle få lika många nötter, 30 stycken. Men sedan skulle den minsta ge 10 till den största, så det blev 40, 30, 20.
alternativt:
Elever: Vi testade med 30, 20, 10, men då blev det för lite. Det saknas 30 nötter. Då lade vi på 10 till varje ekorre.
5. På en idrottslektion ställde sig hela klassen på en rad. Först skulle var sjunde barn göra två steg fram. Sedan skulle var tredje barn (av de som var kvar i ledet) göra ett steg fram, och till sist skulle var femte barn (av de som var kvar) göra ett steg bakåt. Hur många går i klassen om 15 barn stod kvar på sina platser i slutändan?
Elever: Är svaret 30?
Lärare: Låt oss kontrollera!
(Vi kontrollerar för 30 genom att rita upp 30 pinnar/saker, stryker dem en i taget och ser att det fungerar.
Lärare: Finns det fler svar?
Några av elevparen blev klara med uppgifterna snabbt, och då fick de lösa ett par extra uppgifter från träffen med åk 5-6.
Sedan var det dags att presentera lösningarna på tavlan. Många av eleverna/grupperna var ivriga att få gå fram. För att fler skulle få komma fram fick de göra det två och två. De som var bekväma med att prata inför gruppen fick presentera lösningen, de andra agera som stöd (ibland turades båda om att prata).
Eleverna hade snygga (förfinade efter diskussion med läraren) lösningar på uppgifterna. Till exempel, på uppgift 1 skrev de bara upp talen från 1 till 26 som innehöll siffran 2 (eftersom de andra var irrelevanta). På uppgift 2 ritade eleverna upp hur de tänkte, vilket nästan påminde om Venn-diagram, man kunde lätt följa deras resonemang. Efter att uppgift 3 hade presenterats frågade jag hur man i allmänhet bildade största möjliga och minsta möjliga tal med en given mängd siffror. Barnen kunde svara på det utan problem, även om vissa först tänkte att 0 kunde stå på första plats i ett tal (även någon enstaka lärare trodde att det var ok).
Fixering vid svar
Det jag har märkt både under diskussionerna med eleverna och i sättet de presenterar lösningarna på tavlan är att de lägger stor vikt vid att formulera svaret. De tycker att det absolut ska stå ”Svar:” någonstans på pappret (eller när man presenterar på tavlan). Eller så glömmer de ibland bort att skriva det, men när de är färdiga med lösningen kommer de ihåg att avsluta med ”Svar: 30 elever” till exempel.
Detta läggs förstås vikt på i skolan, för att läraren lätt ska få en överblick över om uppgiften gjorts rätt eller inte. Under Matteklubben försöker jag skifta fokus från svar till själva lösningar. På frågan ”Är __ rätt svar” svarar jag alltid ”Hur tänkte ni?” för att visa att det är tanken och inte vad man räknade ihop på slutet, som räknas. Extra roligt är det att ta med uppgifter där det finns flera svar på lektionerna. Då förstår eleverna bättre när läraren ställer frågorna ”Finns det fler svar på uppgiften? Varför/varför inte?”. De börjar undersöka mer för att själva försäkra sig om att de verkligen har betraktat alla möjligheter. Vi straffar inte elev för att hen har gissat sig fram till ett svar, för det är också en slags strategi (som kan ge rätt svar), men vi försöker säga att det inte räknas som en fullständig lösning förrän man är säker på att det inte finns fler svar.
Det var det som hände vid diskussionen av uppgift 5, då vi kom fram till att det finns ett ytterligare svar än det som presenterades på tavlan. Men därefter kunde vi också förklara varför antalet elever i raden inte kunde bli större eller mindre.
Experiment med utvikningar
Nu fick eleverna vara i gruppen om 3-5 och undersöka olika utvikningar. Varje grupp fick en sax och en linjal, samt papper för att klippa ut och testa utvikningar. Till uppgift 2 tog jag med en Rubiks kub som fick stå framme på katedern. Om man ville testa sin utvikning, fick man alltså komma fram och göra det. Till uppgift 3 tog jag med några tändsticksaskar (därav måtten) som eleverna också kunde testa utvikningar på. Men det var nästan ingen som hade kommit så långt.
Eleverna var lite mer trötta vid det här laget och hade svårigheter med att läsa igenom och skilja på de olika uppgifterna. Jag sade till många att de skulle komma på egna utvikningar, men då läste ju inte eleverna uppgift 2 så noga (eftersom de antog att de redan hade fått det förklarat) och många missade att sidan skulle vara 6 cm. Inte för att det gör särskilt mycket. Men nästa gång ska jag ha tydligare gräns mellan uppgifterna, kanske till och med ge ut dem en i taget.
1. Vilka av figurerna på bilden kan vecklas ihop till en kub?
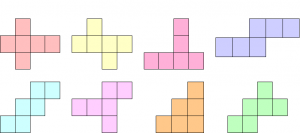
Vissa elever föreställde sig hur det skulle bli i huvudet (och då gjordes såklart också några fel) och kunde utesluta eller godkänna några former. De flesta klippte ut och testade med papper när de var osäkra. Den metoden fungerade perfekt. Några av eleverna sade att de redan hade gjort liknande uppgifter tidigare på lågstadiet och då kan man ju bara glädjas åt att de verkar ha haft roligt då i skolan. Jag hoppas dock att alltid lära ut något extra med uppgifterna på Matteklubben, så som diskussionen nedan.
2. Hitta på en annan utvikning till en kub och tillverka den. Kubens sidor är 6 cm långa. Klipp ut din utvikning och testa den på kuben.
Några grupper gjorde en egen utvikning i rätt storlek, några gjorde mindre utvikningar. Det bästa med stora utvikningar var att vi kunde testa dem på Rubiks kub och alla kunde se att det passade. Många grupper hittade den utvikningen, som är lik den första, fast man flyttar två av rutorna (så att formen ser ut som bokstaven ”T”). Då uppmanade jag dem att hitta på en till.
3. Kom på en utvikning till ett rätblock som är 1,5 cm hög, 4 cm bred och 5,5 cm lång. Klipp ut och testa utvikningen!
Under tiden någon klipper ut utvikningen, försök att komma på fler annorlunda utvikningar till samma rätblock. Du behöver inte rita dem snyggt, bara på ett ungefär.
En grupp tillverkade utvikningen och vi testade den sedan på tändsticksasken. Möjligen hade de flesta grupper inte hunnit komma så långt, då vi inte hade så mycket tid för det här momentet.
Diskussion
Vi ritade upp alla utvikningar (inklusive de falska) från uppgift 1 på tavlan och gick igenom dem en och en och klassen fick skandera ”ja” eller ”nej” som svar på frågan huruvida de var möjliga eller inte. De flesta hade alla rätt. Vi markerade även vilka rutor som var tvungna att överlappa ifall man skulle klippa ut figuren och försöka vika en kub utav den.
Sedan var det dags för grupperna att lämna in utvikningar som de själva hade kommit på. Det blev tre annorlunda former totalt och de ritade vi upp (och visade upp de stora). Jag berättade att det totalt finns 11 utvikningar så om man ville, kunde man försöka hitta de 2 vi saknade. Här bifogar jag en bild över alla ifall man är nyfiken:
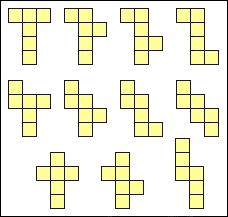
Sedan visade vi upp utvikningen för ett rätblock som en grupp hade gjort (som var korrekt och inspirerad av standardformen (”plus”) på kubutvikningen). Då ställde vi en fråga till barnen: ”Tror ni att finns fler utvikningar för en rätblock än för en kub eller färre?”. ”Färre!” skanderade barnen. De tänkte att det var svårare att rita upp en utvikning för ett rätblock (svårare att passa in sidor), alltså måste det finnas färre sådana.
Då försökte vi diskutera fram till att om en utvikning för ett rätblock kan göras av en kub-form, skulle en inte då kunna göras av andra kubformer också? Långsamt blev barnen mer och mer övertygade om detta. ”Lika många, lika många!” skrek de då.
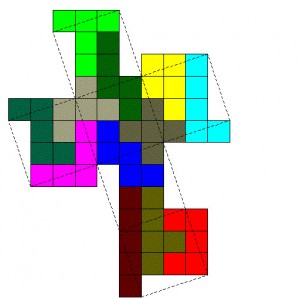
Sedan ritade jag och en annan lärare upp flera olika former för rätblock som egentligen hade samma underliggande standardutvikningsform för kuben. Vi kunde variera den på minst tre olika sätt, genom att välja form och riktning på ”sidoflärparna” (det finns ju tre olika rektangelytor). Då började fler och fler barn långsamt bli övertygade om att de faktiskt fanns fler former för rätblock (som inte är kuber) än för kuber. Jag avslöjade att det fanns ungefär 50 utvikningar för rätblock. ”Och vi ska hitta de alla!” sade en elev med uppspärrade ögon. Kul tänkt, men matte ska ju helst inte var plågsamt :) Så det behövde de förstår inte göra, men jag bifogar de ändå här:

Hemuppgift
Det fanns extrauppgifter på bladet som de flesta inte hann komma till. Därför fick de ta dem med sig hem och tänka över dem i lugn och ro. Hemuppgiften är förstås frivillig.
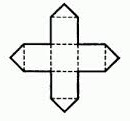
Konstig nog går även den här formen att vika ihop till kub (testa hemma)!
Kan följande former också vikas ihop till kuber?
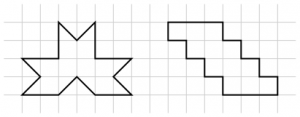
Jag berättade om vad den första uppgiften gick ut på (att man skulle klippa ut den delen som var i färg). Barnen blev väldigt förvånade över att det var en utvikning (”hur ska man vika ihop den då?”). Då tipsade jag om att det fanns en ritning över kuben, som var sned och att man kunde ta den som grund. Då förstod en av eleverna att de bitarna som stack ut passade ihop precis med det som saknades på rutorna bredvid. Får se om någon tar sig an de sista tre formerna och lyckas vika ihop dem till en kub. Det är inte särskilt lätt ens för vuxna!
Utvärdering
De 29 eleverna som kom till lektion kände sig motiverade och trivdes bra (förutom för en elev som var där för första gången och inte hade roligt), så gruppen är rolig att arbeta med. Nivån var till och med enkel för många, så det gäller att ha ett förråd med svårare uppgifter, ifall någon blir klar väldigt fort (t.ex. uppgifter från åk 5-6 kan passa). Barnen blev fortfarande trötta mot slutet, men eftersom uppgifterna var mer tillgängliga än första gången, orkade nästan alla jobba hela vägen fram.
En annan lärare påpekade, efter att han på en rast hjälpt en elev att fatta lösningen på uppgiften om fikakön, att det viktigaste med matten är inte att fatta, utan att försöka fatta. Kloka ord tycker jag, Har man nyfikenheten och ihärdigheten, så kan man komma hur långt som helst!
Andra träffen med Matteklubben, åk 5-6
Matteklubben är Uppsala kommuns satsning på begåvade elever i matematik. Jag har äran att förbereda aktiviteterna som vi håller på med och vara en av lärarna. Du kan kolla upp var vi gjorde på första träffen innan du läser vidare.
36 elever och 6 lärare
Denna gång var det 36 elever som var närvarande, vilket är närmare ett lagom antal än förra gångens 41. Vi var sex stycken lärare och jag tror att vi räckte till det mesta av tiden. Om uppgifterna hade varit för lätta, så skulle vi inte ha så mycket att diskutera med barnen, förutom att de skulle berätta hur de tänkte (och vi skulle förmodligen inte hinna lyssna på allas lösningar). Och om uppgifterna hade varit för svåra så skulle vi inte lärarna ha så mycket att göra annat än att tipsa eleverna om hur de kan tänka. Det är lagom nivå på uppgifter om eleverna löser några, tänker fel på några andra (så att de lär sig något nytt!) och kanske har svårt för att lösa de allra svåraste problemen på egen hand, så att de börjar utbyta idéer med varandra. Vi kunde även lyssna på några elever som inte hittade någon att samarbeta med (eller inte ville samarbeta, vi tvingande ingen att vara i grupp, bara uppmanade). Jag hann i alla fall själv att prata med nästan alla grupper åtminstone en gång, vilket borde betyda att de flesta grupper har hunnit bolla var och en av sin idéer med åtminstone någon av lärarna.
Hemuppgiften
Vi började träffen genom att gå igenom (den frivilliga) läxan. Några av eleverna kom ihåg den och hade jobbat med den hemma, de flesta hade säkert glömt bort den (eller inte jobbat på den). Därför försökte jag föra diskussionen på ett sådant sätt att även de som var helt nya för Matteklubben kunde hänga med lite grann. Vi diskuterade i bara 10 minuter för att de som inte hade fördjupat sig i uppgiften inte skulle bli uttråkade.
Uppgiften som handlar om konkreta tal (5 pärlor, si och så många av varje färg) kunde alla lösa om de försökte. Det handlar om att rita upp och inte glömma något fall. Det fanns ändå flera tolkningar på uppgiften där det fick vara alla möjliga antal svarta pärlor av fem. Några tolkade uppgiften som att armbanden inte fick vara helt svarta eller helt vita. Det gjorde inte så mycket, eftersom man bara behöver lägga till 2 till svaret om dessa armband skulle räknas.
En annan oväntad kuriosa uppstod när jag ritade upp de olika armbanden på den svarta tavlan med en vit krita. Jag tyckte att de pärlorna jag fyllde i var ”svarta”, men många barnen tyckte att dessa var ”vita” (eftersom det verkligen var den färgen de fick). Detta resulterade i ett par intressanta matematiska poänger. Dels att man själv får välja (definiera) vad man kallar för ”svart” och ”vitt”. Och dels att man kan se att det finns lika många armband med 3 svarta och 2 vita pärlor som armband med 2 svarta och 3 vita pärlor, eftersom man kan välja vilken färg man ser som ”svart”.
Vi gick igenom de andra fallen tillsammans: alla svarta, alla vita, 4 svarta + en vit, 4 vita + en svart. Totalt blev det 8 olika armband, om man räknar armband som fås via vridning som samma. Som jag sett av hur eleverna löste läxan, så betraktade de även spegelvända armband som samma (vilket inte var tanken med uppgiften), men detta spelar ingen roll förrän man börjar räkna armband med 7 pärlor.
Sista delen av uppgiften var en öppen fråga. Det vara bara 2-3 elever som hade jobbat på det hemma och berättat det för mig. Sambandet för ett godtyckligt antal pärlor är väldigt svårt. Så det var inte tanken att eleverna skulle lösa det, men de kanske kunde upptäcka vissa mönster. Om man inte räknar spegelvända armband som samma, så går uppgiften att lösa med Burnsides Lemma i det generella fallet (vilket är universitetsmatte), och i fall då antalet pärlor i armbandet är ett primtal (p) så är antalet armband lika med
Så till exempel för talet 5 blir svaret:
Försök att lista ut var svaret kommer ifrån (tips: 2:an står för antalet färger). Obs! Uppgiften är bara till för de elever som tycker allting annat är jättelätt.
I varianten där spegelvända armband räknas som samma vet jag inte hur man löser uppgiften generellt.
Blandade uppgifter
Sedan löste eleverna blandade uppgiften i ungefär 40 minuter. Vissa satt själva och vissa jobbade i grupper om 2-3. Individuellt arbete är mycket givande, men vi hinner inte jobba med var och en så mycket då antalet elever är så stort. De som räcker upp handen fick dock hjälp snabbt och om de som var villiga att diskutera kunde de få en givande dialog. Exempel på några typiska dialoger skriver jag under varje uppgift.
Om du undrar över lösningen på någon uppgift, så är det bara att fråga i kommentarerna.
Första uppgiften tog längst tid så den diskuterade jag absolut mest med eleverna.
1. a) Matilda har två leksakskuber med bokstäver på sidorna. Totalt finns det 12 olika bokstäver. Hur många ord på två bokstäver kan Matilda bilda?
Lärare: Obs! Låtsasord är också ord i den här uppgiften.
Elever: Får ett ord bestå av två likadana bokstäver?
Lärare: Javisst!
Elever: Det är 6 bokstäver på första kuben och 6 bokstäver på andra. Totalt blir det 6 x 6 = 36 ord.
Lärare: Men måste alltid den första kuben (till exempel den med bokstäverna ABCDEF) alltid stå först? Kan inte den stå på andra platsen?
Elever: Just det, då blir svaret dubbelt så stort!
Elever: Den första bokstaven kan man välja på 12 sätt. Den andra på 11 sätt. Totalt blir det 12 x 11 = 132 ord.
Lärare: Men det är bara en sida man kan välja per kub. Två bokstäver på samma kub bildar inte ett ord.
Elever: Aha, då är det 12 x 6.
Elev: Blir svaret 66?
Lärare: Kanske, hur fick du svaret?
Eleven berättar hur hen tänkte och det visar sig att hen hade tänkt rätt, men räknat fel.
Lärare: Du tänkte rätt!
Det var en del elever som inte noterade att alla de 12 bokstäverna var olika, och därmed snarare löste b)-uppgiften.
1. b) David fick däremot två likadana kuber. Hur många ord på två bokstäver kan han bilda?
Elever: Samma svar som i a), 72 sätt.
Lärare: Låtsas som att vi bara har två bokstäver per kub, A och B på första kuben och likadant på den andra. Vilka ord kan man bygga? T.ex. AA är ett ord.
Elever: Man kan också bygga BB, AB och BA.
Lärare: Så svaret blir…?
Elever: 4 ord.
Lärare: Men om vi skulle tänka som i första uppgiften skulle svaret bli 8 ord. Vad är felet?
2. Det är mörkt i rummet och du vet var det finns en låda med 7 röda och 5 blå pennor. Hur många pennor måste du dra på måfå för att vara säker på att ha minst 2 röda och 3 blå pennor när du sedan kommer ut ur rummet?
Elev: Om man drar 10 pennor, så kan man få 7 röda, men då får man ändå 3 blå.
Lärare: Varför räcker det inte med 9 pennor?
Elev: Man skulle kunna få 7 röda och 2 blå.
3. Vilja räknade fingrarna på sin högra hand: första var tummen, andra – pekfingret, tredje – långfingret, fjärde – ringfingret, femte – lillfingret, sjätte – ringfingret igen, sjunde – långfingret, åttonde – pekfingret, nionde – tummen, tionde – pekfingret och så vidare. Vilket finger blir nummer 2014?
Elever: Vi räknade att pekfingret blir nummer 10, ringfingret nummer 20, ringfingret nummer 30, pekfingret nummer 40, pekfingret nummer 50 och så vidare. Vi räknade ut vad finger nummer 2000 blir och sedan var det bara räkna 14 till. Och det blev ringfingret.
Lärare: Ok, coolt sätt att lösa uppgiften på!
Elev: Nummer 2010 blir pekfingret och sedan spelar det faktiskt ingen roll åt vilket håll man går, om 4 fingrar är det ändå ringfingret.
Lärare: Ja, intressant att man inte behöver bry sig om håll.
4. Siffrorna 1 till 9 fyller kvadraten som det syns på den vänstra bilden. Man får gå på kvadratens rutor, men aldrig tillbaka till en ruta man varit på förut, och man måste alltid gå till en angränsande ruta.
Emilia gick längs med pilen som syns på den högra bilden. Hon skrev ner siffrorna som hon gick på i ordning och fick talet 84937561. Rita en annan väg, som ger ett större tal (ju större tal, desto bättre).
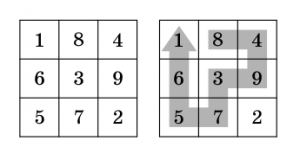
Elev: Man måste börja på ett hörn, annars kan man inte gå igenom alla rutor…
Lärare: Kan man inte börja i mitten?
Elev: Men det är ändå lägre!
Lärare: Ja, förvisso.
Elev: Då börjar man med största siffran i hörnet, 5, och sedan går till 7, för 7 är större än 6. Sen går man till 2, för om man går till 3, så kan man inte komma till 2 senare.
Lärare: Kan inte man sluta i 2?
Elev: Jo, kanske, vänta nu lite!…
5. Gustav tänkte på tre tal, men berättade inte vilka tal det var. Däremot sade han vilka olika summor som två av talen kunde bilda: Det var 23, 25 och 28. Vilka tal tänkte Gustav på?
Elev: Jag testade och hittade talet 10, 13 och 15.
Lärare: Kan det ha varit några andra tal han tänkte på som också passar?
Elev: Jag vet inte, jag provade mig fram bara.
Redovisning
Eleverna fick komma fram till tavlan och redovisa sina lösningar, om de ville. Jag försökte att inte lägga ner så mycket tid på det, för då skulle det bli för lite tid kvar till temat. Det vill säga, vi lyssnade på bara en elevlösning per problem.
Intressanta frågor som dök upp (och som jag själv delvis svarade på för att ge exempel på fullständigt resonemang) var:
Problem 2.
– Varför är man säker på att 10 pennor är tillräckligt?
– Man vet att man får 5 röda och 5 blå, eller 6 röda och 4 blå, eller 7 röda och 3 blå. Det är tillräckligt i varje fall.
Problem 4.
– Hur vet man att man måste börja i ett hörn eller mitten med pilen?
– Om man målar kvadraten schackrutigt, så att 5 rutor blir målade (och 4 omålade), så kan man inte starta i en omålad ruta, eftersom man måste hela tiden växla för varje steg:
omålad – målad – omålad – målad – omålad – målad – omålad – målad, vilket gör att man inte kommer att kunna gå på alla 9 rutor.
Problem 5.
(Det har var egentligen ett förtydligande av en annan elevs resonemang).
– Hur vet man att det inte finns något annat svar än 10, 13, 15?
– Om man ökar något tal till exempel, så måste man sänka båda andra och då skulle inte den tredje summan stämma.
Det här resonemanget är inte vattentät kom jag på i efterhand. Om man ökar ett visst tal, så kanske är man inte säker på att det ingår exakt i samma två summor som förut. Till exempel, om vi ökar 15 till 16, så är det inte säkert att 16 ingår i summan 28, utan kanske i de andra två summorna. Det gör att vi inte lika säkert kan förutspå hur de andra två talen måste förändras.
Forskning om area och omkrets
Med dagens tema fick eleverna jobba i grupper om ungefär 4. Det tog inte så lång tid, då frågorna var lite lättare och öppnare än de blandade problemen. De som blev klara fort fick pappret med individuella uppgifter.
Efter ungefär 20 minuter (tror jag) diskuterade vi elevernas förslag på tavlan. Jag skriver under varje uppgift vad vi tog upp i klassdiskussionen.
Figurerna i de här tre uppgifterna får bara ritas längs med rutornas gränser. Inga halva rutor tillåtna det vill säga.
1. Rita så många figurer som möjligt med omkretsen 8 (rutlängder). Vad har de olika figurerna för areor?
Eleverna ritade de två figurerna som består av tre rutor (”pinnen” och ”vinkelhaken”) och en som består av fyra rutor (”fyrkanten” eller ”kvadraten”). En grupp tänkte utanför lådan och hittade på en figur med area 0 (sträckan med längd 4) och med area 2 (två rutor som hänger ihop ett hörn). Jag berättade att figurer som den med arean 0 kallas för ”degenererade figurer” och man bestämmer själv ifall de ska räknas som figurer eller inte (därefter hade vi en omröstning i klassen och majoriteten tyckte inte att de räknades som figurer).
2. Rita så många figurer som möjligt med arean 8 (rutor). Vad har de olika figurerna för omkrets?
Eleverna fick jättemånga olika figurer här, så att de inte ens orkade rita upp alla (jag frågade sedan vilken grupp som hade ritat flest figurer). Omkretsarna var 16, 14, 9, 18.
En av lärarna frågade hur en elev hade fått omkretsen 9. Då ritade eleven upp en kvadrat med ett hål i (också nytänkande!). Omkretsen tyckte eleven var det som var utanpå (hålets omkrets räknades inte med). Men då blev det inte 9, utan 12.
Jag frågade klassen hur läraren kunde misstänka att omkrets nio inte var rätt. En elev svarade att omkrets var tvungen att vara ett jämnt tal. För att det är 4 i början (en ruta) och sedan läggs det liksom på 2 när man bygger ut.
Det blev en liten avvikelse i diskussionen och vi pratade om att omkrets förändras som +2, -2 eller +0 när man bygger ut figuren. Och eftersom det börjar med 4, så förblir det alltid jämnt. Detta är ett mycket djupt resonemang som involverar begrepp som invariant och stegvis konstruktion (början till induktion), som traditionellt är tematik för begåvade elever i högstadiet/gymnasiet. Imponerande att vissa elever i åk 5-6 redan har lite känsla för det!
3. Omkretsen för en viss figur är 20.
a) Vilken är den största arean som figuren kan ha?
b) Vilken är den minsta arean som figuren kan ha?
Kom på så många exempel som möjligt på figurer med störst respektive minst area.
Många av elevgrupperna kom fram till att figuren med störst area var kvadraten med arean 25 och med minst area en avlång rektangel (bredd 1) med arean 9. Jag frågade om de hade fler exempel på figurer med area 9 och det hade de, ”teddybjörn med stort huvud” och ”plusplus” tror jag vi kallade dem:
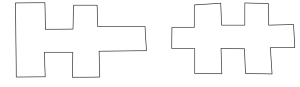
Egentligen funkade många olika lösningar på arean 9 (”böjd pinne” etc.), men med störst area fanns bara kvadraten (som eleverna sade: ”Om det inte får vara en cirkel eller nåt”). Jag sade att man kunde visa det men att det är en för svår uppgift för tillfället.
Förstoring
Precis i slutet pratade vi om vad som hände med arean och omkretsen om en kvadrat får dubbelt så stora sidor. Arean blev 4 gånger så stor! Först tyckte eleverna att omkrets blev 8 gånger så stor (förmodligen för att jag ritade ut de fyra små kvadraterna som den stora består av. Men sedan insåg de att omkretsen blev 2 gånger så stor bara.
Detta gjorde vi för att förstoring och förminskning var vad de individuella uppgifterna handlade om. Dem hann eleverna knappt hålla på med under lektionen, så det blev en (frivillig) läxa.
Tankar efter lektionen
Om möjligt gick lektionen ännu bättre än förra gången. De eleverna som kom för andra gången var de som undervisningen verkligen passade för. Alla gillade aktiviteterna och ingen verkade känna sig så som om denne inte hade där att göra. Mot slutet blev några elever trötta (och började busa lite), så det behövs förmodligen en längre och aktivare rast nästa gång.
Det är roligt att många vågar räcka upp handen och vågar ha fel (även om det är för det mesta samma personer som räcker upp handen om och om igen). Jag har lärt mig 7 av elevnamnen och hoppas att jag ska kunna fånga upp de allra flesta namn vid terminens slut.
Första träffen med Matteklubben, åk 5-6
Matteklubben är Uppsala kommuns satsning på begåvade elever i matematik. Jag har äran att förbereda aktiviteterna som vi håller på med och vara en av lärarna. Här på bloggen tänkte jag lägga ut materialet som vi tar upp på träffarna, samt skriva lite om hur lektionen har gått.
Träffen började med att eleverna tog fika och satte sig ner i ett stort klassrum. Nästan alla de ordinarie platserna blev upptagna (41 stycken). Vi var sju lärare och jag presenterade vad alla hette. Nästan direkt satte vi igång med de blandade uppgifterna. Det enda eleverna behövde var penna och kladdpapper, som de fick låna.
Eleverna fick dela upp sig i grupper om två-tre och i ungefär i 45 minuter försöka lösa fem uppgifter. När de hade löst en uppgift fick de räcka upp handen och berätta lösningen för en av lärarna. Läraren kunde då ställa följdfrågor, som att t.ex. be om att förklara svaret eller fråga om varför det är det enda möjliga svaret.
Under varje uppgift skriver jag några typiska dialoger jag hade med de små grupperna om just den uppgiften.
Blandade uppgifter
1. En pojke har lika många systrar som bröder, men hans syster har hälften så många systrar som bröder. Hur många pojkar och flickor finns det i familjen?
Elev: Hur kan man lösa den här uppgiften när det inte finns några siffror?
Lärare: Försök att pröva dig fram!
Elev: Vi fick att det var 4 pojkar och 3 flickor. Det uppfyller villkoren.
Lärare: Varför kan det inte finnas något annat svar?
2. I tre högar finns 22, 14 respektive 12 nötter. Du får göra tre förflyttningar. Ditt mål är att få högarna att innehålla lika många nötter.
Under en förflyttning får du flytta ett antal nötter från en hög till en annan, men antalet nötter man flyttar måste vara lika med antalet nötter i högen man flyttar till.
Vilka förflyttningar ska du göra?
Elever: Går det här verkligen att göra?
Lärare: Ja :D
Elev: Vi försöker med olika varianter men lyckas inte. (Förklarar hur de tänker.)
Lärare: Vad händer om du tänker baklänges? Vad skulle det sista draget kunna vara?
3. Skriv en siffra till vänster och en siffra till höger om 15 så att det nya talet blir delbart med 15 (det vill säga blir ett tal där divisionen med 15 går jämnt upp).
Elev: 0150, gills det?
Lärare: Försök att hitta på fler svar. (Alternativ: Nej, tal kan inte börja med 0.)
4. På den största ön i Sagolandet finns 4 kungadömen. Varje kungadöme gränsar till de tre andra. Rita karta över ön så som den kan se ut.
Elev: Till exempel så här (visar en cirkel uppdelad i fjärdedelar.)
Lärare: Vi räknar det inte som en gräns om de bara nuddar varandra på hörn, eftersom man inte kan gå över från ett land till ett annat. (Alternativt: Försök att hitta på fler svar.)
5. I en sjö har man placerat en väldig ovanlig vattenlilja. Varje dag så fördubblar liljan sin storlek.
Det visade sig att liljan tog upp precis hela sjön efter 20 dagar. Efter hur många dagar skulle sjön ha blivit full om man hade placerat ut 4 magiska vattenliljor från början?
Elev: Om det tog 20 dagar för 1 lilja, så borde det ta 20/4 = 5 dagar för 4 liljor.
Lärare: Låt oss undersöka om din logik fungerar i andra situationer. Om det hade tagit 4 dagar för en lilja att fylla sjön, så borde fyra liljor göra det på 1 dag, eller hur? (Undersöker lite och kommer fram till att det är 2 dagar i det fallet.)

Det fungerade väldigt bra att kommunicera med eleverna, vi var lagom många lärare (i snitt 5-6 elever per lärare) och ett par grupper hann precis klara av alla 5 uppgifterna när 45 minuter hade gått.
Därefter gick vi igenom varje uppgift på tavlan. En elev fick komma fram och förklara sin lösning och vi försökte alltid att diskutera alternativa lösningar. På uppgift nummer fyra fick alla gå fram och rita sina karta, vi fick väldigt många snygga exempel.
Därefter var det en liten-liten rast och vi skulle komma igång med temat, vilket var kombinatorik. Eleverna fick sitta i grupper om 4-6 och tänka och experimentera med hjälp av färgpennor. Denna gång försökte vi kommunicera med hela gruppen på en gång. Eleverna jobbade i grupp i ca 45 minuter, därefter var det 15 minuter gruppdiskussion.

Innan eleverna satte igång gick vi igenom färgerna som OS-ringarna har och att det har att göra med att alla länder i världen har någon av dessa färger i sin flagga. Därför skulle vi rita olika flaggor med de fem färgerna, men flaggorna behövde inte existera på riktigt.
Flaggor
1. Hur många olika flaggor av följande form kan man skapa om man har tillgång till fem färger?
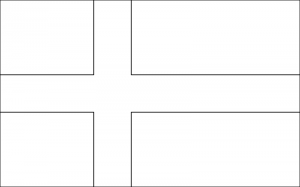
Här förtydliga vi på tavlan att alla de fyra rektanglarna måste ha samma färg. Det dök upp en intressant fråga om korset fick ha samma färg som bakgrunden. Då bestämde vi att man kunde lösa två olika problem, ett där de fick ha samma färg och ett där de inte fick.
Eleverna löste det här på flera olika sätt som genomgången visade (när vi tänker på varianten då de inte fick ha samma färg).
Om korset får vara en av de fem färgerna, så kan bakgrunden ha fyra varianter för färg. Det är likadant för alla fem färgerna på korset. Alltså är svaret 5*4 = 20.
Om man tar två färger, till exempel blå och svart, så kan man göra två flaggor: En med svart kors på blått bakgrund och en med blått kort på svart bakgrund. Det finns 10 olika par av färger (man skriver upp alla möjligheter och kollade att man inte missade något.) Alltså är svaret 10*2 = 20.
Om man får ha samma färg på korset som på bakgrunden, så är svaret 25 (= 5*5). Men man måste räkna bort de enfärgade flaggorna, som det finns precis 5 av, lika många som färger. Alltså är svaret 25 – 5 = 20.
2. Hur många olika flaggor av följande form kan man skapa om man har tillgång till fem färger?

Här dök det också upp frågor om olika varianter: var alla räderna tvungna att vara olika? Fick översta och nedersta vara samma? Fick alla ha samma färg? Vi bestämde oss för att lösa tre olika varianter.
Variant 1: Alla ränderna måste ha olika färger. Några grupper listade ut hur man skulle räkna ut det och tillsammans på tavlan kom vi fram till att svaret blir 5*4*3 = 60.
Variant 2: Översta och understa ränderna får ha samma färg. Någon enstaka grupp listade ut svaret här också. Vi kom fram till att man skulle lägga till något antal till svaret i Variant 1. Man kunde tänka att när understa och översta randen är likadana så är det precis samma situation som med svenska flaggan (mittersta randen är korset, resten är bakgrunden). (Det var en elev som kom på det). Alltså är det 20 varianter vi måste lägga till, så att svaret blir 60 + 20 = 80. En annan elev kom på att vi från början kunde räkna 5*4*4 = 80.
Variant 3: Ränderna får ha vilka färger som helst. Ett par grupper räknade ut att det var 5*5*5 = 125.
Tillsammans på tavlan kom vi fram till att vi behövde lägga till 20 + 20 + 5 till Variant 2 (flaggor där översta och mellersta randen är lika, flaggor där understa och mellersta är lika och flaggor där alla ränder är lika). 80 + 45 = 125 – ett annat sätt att få svaret! Men då tog tiden slut!
3. a) På hur många sätt kan ni i er grupp ställa er på en rad?
b) På hur många sätt kan ni bilda en ring?
Några av eleverna hann testa på den här uppgiften. En del kom fram till rätt svar på a)-uppgiften. Svaren var olika beroende på hur många de var (4,5 eller 6). Men många fick samma svar på b) som på a). Då kom jag med följande invändning:
Lärare: På hur många kan två personer ställa sig på en rad?
Eleverna: Två!
Lärare: På hur många sätt kan två personer ställa sig i en ring?
Eleverna: Ett! Hmmmm…
Lärare: Varför skulle det då vara samma svar för fyra/fem/sex personer?
Uppgiften hann vi tyvärr inte diskutera i helklass, så den tar vi upp nästa gång.
Allt som allt gick lektionen bra för att vara i en så enorm klass. Eleverna blev trötta mot slutet, så nästa gång kommer vi ta en lite längre rast. Det vore också kul om eleverna interagerade mer mellan olika skolor och då kan det vara bra med slumpvis fördelade grupper, som vi kör en mattetävling emellan.
Jag ser fram emot att träffa alla eleverna om fyra veckor! Det är väldigt kul att hålla på med matte med elever som har väldigt god förståelseförmåga. Elever som är inte rädda för att försöka och därför lyckas väldigt bra med att lösa problem som jag är säker på att inte så många vuxna skulle klara.
Pythagoreiska tripplar i form av areor, del 4
I föregående del avslöjade vi processen med vilken vi kan förstora koordinatsystem på så sätt att de förstorade ciklarna innehåller icke-primitiva pythagoreiska tripplar.
Om ett heltal kan representeras som en summa av två kvadrater, så kan vi alltid förstora primitiva pythagoreiska tripplar med detta heltal. Till exempel är 5 = 1+4 = 12+22, alltså en summa av två kvadrattal. Rita då nya rutor (gå 1 steg åt ett håll och 2 åt ett annat) i det gamla koordinatsystemet, rutorna kommer ha area 5. Det betyder att alla areor kommer vara exakt 5 gånger större!
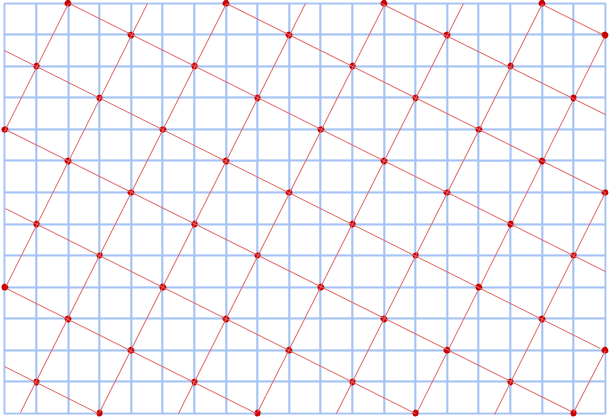
Hur är det med andra förstoringen av primitiva pythagoreiska tripplar, till exempel med faktor 3? Låt oss bevisa att trippeln (9,12,15) inte kan uttryckas i form av rektangelareor på en och samma cirkel. Specifikt undersöker vi hur rektangeln med arean 9 kan se ut.
Givetvis kan det vara en vanlig 3×3 eller 1×9 rektangel, där sidorna går längs med rutnätslinjerna. Men kan en rektangel med arean 9 ligga snett i rutsystemet?
Om en rektangelns ena sida ligger snett, så kommer rutnätspunkterna finnas på den med jämna mellanrum. Låt mellanrummets längd vara a. Vinkelrätt mot första sidan går rektangelns andra sida. Där hamnar rutnätspunkterna med exakt samma mellanrum. Eftersom rektangeln har sina hörn i rutnätspunkter, kommer alltså ena sidan består av k antal a:n och andra sidan av m antal a:n. Det vill säga k och m är heltal, medan a är roten ur summan av två heltalskvadrater.
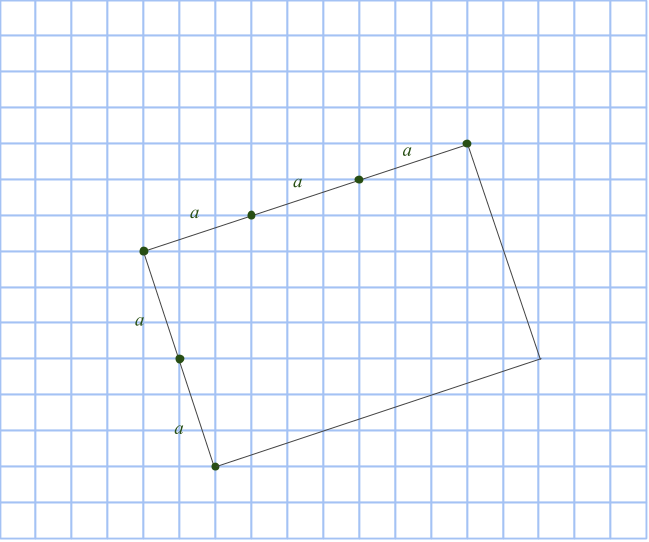
Så arean på en sådan sned rektangel är k*m*a2, alltså en produkt av heltal. Det betyder att om k*m*a2=9, så är a2=1, 3 eller 9. Men varken 1, 3 eller 9 kan skrivas som summa av två positiva heltalskvadrater. Därför finns det inga sneda rektanglar med arean 9.
Överlag måste alltså någon av areans delare kunna uttryckas som en summa av två positiva kvadrattal, för att det ska finnas en sned rektangel med denna area. Det är dessutom ett tillräckligt villkor.
Det betyder att endast två rektanglar har area 9. Rektanglarnas mittpunkt sammanfaller med den omskrivna cirkelns, vi har alltså två varianter.
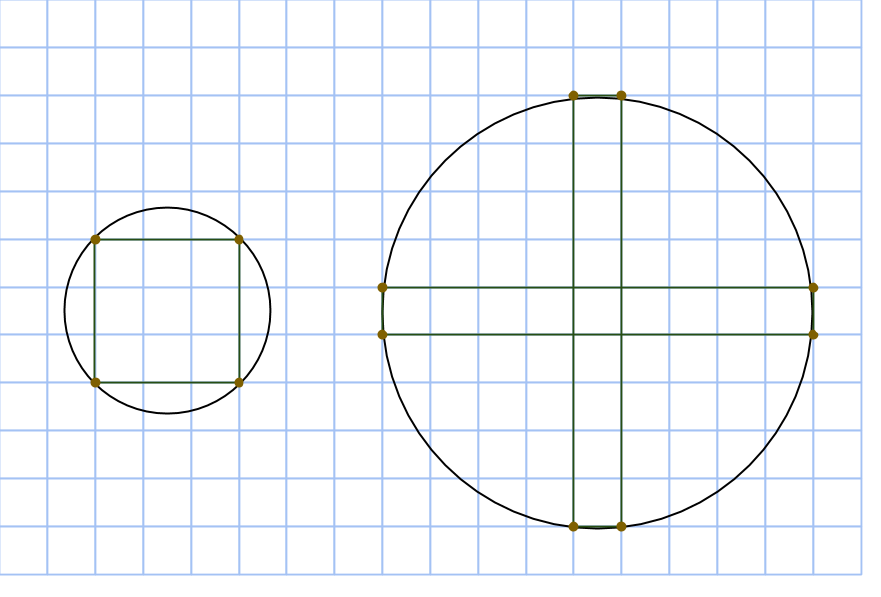
Men den första cirkeln innehåller bara en enda rektangel, medan den andra innehåller den primitiva pythagoreiska trippeln (9, 40, 41) och inga andra rektangelareor. Så trippeln (9,12,15) går inte att konstruera på det här sättet!
Så vi har hittat minst en trippel som inte är konstruerbar på det här sättet. Jag vet fortfarande inte om det är så att alla icke-primitiva tripplar med en faktor, som inte är en summa av två kvadrater, är okonstruerbara. Kanske kan du hitta ett motexempel?
Men denna fortfarande öppna fråga avslutar vi den här serien inlägg om pythagoreiska tripplar i form av areor. Läs gärna serien från början, kanske upptäcker du nya idéer när du läser för andra gången!
Pythagoreiska tripplar i form av areor, del 3
I del 2 såg vi att en primitiv pythagoreisk tripplel alltid kan representeras i form av rektangelareor (inuti rutnätscirklar).
Dyker det upp exakt 3 olika rekatngelareor inuti en sådan cirkel?
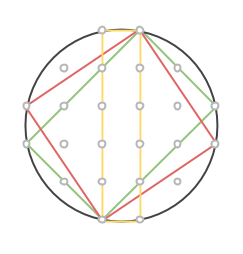
Nej, det kan dyka upp fler än så, vilket beror på att vi kan hitta cirklar där fler än 8 rutnätspunkter hamnar på cirkeln. Nedan ser ni nio olika rektanglar, med areor utskrivna, som vi kan hitta i en cirkel med 16 rutnätspunkter på randen. (Vad tror du förresten är det största antalet rutnätskpunkter man kan hitta på en cirkel?)
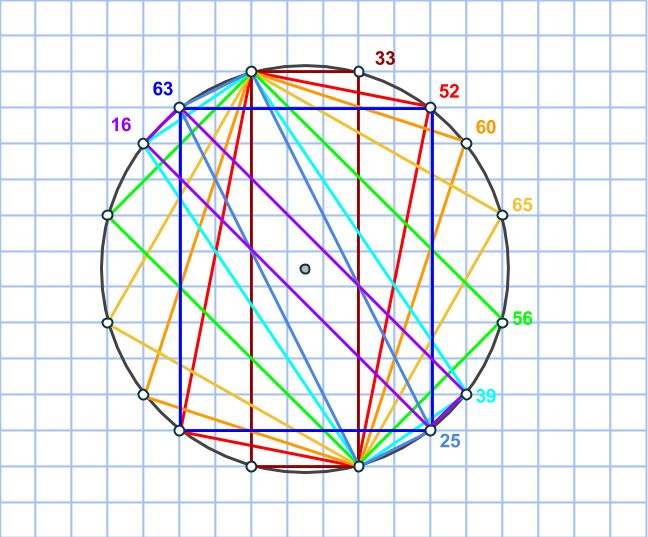
Men hur gör man med icke-primitiva Pythagoreiska tripplar? Konstruktionen från förra delen fungerar inte, eftersom icke-primitiva tripplar kan inte genereras på samma sätt från m och n som primitiva.
En icke-primitiv trippel är däremot lika med en primitiv, multiplicerad med en faktor, som till exempel (6,8,10) är trippeln (3,4,5) multiplicerad med faktorn 2. Om vi på något sätt kunde förstora alla rektanlar med faktorn 2, utan att förlora rutnätsegenskaperna, så skulle problemet vara löst. Men förstorlingen av alla rektanglar med faktorn 2 skulle ske om alla sidor förstorades med faktorn √2.
Detta kan vi göra om vi helt enkelt förstorar hela rutnätet med faktorn √2! Vi gör det genom att rotera koordinataxlarna 45 grader och betrakta fyra punkter som bildar en kvadrat med sidan √2 som en enda ruta. På bilden nedan är det nya rutnätet ritat i rött ovanpå det gamla (eftersom vi trots allt använder det gamla för att rita ut cirklar).
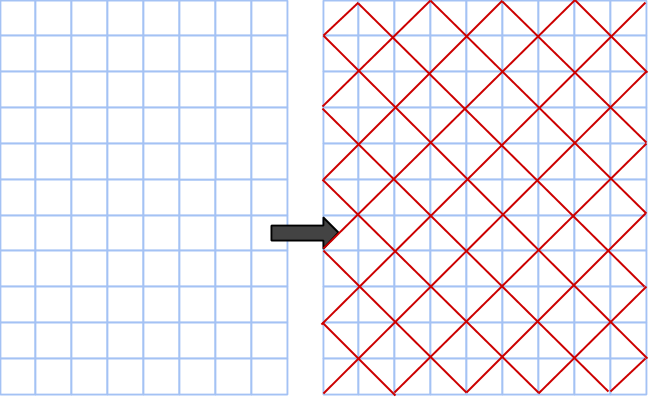
Vi gör samma sak med rutnätscirkeln: rotera och förstora med faktor √2, då bildar från en cirkel med areorna (3,4,5) en annan cirkel med rektangelareorna (6,8,10). Punkterna på cirkeln numreras för det ska gå lättare att se rotationen.
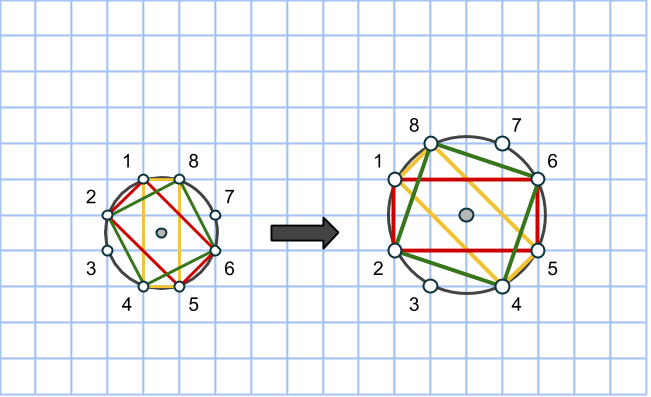
Men såklart kan vi bilda nya rutsystem på andra sätt och med andra rutstorlekar! Bland annat går att att förstora alla areor med 5, med 13 och såklart med produkter av faktorer, som vi redan kan förstora med. (Försök att hitta ett rutsystem med rutlängderna √5). På så vis går det alltså att konstruera alla icke-primitiva taltripplar på formen t.ex. (5*(m2-n2),5*2*m*n,5*(m
Men går att förstora på så sätt med alla faktorer? Går det till exempel att konstruera den icke-primitiva trippeln (9,12,15)? Vi besvarar den här frågan i den sista delen.
Pythagoreiska tripplar i form av areor, del 2
I del 1 såg vi hur vissa pythagoreiska tripplar kunde representeras i form av areor på rektanglar inuti cirklar på rutnät. I den här delen undersöker vi huruvida detta är möjligt för alla primitiva tripplar.
Primitiva pythagoreiska tripplar (a,b,c) är sådana att talen a, b och c inte har några gemensamma delare. Till exempel är (3,4,5) en primitiv pythagoreisk taltrippel, medan (6,8,10) är en icke-primitiv sådan.
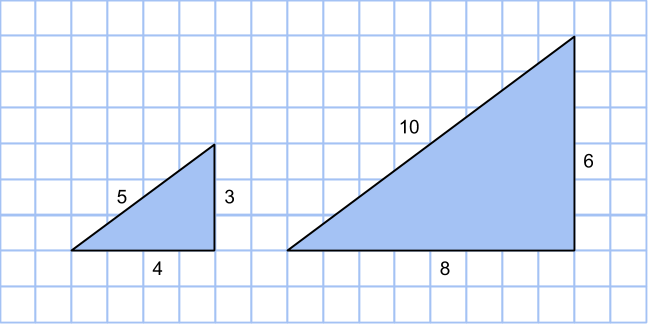
Ur varje icke-primitiv pythagoreisk taltrippel kan vi nämligen få en primitiv: Om de tre talen har största gemensamma delaren d, så kan de skrivas på följande sätt: a = d·r, b = d·s och c = d·t.
Eftersom a2 + b2 = c2, så är även (dr)2 + (ds)2 = (dt)2. Förkortar vi likheten med d2, så får vi r2 + s2 = t2. Således har vi fått en ny pythagoriesk trippel (r,s,t). Den är primitiv, eftersom r, s och t inte kan ha några gemensamma delare (deras gemensamma primfaktorer skulle ha ingått i d).
Ur primitiva taltripplar kan man förstår tvärtom få oändligt många icke-primitiva genom att multiplicera alla tre talen med en och samma faktor.
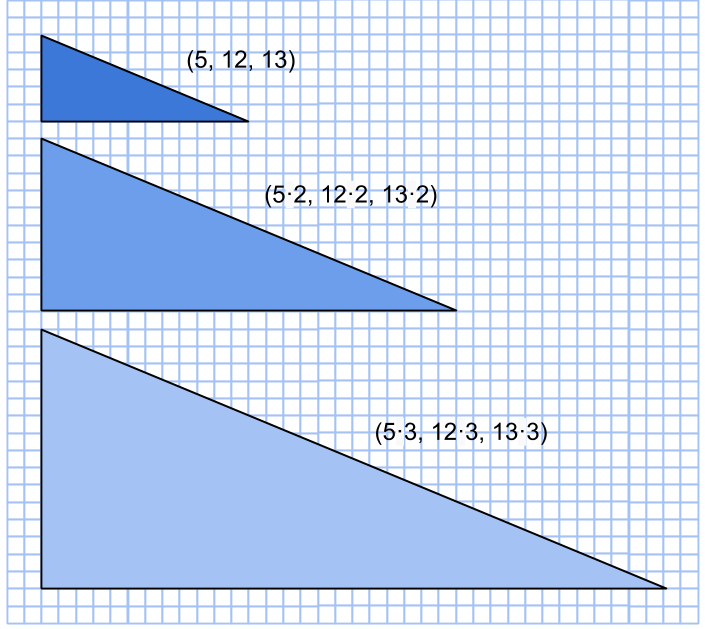
Således finns det oändligt många pythagoreiska taltripplar, men finns det oändligt många primitiva?
Ja, det visar sig att det finns oändligt många sådana och dessutom genereras varje primitiv trippel genom två heltal, som vanligen betecknas m och n. Dessa tal bör vara relativt prima och ett av dem måste vara udda, medan det andra måste vara jämnt. Givet sådana två tal, kommer följande tre tal bilda en pythagoreisk trippel: (m2-n2, 2mn, m2+n2). Kontrollera gärna att oavsett vad m och n är, så kommer Pythagoras likhet gälla för dem.
Till exempel kan trippeln (3,4,5) skrivas som (22-12, 2·2·1, 22+12), det vill säga den genereras av talen 1 och 2.
Talen 3 och 8 ger oss trippeln (2·3·8, 82-32, 82+32), det vill säga (48, 55, 73) och just för det exemplet kommer vi rita upp en cirkel som innehåller rektanglar med respektive areor. Men låt oss beskriva hur vi agerar för allmänna m och n, det vill säga för en godtycklig primitiv pythagoreisk taltrippel.
Talen m och n är nämligen till stor hjälp när cirkeln konstrueras. Vi börjar inte i cirkelns mittpunkt, som man skulle kunna tro, utan på en punkt på randen (en heltalspunkt, som kommer vara hörn för åtminstone en rektangel). Markera en punkt m+n steg nedanför startpunkten, samt m-n steg till höger. Komplettera till en rektangel med en fjärde punkt på rutnätet. Rektangelns area är (m+n)(m-n) = m2 – n2 och dess mittpunkt måste sammanfalla med cirkelns. Vi bestämmer den genom att korsa diagonalerna.
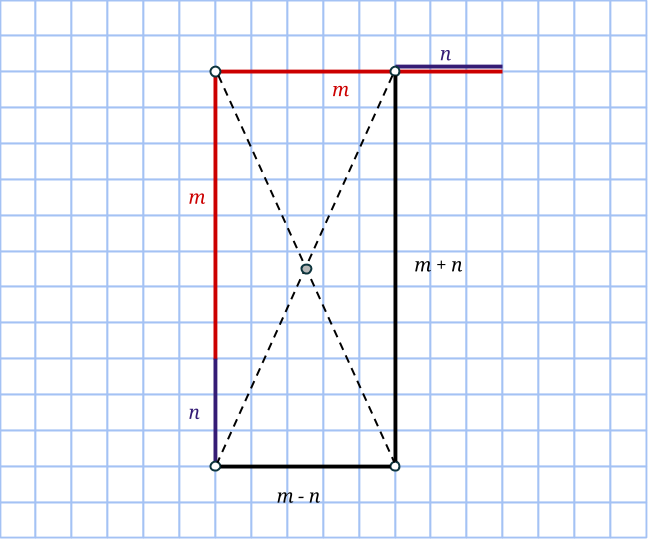
Rektangeln vi har ritat är uppenbarligen inte en kvadrat, så vi får fyra nya rutnätspunkter som också ligger på cirkeln genom att rotera rektangeln 90 grader runt cirkelns mittpunkt:
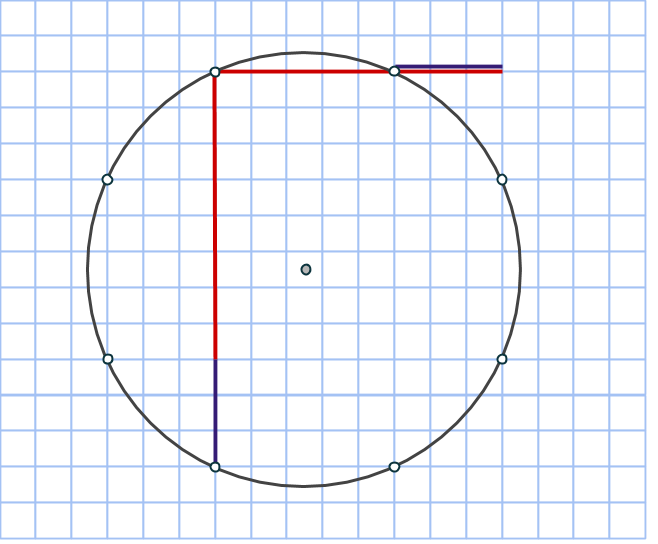
Nu har vi fått en cirkel med åtta rutnätspunkter utsatta och det är faktiskt allt vi behöver! Låt oss bevisa det.
Markera en rektangel som har sina sidor vinklade 45 grader i jämförelse med den första. Kortsidan utgör hypotenusan i en likbent rätvinklig triangel med sida n, medan långsidan är på samma sätt, fast med m. Då kommer alltså arean att vara √(2n2)·√(2m2) = √(4m2n2) = 2mn. Precis som ett av talen i den pythagoreiska trippeln.
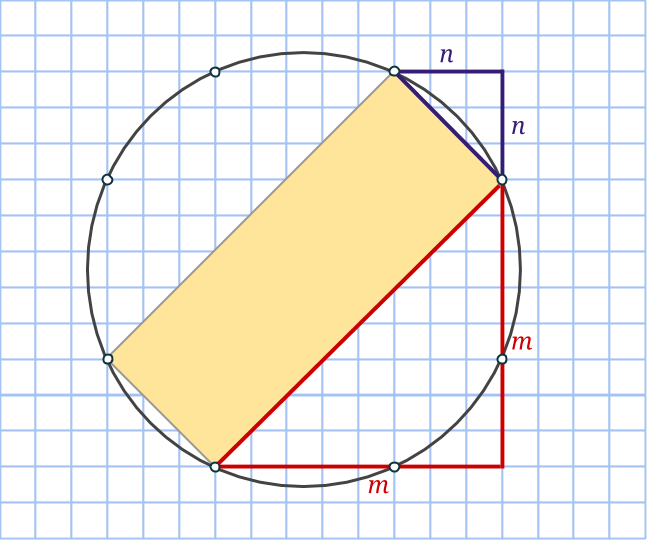
Markera nu en rektangel, som dessutom är en kvadrat genom att ta varannan punkt på cirkeln. Sidan blir lika med √(m2+n2), så arean måste bli lika med just m2+n2. Därmed är den sista arean funnen!
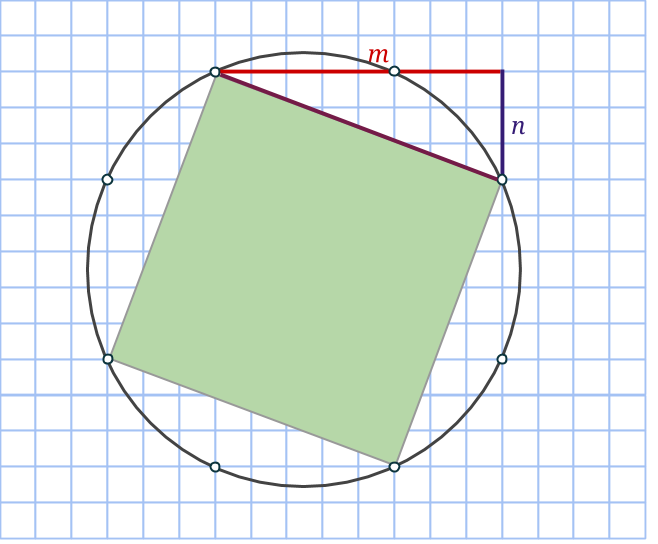
Nu uppstår det fler frågor: Dyker det någonsin upp några extra rektanglar med en annan area vid en sådan konstruktion? Och hur gör man för att konstruera cirklar för icke-primitiva pythagoreiska taltripplar?
Vi försöker besvara dessa frågor i nästa del.
Pythagoreiska tripplar i form av areor, del 1
[kkratings]
Föreställ dig ett rutnät av punkter. Det går att hitta massvis med cirklar som går igenom några av punkterna. En av de minsta sådana cirklarna har hela 8 punkter på sin rand:

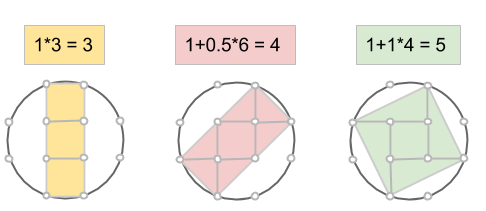
Det går även att hitta några rektanglar inuti sådana cirklar, som har alla sina hörn i punkterna på cirkelns rand (notera att även kvadraten räknas som en rektangel). Kan du bestämma rektanglarnas areor?
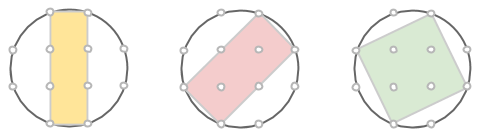
Kan du på samma sätt i cirkeln nedan hitta rektanglar med areorna 5, 12 och 13?
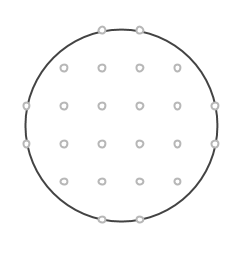
Följande fråga uppstår: går det att hitta vilken Pythagoreisk trippel som helst på samma sätt?
Tärningsspel för små barn
Ett enkel spel med tärningar
Rekommenderas för
Förskolan, lågstadiet, mellanstadiet
Materiel
Ett spelplan (skriv ut nedan), två vanliga sexsidiga tärningar (helst av olika färger), minst 4 pjäser (från ”Fia med knuff” till exempel)
Tid
15 minuter
Antalet deltagare
2+
Regler
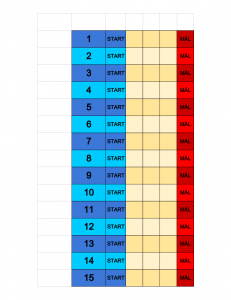
Reglerna är enkla: alla spelarna turas om att sätta ut sin pjäs på något av ”START”-fälten. Bara ett pjäs får stå på varje sådant fält. Det är viktigt vilket fält man ställer sin pjäs på, ställer man bredvid 10 till exempel, så blir 10 pjäsens tal.
Om man är två, tre eller fyra spelare är det bra om alla har minst två pjäser var. Alla kan till exempel sätta ut sin första pjäs, en i taget, och sedan sätta ut den andra pjäsen i omvänd ordning, för att det ska bli så rättvisst som möjligt.
Sedan är dags för själva racet. Man turas om att slå två tärningar, och beroende på vad summan av prickarna blev får en pjäs eventuellt gå fram ett steg (oavsett vem som slog tärningarna). Till exempel, om tärningarna visar summan 3, så är pjäsen som startade vid 3 den som får gå ett steg åt höger. Om ingen pjäs startade vid 3, så får ingen pjäs heller gå fram något.
Den som vinner är spelaren vars pjäs först kommer in i mål, det vill säga den pjäsen som först gick fyra steg fram. Man kan också köra tills tre pjäser kommer in i mål och på så sätt ha en etta, en tvåa och en trea. Bestäm själva beroende på hur ”segt” spelet går.
Naturligvis är det mest intressant att köra flera omgångar!
Vad barn upptäcker själva
Utan att man berättar något annat än reglerna upptäcker barnen några saker själva:
1. Det är dumt att ställa sin pjäs på 13,14,15 och inte heller 1, för den summan kan aldrig visas på två tärningar.
2. 12 och 2 är inte heller så bra tal, för de kommer rätt så sällan.
3. Det är nog bäst att ställa i mitten, på 6-8 nånstans (och det är i princip alltid en av de pjäserna som vinner).
4. Allt det blir så, beror på att det finns många kombinationer det kan bli 7 på (1+6, 2+5, 3+4, 4+3, 5+2, 6+1 ses tydligast om tärningarna har olika färger), men färre på de andra talen.
Som sagt, man säger inte ord, och barn utför matematiskt tänkande själva! Undervisning när den är som bäst :)
Skriv ut ett spel själv
Ladda ner pdf:en med ett färdigt spelplan.
Phi-växter, pi-växter och e-växter, del 2
I del 1 kom vi fram till att en växt inte bör växa med en rationell vinkel. Det vill säga, om vinkeln bladen emellan är 360/(p/q), så kommer växter sabba solljuset för sig själv efter p blad.
Om p=5 och q=2 så växer bladen ut med 360/(5/2)= 144 graders mellanrum. Det innebär att nya blad sprutar ut 144, 288, 432 (det vill säga 72), 216 graders mellanrum i förhållande till det första. Men nästa blad, det sjätte, kommer hamna 360 grader ifrån det första, det vill säga på exakt samma ställe! Detta är väldigt ooptimalt för en växt.
Oavsett vad för rationellt tal vi tar kommer samma elände att hända efter p blad, eftersom då har bladen avlagt 360/(p/q)*p = q*360 grader, alltså ett helt antal varv. Växten vill att det aldrig riktigt ska bli helt.
Så händer det inte med de irrationella talen. Låt oss jämföra vad vi får för irrationella växter. I tabellen ser du en rationell växt, en phi-växt, en pi-växt och en e-växt. Början ser det relativt likt ut emellan alla växterna:
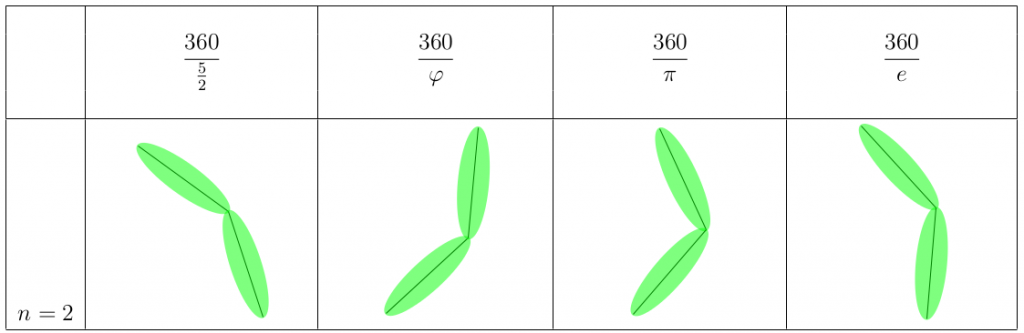
Men efter fem blad har den första växten fördelat sina blad jämnt, medan de andra ser annorlunda ut. Phi-växten har fördelat sina blad ganska bra, medan pi-växten har sina blad onödigt trångt.
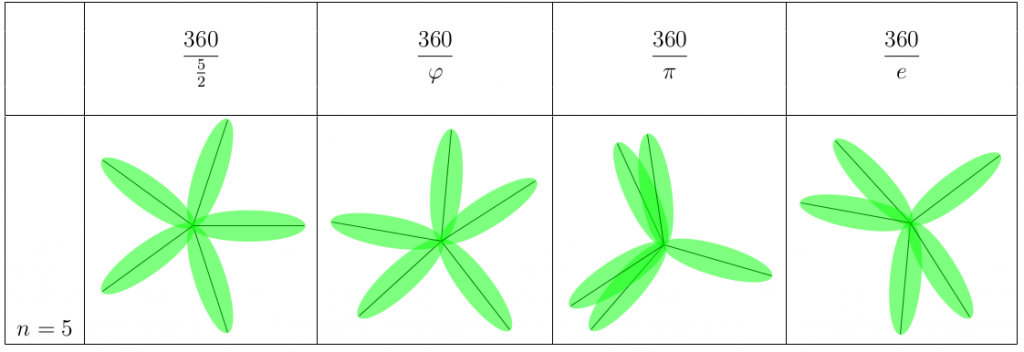
Vad händer vid 12 blad? Oförändrat för den rationella växten – den kan bara ha sina blad på 5 positioner. Phi-växten är jämnfördelad som vanligt, e-växten är också ganska bra. Pi-växten har däremot tre tydliga delar. Kan det ha att göra med att pi på ett ungefär är lika med 3?
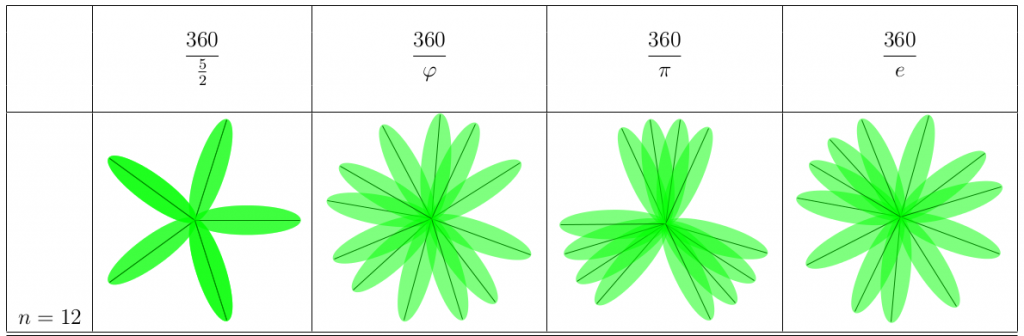
Vi 30 ser vi hur växterna klarar av många blad. De mörkare partierna visar på att bladen överlappar varandra, vilket sker mer och mer på e-växten och pi-växten speciellt. Överlappningen finns hos phi-växten också, men den är mer jämnfördelad. Notera att pi-växten har 22 tydliga delar!
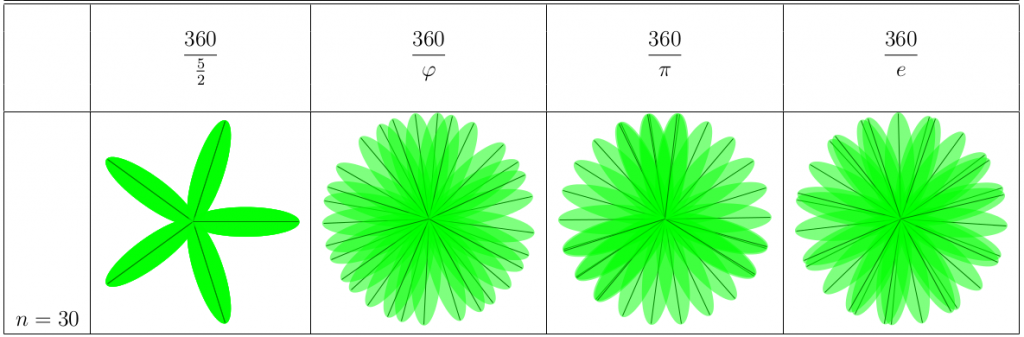
Till sist kollar vi riktigt många blad, 50. Pi-växten har 22 väldigt tydliga delar, e-växten har 19, medan phi-växten aldrig har två blad så pass nära varandra som de andra växterna. Den verkar ha 5 stora delar, vilket tyder på att vi i verkligheten skulle se 5 spiraler för den bladstorleken.
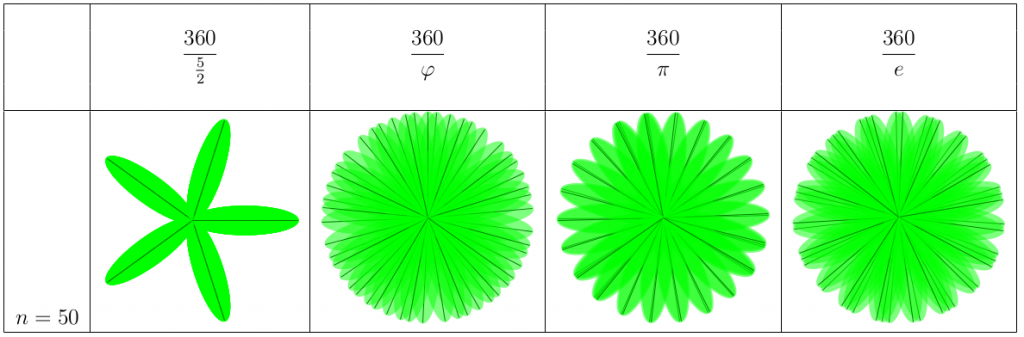
Varför blir det 22 tydliga delar hos pi-växten? Det har att göra med att pi approximeras väldigt bra med talet 22/7 (ca 3,14), vilket får växten att agera som en vanlig rationell växt och överlappa sina egna blad efter 22 stycken. Varför är vissa växter ändå pi-växter, som vi såg i förra delen? Jag gissar på att många verkliga plantor inte har så många blad eller grenar, och därför spelar det inte så stor roll för dem att det blir problem efter 22 stycken. De satsar snarare på 3 eller något sådant.
På samma sätt är 19/7 ett rationellt tal nära talet e (men inte lika när som 22/7 är pi), därför bildas det 19 delar på e-växter. Jag vet inte varför jag inte träffat på e-växter hittills, de verkar ju växa helt ok i början.
Men talet phi är väldigt speciellt. Det finns inte någon rationell approximation av det talet som är i någon mening så bra som 22/7 är för pi. Visst, vi kan använda större nämnare för att få ett rationellt bråk som är så nära phi som vi vill, men då blir nämnarna nästan onaturligt stora. För mer rigorös definition av bra rationella approximationer, se Hurwitz sats. Konstanten i satsen kommer just ifrån phi, det gyllene snittet, och det är det som medför att phi är det mest irrationella talet.
Det innebär att just den konstanten är optimal för växter med stort antal blad, frön, grenar etc. och det är därför vi vanligen finner just 34 och 55 spiraler på solrosor och inte 22 (Klicka på bilden för att räkna själv).