Cthulhu (1 poäng).
”Ni alledels för små för att se detta”, sade Cthulhu till sina 33 barn och skrek ut ”Blunda!”. Alla pojkarna blundade med högerögat, likaså en tredjedel av flickorna. Alla flickorna blundade med vänsterögat, likaså en tredjedel av pojkarna. Hur många barn såg ändå det som de var för små för att se?
Tabellen (3 poäng).
En 4×4-tabell är fylld med talen från 1 till 16. I varje rad, varje kolonn och varje diagonal (inklusive diagonalerna som består av en ruta) är det största talet markerat. Ett och samma tal kan alltså bli markerat flera gånger. Kunde det bli så att
a) alla tal utom två blev markerade?
b) alla tal utom ett blev markerade?
c) alla tal blev markerade?
Stenhögarna (5 poäng).
Det finns tre stenhögar. Sisyfos rullar en sten i taget från en hög till en annan. För varje sten han överför får han ett antal guldmynt från Zeus, som är lika med skillnaden mellan antalet stenar i målhögen och antalet stenar i starthögen (stenen, som rullas mellan högarna, räknas inte in). Om skillnaden är negativ, lämnar Sisyfos tillbaka en respektive summa till Zeus. Om Sisyfos inte kan betala, låter den välvillige Zeus honom att vara skyldig pengarna.
En gång blev det så att alla stenarna hamnade i samma högar, som de fanns i från början. Hur mycket kunde Sisyfos som mest ha tjänat då?
Visa lösningar
Cthulhu (Toomas lösning):
Vi kan notera att en tredjedel av barnen blundade med båda ögonen, det vill säga 33/3=11 stycken. Antalet barn som ändå såg den givna händelsen var då 33-11=22.
Tabellen (Lisas lösning):
Alla tal kan aldrig bli markerade. För att ettan ska kunna bli markerad måste den finnas i ett hörn för att bli störst i diagonalen på en ruta. Det innebär att även tvåan måste befinna sig i en hörnruta. Detta leder i sin tur att även trean måste vara det eftersom den annars aldrig kan befinna sig i en rad, kolumn eller diagonal där den är störst. Samma gäller fyran. Därefter, var man än placerar femman så kommer den aldrig kunna vara störst i sin rad, kolumn/diagonal eftersom det varje ledig rad/kolumn/diagonal finns plats för fler tal.
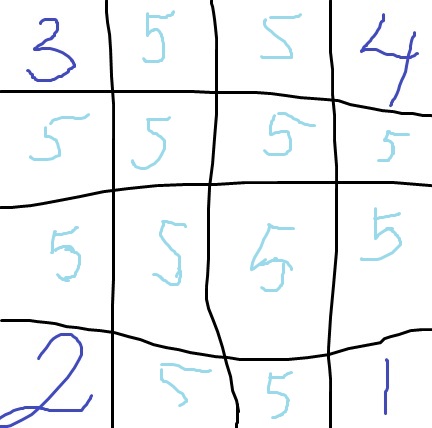
Alla utom ett tal kan bli markerade. Det har jag visat genom genom ifyllning av tabellen nedan. Jag lät femman vara utan markeringar och fyllde i resterande siffror på så sätt att varje nytt tal (större än det före detta ifyllda) fick bli störst i en rad, kolumn eller diagonal.

Alla utom två tal kan också bli markerade. Det har jag visat i tabellen nedan. Jag fyllde i rutorna på samma sätt som ovan, men såg först till att placera sexan i en rad/kolumn/diagonal där den inte skulle kunna vara störst.
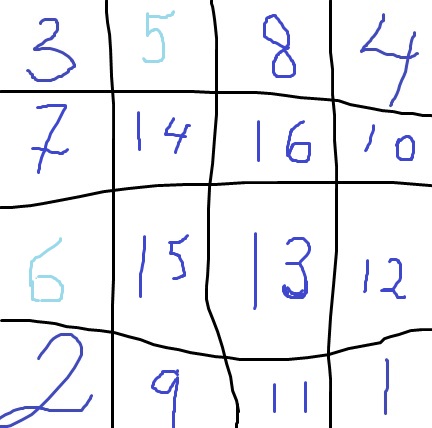
Svar: a) Ja. b) Ja. c) Nej.
Stenhögarna (Davids lösning):
Istället för att säga att han får betalt med skillnaden så säger vi så här: när han flyttar en sten från en hög måste han betala lika många guldmynt som det finns stenar kvar i högen han flyttade från. När han flyttar en sten till en hög får han betalt med lika många guldmynt som det redan fanns stenar i högen han flyttade till. Detta blir samma sak, men ett lite annorlunda sätt att se på saken. Betrakta nu en given hög med stenar och alla överföringar som görs till eller från den högen. Varje gång en sten flyttas därifrån får Sisyfos betala, varje gång en sten flyttas dit får han betalt. Vi vet att det finns lika många stenar i högen i vår slutsituation som det fanns när vi började. Jag vill visa att den totala summan pengar som Sisyfos har tjänat på den givna högen alltid är 0.
Det räcker att visa att påståendet gäller för första gången han återvänder till lika många stenar som det fanns från början. Om det alltid gäller att han tjänat 0 vid första gången han återvänder, så måste det även gälla för alla gånger efter det: han måste ha tjänat 0 mellan första och andra gången, mellan andra och tredje gången o.s.v.
Vidare räcker det enligt samma resonemang att visa att påståendet gäller för första gången han återvänder till något läge som han redan befunnit sig i. Alltså att första gången som det finns två olika tidpunkter då det finns lika många stenar, så har han tjänat 0 mellan dessa två tidpunkter. Om vi kan visa det så kan vi helt bortse från tiden som förflutit mellan dessa två tidpunkter och inse att det måste gälla även nästa gång och nästa och nästa…
Men första gången han återvänder till ett tidigare läge kan endast ske på två sätt:
a) först tar han bort en sten från högen och därefter lägger han till en sten i högen.
b) först lägger han till en sten i högen och därefter tar han bort en sten från högen.
Låt det finnas x stenar i högen. I a) får han då först betala x-1 och därefter får han betalt x-1. I b) får han först betalt x och därefter får han betala x. I båda fallen blir summan 0 vilket skulle visas.
Vi har nu visat att han för varje hög har tjänat exakt 0. Därför är den totala summan som han tjänat för alla högar också exakt 0.



