Mattebloggen

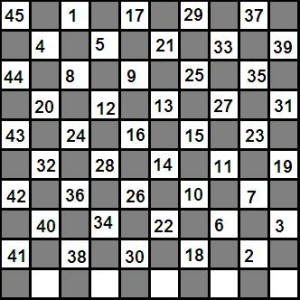
På ett 10×10-bräde finns en pjäs i varje ruta. En tillåten operation är att välja en diagonal som innehåller ett jämnt antal pjäser och ta bort en valfri pjäs från den diagonalen. Hur många pjäser kan man som mest ta bort med hjälp av sådana operationer?

Lösning:

Först och främst uppskattar vi hur många (eller snarare hur få) pjäser måste verkligen vara kvar på brädet.

Från början har vi 18 diagonaler med ett jämnt antal pjäser, och 20 med ett udda antal pjäser, totalt 38 stycken diagonaler. Vi kallar framöver diagonalerna för ”jämna” och ”udda” beroende på vilket antal pjäser som står på dem för tillfället.

Hur förändras detta antal när vi utför operationer? Jo, vi tar ju bort en pjäs från en jämn diagonal, så den diagonalen kommer att bli udda. Men varje pjäs står på två stycken diagonaler. Så den andra diagonalen kommer också att förändra sort.

Så antingen blir det jämn->udda och udda->jämn, vilket totalt sett inte förändrar antalet udda respektive jämna diagonaler eller så blir det jämn->udda och jämn->udda, vilket minskar antalet jämna diagonaler med 2 och ökar antalet udda diagonaler med 2.

På slutet, när vi inte längre kan utföra några tillåtna operationer, kommer antalet udda diagonaler alltså vara minst 20. Men en udda diagonal kan inte vara tom (för att 0 är ett jämnt antal). Så 20 är det minsta antalet icke-tomma diagonaler på slutet.

Varje pjäs kan bidra till max 2 diagonalers ”icke-tomhet”, vilket betyder att det måste finnas åtminstone 10 pjäser kvar på slutet.

Och det finns ett exempel på hur man kan ta bort pjäser på ett sådant sätt att det blir precis 10 kvar. Notera att om brädet målas schackrutigt, så kommer de vita diagonalerna inte ha något att göra med dem svarta (precis som en löpare alltid måste gå på samma färg under ett schackspel).

Därför om vi ta bort pjäserna från de vita rutorna så att det blir 5 kvar, så kan vi göra detsamma med de svarta rutorna (genom symmetrisk borttagning). Så här kan man ta bort från de vita rutorna, siffrorna nedan anger ordningen:

En turist vill ta en promenad i Gamla Stan från busshållplatsen (punkt A) till sitt hotell (punkt B). Han vill ha en så lång rutt som möjligt. Han tycker att det är tråkigt att komma tillbaka till korsningar där han har varit förut, så det undviker han. Rita en så lång rutt som möjligt åt turisten och visa att det inte finns längre.

Lösning:

För att få en så lång rutt som möjligt, måste vi besöka maximalt antal korsningar. Men eftersom varje korsning kundes besökas endasten gång, så går det teoretiskt att göra som mest 35 steg (vi kan gå till alla korsningar utom A).

Men går det verkligen att komma från A till B och på vägen besöka alla rutor? Titta på följande bild:

Här har vi målat korsningarna i ett schackrutigt mönster, varannan svart och varannan vit. Notera att turisten i varje steg byter färg hur han än går.

Men om han börjar i A (vit korsning)och tar 35 steg, så kommer han hamna i en svart korsning (1 steg – hamnar i svart, 2 steg – hamnar i vit, 3 steg – hamnar i svart, 4 steg – hamnar i vit och så vidare).

Men B är inte svart!

Således är det omöjligt att ha en väg som är 35 steg långt.

Däremot går det att hitta på en väg med 34 steg. Det går att göra på många olika sätt, bland annat så:

En turist vill ta en promenad i Gamla Stan från busshållplatsen (punkt A) till sitt hotell (punkt B). Han vill ha en så lång rutt som möjligt. Han tycker att det är tråkigt att komma tillbaka till korsningar där han har varit förut, så det undviker han. Rita en så lång rutt som möjligt åt turisten och visa att det inte finns längre.

En balansvåg har två skålar. Om tyngderna på skålarna är lika visar balansvågen jämvikt. Annars visar den vilken skål som är tyngre. Det finns en stor påse strösocker, en balansvåg samt en vikt på 1g. Hur kan man snabbast väga upp ett hekto strösocker? Observera att om man lägger två sockerhögar i en och samma skål, så blandar sockret ihop sig till en enda hög förstås.

Lösning:

Det finns två saker vi måste göra: dels hitta på ett sätt att få 100 g överhuvudtaget och dels bevisa att det sättet verkligen är det snabbaste. Det är då kanske mer logiskt att göra detta i omvänd ordning: först uppskatta hur många vägningar behövs som minst, och sedan f’örsöka hitta på en algoritm för detta antal vägningar.

I allmänhet, gör alltid först den delen av lösningen som verkar vara enklast. I vårt fall är det ganska lätt att uppskatta en gräns i alla fall. Vi kan mäta hur mycket socker vi maximalt kan väga upp efter ett visst antal vägningar.

Första gången finns det bara en sak att göra: väga upp 1 g socker med hjälp av vikten. (1 g socker uppvägt)

Andra gången kan vi max väga upp 2 g socker till (placera vikten + 1 g socker på ena skålen och uppnå balans genom att hälla socker i den andra skålen). Efter detta har vi engramsvikten, en sockerhög som väger 1 g och en sockerhög som väger 2 g. (3 g socker uppvägt)

Tredje gången kan vi igen ta alltihop på en skål och på så sätt få en sockerhög som väger 4 g. (7 g socker uppvägt)

Fortsätt räkna på samma sätt, det vill säga väg upp så mycket socker som möjligt varje gång. Efter 6 gånger kommer vi ha 63 g socker uppvägt som mest. Det kan vara uppdelat i olika högar, men det är bara 63 g totalt som vi känner till massan för. Alltså räcker det inte med 6 vägningar.

Men går det med 7?

Det går faktiskt, men det är ett lite lurigt sätt. Jag tackar Johan som har berättat lösningen för mig. Djalal hade också en korrekt lösning.

Först observerade vi att man kunde dubbla all vikt man hade. Men genom att strunta i att använda engramsvikten, så kan vi dubblera allt vi hade minus 1 gram. Man kan förstås få dubletter av enskilda småhögar också, eller få en hög som vägde 1 g mer än en annan. Vi kan faktiskt även få en hög som väger 1 mindre än en viss vald, helt enkelt genom att placera den gamla högen på ena vågskålen och engramsvikten på den andra och sedan hälla socker tills det blir balans.

Första vägningen: 1 g vikt = 1 g socker

Andra vägningen: 1 g vikt + 1 g socker = 2 g socker

Tredje vägningen: 3 g socker = 3 g socker

Fjärde vägningen: 6 g socker = 6 g socker

Femte vägningen: 1 g vikt + 12 g socker = 13 g socker

Sjätte vägningen: 25 g socker = 25 g socker

Sjunde vägningen: 50 g socker = 50 g socker

Efter den sista vägningen har vi två högar med 50 g socker i varje, så det är bara att lägga ihop dem. Vi har fått ett hekto strösocker!

En lägenhet består av ett antal rum som kan ha olika areor. Det går att dela lägenheten mellan 2, 3 eller 4 hyresgäster så att varje person får bo på samma area (fast antalet rum kan vara olika). Bestäm det minsta möjliga antalet rum i en sådan lägenhet.

Lösning:

Här gäller det att bestämma det minsta antalet rum så att uppdelningarna är möjliga. Det betyder två saker:

1. Att bestämma något antal rum så att uppdelningarna är möjliga.

2. Visa att för alla mindre antal åtminstone någon uppdelning skulle misslyckas.

Ett sätt att lösa de två punkterna är att gå nerifrån och uppåt, det vill säga starta med så få rum som möjligt (säg 1 rum) och sedan gå vidare till nästa antal, när uppdelningarna inte funkar. Vi testar:

1 rum: går inte att dela upp mellan 4 personer

2 rum: går inte att dela upp mellan 4 personer

3 rum: går inte att dela upp mellan 4 personer

4 rum: om det ska gå att dela upp rummen mellan 4 personer, måste alla ha lika stor area, säg x. Om vi ska dela upp rummen mellan 3 personer, måste en av dem få 2 rum och de andra få 1 rum var. Areorna blir 2x, x, x, det vill säga olika.

5 rum: om det ska gå att dela upp rummen mellan 4 personer, måste en av dem få 2 rum och alla de andra få 1 rum var. Så de senare tre rummen har alla lika stor area, säg x. Då har de första två rummen tillsammans arean x.  Notera att det går då att dela upp lägenheten mellan 2 personer rättvisst. Men går det att dela upp mellan 3 personer? Då skulle de antingen ha föredelningen 2 rum- 2rum-1 rum eller 3 rum-1 rum-1 rum. Notera att sammanlagda arean är 4x, så varje person måste få arean 4x/3. Så de som har enrummare har arean på den lika med 4x/3. Det kan inte finnas två sådana, för att 4x/3+4x/3 är inte lika med x (som ju summan av de två ”icke-x”-rummen måste vara). Så fördelningen måste alltså vara 2 rum-2 rum-1 rum. Då är rumsareorna x, x, x, 4x/3 och 2x/3. Men x, x, x och 2x/3 går inte att fördela jämnt mellan 2 resterande personer. Så det går inte med 5 rum.

6 rum: Försöker vi som förut att bevisa att det inte går, kommer vi fram till att det faktiskt går. Så fort vi har ett exempel, är vi klara. Låt rummen har areorna 1, 1, 1, 3, 3, 3 (m²). Uppdelning mellan 4 personer: 1+1+1, 3, 3, 3, uppdelning mellan 3 personer: 1+3, 1+3, 1+3, uppdelning mellan 2 personer: 1+1+1+3, 3+3.

Jag hoppas att ni fortsätter att klura på förra veckans gåta. Än har ingen hittat lösningen på b). Skicka in frågor och svar på mailet som ni hittar här.

Veckans gåta fortsätter på samma tema som min mattecirkel gjorde i helgen:

En lägenhet består av ett antal rum som kan ha olika areor. Det går att dela lägenheten mellan 2, 3 eller 4 hyresgäster så att varje person får bo på samma area (fast antalet rum kan vara olika). Bestäm det minsta möjliga antalet rum i en sådan lägenhet.

Jag har precis börjat mattecirkeln med Anna, en elev som nu går i nian i Uppsala.

Det är många som frågat mig vad ”mattecirkel” egentligen betyder, för det känns kanske lite dumt att kalla någonting för ”cirkel” när bara två personer träffas. Men jag väljer det namnet av en gammal vana, och för att det är en sorts studiecirkel oavsett hur många som kommer.

Mattecirklar är en gammal tradition i Ryssland och en ganska ny i Sverige. I de flesta fall är det träffar med några stycken elever, som kan ungefär lika mycket matte, och en lärare. Varje sådant tillfälle tar 1-2,5 timmar, lite beroende på elevernas åldrar.

Dessutom för att få lite struktur på det hela brukar lektionerna ha en genomgående tema. Kanske att det handlar om trianglar eller kanske om induktionsprincipen. Målet är att eleven ska förstå en viss idé och prova lite på tekniken genom att lösa problem ur en lista.

Här är lite smakprov vad Anna sysslade med i lördags, temat var ”Uppskatta och ge exempel”. Alla problem kräver förstås förutom svar också motivering. Vill ni ha fler problem från lektionen (de nedan är de lättaste), så är det bara att maila till mig eller skriva i kommentarerna.