Under andra matteträffen med högstadiet hade vi 19 elever som besökte oss. Vi var 3 lärare plus en till som hjälpte lite grann. Det var alldeles lagom för en grupp med elever som inte så ofta räcker upp handen. Men hade eleverna varit lika aktiva som de i åk 2-4, så hade vi lärare inte räckt till. Men som sagt, det var mycket lugnt i klassrummet.
Det är inte så lätt att börja med matematisk problemlösning sent i högstadiet, då man redan har lärt sig en del metoder och hur man brukar göra i matten. Det finns många uppfattningar om hur man bör göra som vi på Matteklubben försöker ändra lite. Det vill säga, vi vill visa dels att man kan göra matte på många olika sätt, dels vill vi lära ut att vara rigorösa i ens tänkande (annars blir det något annat än matte). Det är extra svårt att lära ut något när man ses så sällan!
Det var därför mycket klurigt att välja tema till lektionerna som är lagom svår, men som också är rätt ny för eleverna, där de inte redan har bestämda sätt att göra uppgifterna på. I andra länder är det vanligt att elever stöter på matematisk stringens först när de läser geometri. Samtidigt har vi i Sverige en mattetävling där eleverna presterar sämst just på geometriuppgifterna (mest för att de inte övat på sådana förut). Därför valde jag ”Vinklar” som tema på dagens lektion.
Men jag vill skriva om lektionen som har varit i kronologisk ordning, därför börjar vi med hemuppgiften.
Hemfrågan
Sist i uppgiftsbladet förra gången stod hemuppgiften. Den gick ut på att, med hjälp av att betrakta rester som tiopotenser ger vid division med talet 11, lista ut en delbarhetsprincip för talet 11.
Det var ungefär 3-4 elever som hade tänkt på uppgiften hemma, vilket är glädjande, det betyder att de tyckte att det var tillräckligt intressant och en lagom utmaning. Självklart förväntar jag mig inte att man ska titta på hemuppgiften, då det finns så mycket annat som kallar på ens uppmärksamhet. Men de som tycker att det är kul att utforska ska givetvis göra det, jag försöker att välja lagom uppgifter för det.
Innan vi tog oss an delbarhetsprincipen med 11 och elevernas teorier, repeterade vi beviset för hur man visar att ett tal och dess siffersumma ger samma rest vid division med 9. Mycket för att påminna om hur rester fungerar (att man kan subtrahera tal som är delbara med 9 och få samma rest) men också för att de som var nya på träffen skulle komma in i vad vi höll på med. Jag gjorde en tydligare uppställning än förra gången, då beviset lite hastigt gicks igenom på slutet av lektionen.
Sedan svarade vi på frågorna om vad det blir för rest när man dividerar 100…00 (jämnt antal nollor) med 11 och när man dividerar 100..00 (udda antal nollor) med 11.
I det första fallet tyckte eleverna att svaret var 1, och för att visa det subtraherade vi talet 99..99. Vi diskuterade dels hur många nior det fanns i talet (lika många som nollorna i tiopotensen), dels vad resultatet av divisionen 99..99/11 blir. Eleverna hade inte helt lätt för att svara på den frågan, förmodligen för att de inte är vana vid att jobba med icke-konkreta (stora) tal. Först fick vi svaret 99..9 (en nia mindre), men efter lite rimlighetskontroll förstod de att vi inte hade räknat rätt. En elev formulerade att svaret faktiskt blev 909090..09 (hälften så många nior). Sedan nämnde jag att det ändå inte var så jätteviktigt vad resultatet blev (men att resultatet är ett heltal är en försäkring om att talet verkligen är delbart med 11).
I det andra fallet tyckte vissa elever att svaret fortfarande var 1, men snabbt insåg vi att svaret var 10 (subtraherade talet 999…90 på samma sätt). Hur skulle vi nu kontrollera delbarheten av ett godtyckligt tal med 11?
Likt fallet med delbarhet med 9 gjorde vi ett konkret exempel med ett tal som bestod av några 10000-tal, 1000-tal, 100-tal, tiotal och ental (t.ex. 30000 + 7000 + 400 + 20 + 1). Varannan siffra gav alltså sig själv i rest (3, 4, 1) och varannan gav sig själv gånger tio (70, 20). Vi har förstås en delbarhetsprincip nu (det är bara att räkna ut summan 3 + 70 + 4 + 20 + 1 och se om resultatet är delbart med 11), men den är ju inte särskilt smidigt.
Skulle vi kunna subtrahera något mer, t.ex. från 70? från 20? Vi vill subtrahera något som är delbart med 11 för att inte förändra resten. En elev föreslog talet 66, och vi provade det och fick 4 som svar. Men det är inte självklart hur man från början skulle få den där fyran från siffran sju. På en förfrågning efter andra förslag sade en elev att man kunde subtrahera 77, och då skulle vi få -7 i summan. En annan elev insåg att det var logiskt att ta bort 22 från 20 (och då få -2 i summan). Tillsamman kom vi fram till att resultatet av 3 – 7 + 4 – 2 + 1 skulle ge ett tal med den sökta resten.
Nu bad jag en elev att formulera delbarhetsprincipen med 11, vilket blev att man räknar ut ”varannan siffra plus och varannan minus”. Vi testade slutsatsen på några exempel. På frågan om man skulle börja räkna med minus eller plus nämnde jag att det inte spelade någon roll. Det är inte trivialt varför det spelar någon roll, men jag gav en snabb förklaring om att resultatet blir precis samma, fast med omvänt tecken. Det spelar alltså roll för den exakta resten, men kvittar om vi bara ska bestämma huruvida ett tal är delbart med 11 eller inte.
Det var roligt att tillsammans bevisa den här riktigt svåra delbarhetsprincipen och se att många hängde med. Frågan är om eleverna kan upprepa det på egen hand, när de till exempel förklarar det för någon annan.
Vinklar
Jag valde vinklar som ett avsnitt i geometri, dels för att eleverna redan har mött dem och vet vad det är för något och dels för att många problem i tävlingen HMT handlar om vinklar. Lär man sig tekniken ”vinkeljakt”, det vill säga har vanan att räkna ut vinklar i olika figurer, så kan man komma ganska långt bara på det.
Tyvärr innebar det att eleverna behövde träffa på många nya begrepp på en gång, men jag försökte poängtera att det inte var lika viktigt att lära sig namnet ”alternatvinklar” som att känna till det faktum att sådana vinklar är lika.
Jag ritade upp en bild med två parallella linjer på tavlan, samt en linje som korsar dem. Det bildas många vinklar (åtta), men vilka av dem är lika? Jag tror eleverna redan hade en känsla för det, men det är ju viktigt i geometri att nämna vad som räknas som ett ”vetertaget faktum” (axiom) och vad som inte gör det. Jag pekade på några par vertikalvinklar och sade att de var lika, förklarade vad likbelägna vinklar var (och att det var lika), samt att det då följde att alternatvinklar var lika.
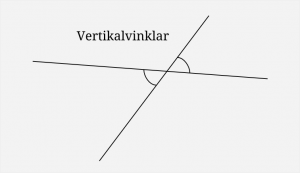
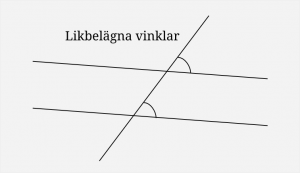
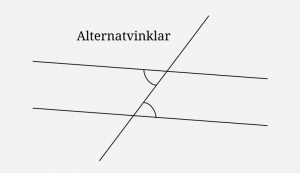
Jag gjorde genomgången av alla tre begreppen på en och samma bild och dessutom lite för hastigt, eftersom jag var ivrig med att komma igång med problemlösningen. Men i efterhand ser jag att det där med ”vedertagna fakta” inte uppfattades av de flesta eleverna. Vi hade tjänat på att gå igenom dessa typer av vinklar noggrannare, långsammare och inte på en och samma bild.
Jag berättade också hur man brukar markera lika vinklar i en figur. Det spelar inte så stor roll vad man väljer för beteckning, så länge alla likadana vinklar är markerade på samma sätt. Man kan markera lika vinklar med lika många bågar eller med lika många streck på bågen eller med ett hjärta om man så vill.
Geometriuppgifter
Eleverna fick lösa uppgifter om vinklar i kanske 35 minuter. De flesta försökte på egen hand, några samarbetade och var två och två. Efter varje uppgift har jag har skrivit upp några av typiska svårigheter och frågor som eleverna (och lärarna) hade, samt hur det gick för dem att lösa uppgiften.
1. Två linjer skär varandra. En av viklarna som bildas är lika med 41°. Vad är de andra tre vinklarna lika med?
Eleverna tolkade som att bilden ”vertikalvinklar” hörde till den uppgiften (eftersom den fanns direkt bredvid). Till elever, som hade svårigheter med frågan, gav jag ledtrådar av typen ”vilka vinklar är lika på bilden?”, ”vad vet man om summan av de alla fyra vinklarna?”. Efter det hade de flesta inga problem med att lösa uppgiften.
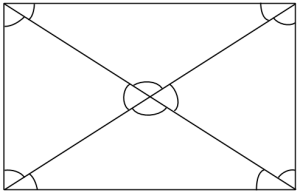
2. Markera så många lika vinklar som möjligt i a) en kvadrat c) ett parallellogram:
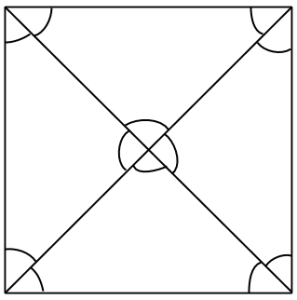
b) en rektangel
c) ett parallellogram
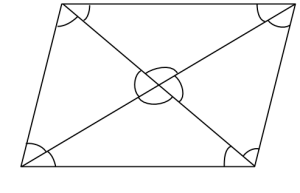
Eleverna hade inga problem med att markera de parvis lika vinklarna (förutom en överanvändning av streck i vissa fall, en vinkel med fem överstrykningar gick inte att skilja från en vinkel med sex överstrykningar, och där gav jag rådet att använda en annan beteckning). Men nästan ingen kunde motivera varför de markerade vinklarna var lika. ”Eftersom de är lika stora”, fick jag höra några gånger. Det var helt nytt med motivering inom geometri för de flesta eleverna. Därför krävde vi inte någon rigorös förklaring på alla egenskaper hos figurerna, men stannade och diskuterade gärna om sätt att dra slutsatser på. Helt enkelt visade vi hur problemen kunde angripas strikt matematiskt.
Till exempel kunde vi fråga varför alla vinklar i mitten av kvadraten (där diagonalerna skär varandra) var lika stora och nöja oss med svaret ”kvadraten består av fyra likadana trianglar”. Men ingen refererade till ”likbelägna” eller ”alternatvinklar”, antagligen på grund av ovanan vid axiomatiskt resonerande (eller min hafsiga genomgång). Skönt i alla fall att eleverna höll med Euklides om att dessa axiom gäller :)
3. Vad är vinkelsumman i a) en triangel? b) en fyrhörning?
Här skrev de flesta eleverna ner rätt svar, men nästan ingen hade någon som helst motivering till det. På grund av detta stannade vi upp i den enskilda problemlösningen och hade en gemensam slutledning om varför vinkelsumman i en triangel alltid är 180° (ALLA visste det, men INGEN hade sett något bevis för det). Eleverna hittade på ett spännande sätt som gick ut på att kopiera triangeln och lägga den upp och ner ett par gånger. Vi behövde fortfarande använda ”alternatvinklar”-axiomet, men det sjönk nog ändå inte in att vi använde det. Det kommer ta ett tag innan gruppen är vana vid bevis!
Vad gäller förhyrningen så hade ett par elever bra idéer som gick ut på att en fyrhörning består av två trianglar (vilket ju egentligen räcker för att bygga ihop ett riktigt bevis). Vi gick igenom det på slutet av geometrimomentet och då tog jag även upp icke-konvexa fyrhörningar.
4. En linje skär två andra parallella linjer. Bestäm vinkeln mellan de mostående inre vinklarnas bisektriser.
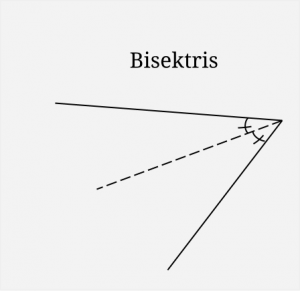
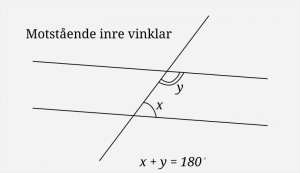
Eleverna som satte sig in i uppgiften kunde hitta lösningen genom att kombinera dessa två definitionsbilder. Jag kan tänka mig att om uppgiften skulle ha tagits upp på någon annan träff, så skulle en del inte kunnat lösa den. Men i samband med temat ”vinklar” och ett par ledande bilder blir den tvärtom ganska lätt.
5. Går det att rita fem strålar från en punkt så att det bildas exakt fyra spetsiga vinklar mellan strålarna? Vinklar mellan varje par av strålar räknas, inte bara mellan grannstrålarna.
Det behövdes några förtydliganden för vad som gäller i den här uppgiften, men de flesta hade en intuitiv känsla för vad strålar och spetsiga vinklar är för något. Under genomgången fick en elev komma fram och visa sitt exempel (som för övrigt inte är trivialt att konstruera). Totalt var det kanske 5 elever som hade löst uppgiften (och velat gå fram till tavlan).
6. Yttervinklarna för triangel ABC vid hörnen A och C är lika med 115° respektive 140°. En linje, som är parallell med AC, skär sidorna AB och AC i punkterna M och N. Bestäm vinklarna hos triangeln BMN.
En fråga som många av eleverna (och till med någon av lärarna!) inte visste svaret på, var vad ”yttervinkel” är för något. En av lärarna läser inte uppgifterna i förväg av pedagogiska skäl, det vill säga för att titta på uppgifterna med samma nya ögon som eleverna på lektionen. Men kanske är det inte en strategi som håller. Det var hur som helst det ordet eleverna fastnade på. Men ett par elever hann ändå klara uppgiften, med det var inte jag personligen som lyssnade igenom lösningarna.
Allt som allt var geometri och vinkeljakt ett svårt ämne, framförallt för att eleverna var så ovana. Fördelen är att alla då är på samma villkor, ingen hade mycket mer förkunskaper än någon annan. Jag hoppas att eleverna gillade att upptäcka nya saker om vinklar och bevisföring. Om någon inte gjorde det, så kan det bero att det var ett för stort kognitivt steg att direkt hoppa in i bevisens värld eller så gillade kanske inte personen att hålla på med helt nya saker (och kanske hellre ville syssla med något bekant). I det senare fallet tror jag inte Matteklubben är en rätt aktivitet för personen, då vi kommer att hålla på med nya tankesätt varje träff.
Bevis
Som jag har nämnt ovan, att motivera sina lösningar från grunden (använda sig av axiom) var någonting som var helt nytt för eleverna. När man pluggar matte möter man ofta olika typer av bevis (till exempel beviset för Pythagoras sats), men man ombes inte alltid att konstruera bevis själv. Egentligen är en motiverad lösning till vilken uppgift som helst ett bevis i sig, men brukar inte kallas för det. Därför är många universitetsstudenterna rädda för att hitta på bevis, de förstår inte hur man går till väga.
Tanken är att eleverna på Matteklubben så småningom inte ska bli rädda för att motivera saker så utförligt som möjligt. Det handlar dels att lära sig om vad som är allmänt vedertaget fakta (t.ex. behöver man inte bevisa att 1 + 1 = 2, trots att det egentligen går att motivera), med också vad som inte är det. Och dels om att bli säker på att man inte missat några möjligheter i sitt bevis. Den känslan utvecklas när man blir bra på logik och kombinatorik, vilket vi ofta övar på när vi löser blandade uppgifter.
Jag har bloggat om bevis tidigare: Vad är ett fullständigt bevis?, Att bevisa. Ett exempel på ett bevis hittar du här: Klassiska bevis: roten ur 2 irrationellt.
HMT
I samband med att tävlingen HMT hålls den 11:e november ville jag lägga ner en del av lektionen på att informera om den och att träna inför den genom att lösa gamla problem. Bara några stycken i gruppen hade hört talas om Högstadiets Matematiktävling, vilket kanske inte är så konstigt, eftersom få skolor i Uppsala har deltagit de senaste åren. (En elev som var med på första träffen hade dock gått till final förra året och presterat bra!)
Eleverna som går i Matteklubben är de mest lämpade att delta, men för att de ska kunna göra det, behöver deras lärare vara delaktiga. Därför fick alla ett informationsblad som de kunde ge till sina respektive lärare. Sista anmälningen är den 4:e november och det går att läsa mer om tävlingen på HMT:s hemsida.
Jag hoppas att några elever vill delta, de har en god chans att ta sig vidare till final! Oftast behöver man lösa ungefär 4 problem (av 6) för att gå vidare. Men det är förstås frivilligt och man ska bara tävla om man tycker att det är kul.
Övning inför tävlingen
Vi hade bara någon halvtimme kvar av lektionen för att öva på gamla HMT-problem. Men klassen hann lösa alla uppgifter en minut innan lektionen skulle sluta! Det vill säga varje uppgift löstes av åtminstone en elev. Även om jag sade att uppgifterna inte var ordnade i svårighetsgrad, så försökte de flesta ändå att lösa uppgifterna i ordningen de stod, det är ju svårt att avgöra svårighetsgraden innan man har ett hum om uppgiften.
Utvärdering
Som det märks från mängden material som vi hinner ta upp under en lektion, så kan eleverna ta in en hel del kunskap. Men de har inte riktigt lärt sig att tillämpa allt vi pratar om. Det är inte så konstigt. Det är ganska lätt att visa häftiga saker för intresserade elever, kanske berätta om sitt eget sätt att se på matte eller visa en naturvetenskaplig grej som någon annan har kommit på (sådant som förekommer på tekniska museer). Men det är svårt att lära ut genomförande, det vill säga förmågan att komma på egna häftiga saker. Det tar många år av arbete och träning.
Det är dock väldigt viktigt att ta vara på intresserade elever, eftersom de i framtiden kommer att kunna bli riktigt bra ingenjörer eller forskare (eller något annat häftigt). Målet är ju att de ska komma på nya saker och därför behöver de att träna på den förmågan. Däri ligger Matteklubbens styrka och utmaning! Det finns hur mycket som helst i matematiken som bjuder in till upptäckter, men det gäller att välja sådan material som passar eleverna. De ska ha en chans att både göra upptäckter som någon annan har gjort före dem, men också ha möjligheter för att hitta på helt nya lösningar!
