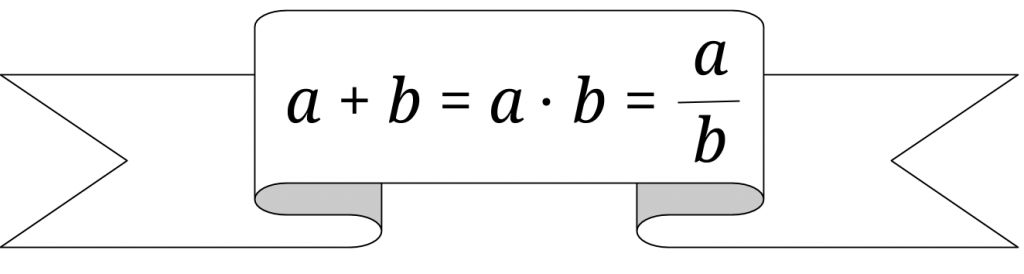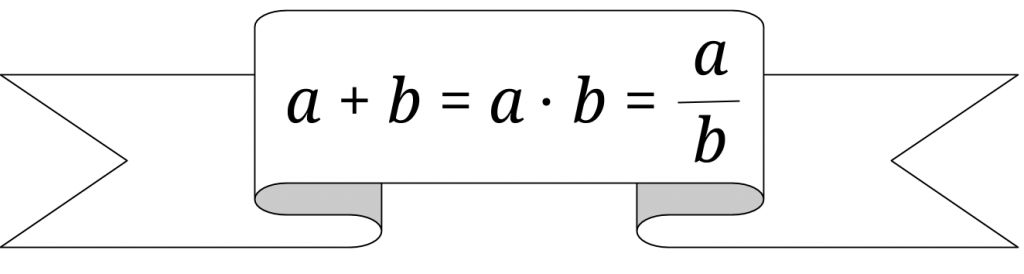Välkommen till Mattebloggen! Här nedan kan du få reda på lösningen på kluringen.
Finns det två tal, sådana att deras summa, produkt, samt kvot sammanfaller?
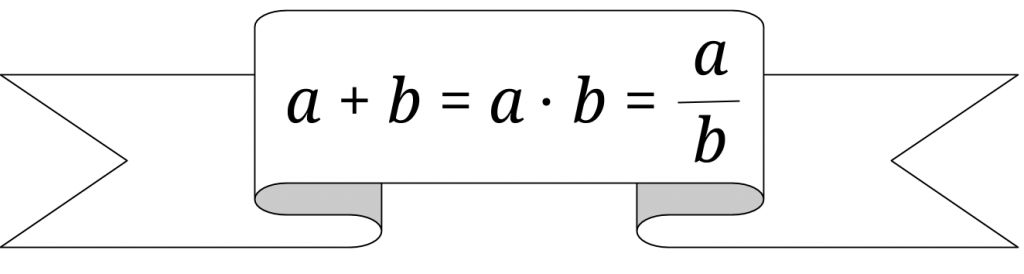
Visa lösningen
Antag att sådana två magiska tal a och b existerar.
Om a * b = a/b, så måste a * b * b = a. Det betyder att a = 0 eller b * b = 1.
Men a kan inte vara lika med 0, för då vore 0 + b = 0 * b = 0, det vill säga b = 0 också. Men kvoten 0/0 är inte lika med 0.
Därför är b * b = 1, således b = 1 eller b = -1.
Men om b vore lika med 1, så skulle a + 1 = a * 1 = a, vilken inte kan vara sant.
Så b = -1 och vi har att a – 1 = a * (-1) = a/(-1).
Om a – 1 = -a, så gäller 2a = 1, det vill säga a = 1/2.
a = 1/2, b = -1 är en fungerande lösning, och det är även den enda lösningen.