Myntpåsar
Lydia har två påsar och 100 mynt. Hon måste fördela alla mynten i påsarna så att en påse innehåller dubbelt så många mynt som den andra. Mynten får inte delas itu. Hur ska hon göra?
Roligare matematik
Lydia har två påsar och 100 mynt. Hon måste fördela alla mynten i påsarna så att en påse innehåller dubbelt så många mynt som den andra. Mynten får inte delas itu. Hur ska hon göra?
© 2009-2024 Mattebloggen
Jaha, då har vi löst den här också. Kom med nåt svårare nästa gång!
DUNK!
På vilket sätt löste ni den?
Jaha jag löste den redan klockan 9:40. Dunk!
Jag löste den dock 9:39! Dunk!
Tyvärr så hann jag före jag löste den redan klockan 07:10. Dunk, dunk!
Nä nu får ni va tysta. Vi löste den 6:40 men vårt inlägg publicerades 9:41. Supermegaultradunk!!!
Är då någon av er villig att presentera en lösning? Det skulle vara väldigt intressant att höra andras tankar om detta problem.
Du kan ju lägga ena påsen i den andra, sen får du lösa den själv!! ;D
Intressant. Jag tänkte aldrig på att den ena mängden även kunde ha en annan mängd som ett av sina element.
Detta bör kunna generaliseras. Eventuella frågeställningar är:
– Vad händer om antalet mynt är udda istället för jämnt?
– Vad händer om vi ökar antalet påsar?
Ja ett likartat problem skulle kunna vara att du har femtio mynt och ska fördela dem på fyra påsar så att varje påse innehåller dubbelt så många mynt som den andra. Du erhåller ekvationen x + 2x + 4x + 8x = 50 ,vilken naturligtvis är olösbar då du inte får dela mynten i mindre bitar.
Ovanstående problem skrevs av hamstergrillaren.
Fast även här kan vi utnyttja faktumet att en mängd kan vara ett element i en annan mängd, det vill säga att vi kan lägga en påse i en annan. Detta förbiser du i din ekvation.
Om vi tillämpar detta faktum på det föreslagna problemet kan vi utgå från att den största påsen innehåller 50 mynt. Den näst största innehåller då 25 mynt, men därifrån kommer vi inte vidare. Detta beror på att vid varje iteration så delas talet i två. Antalet möjliga iterationer blir då antalet gånger ursprungstalet kan delas med två, eller med andra ord, hur många tvåor det finns i primtalsfaktoriseringen av talet.
Generellt kan vi säga att för att lägga K mynt i N påsar på ett sådant sätt att antalet mynt i varje påse fördubblas för varje led från den minsta till den största, så krävs det att K kan skrivas på formen K=(2^(N-1))*M, där K, N och M tillhör de naturliga talen. Skälet till att exponenten är ett mindre än antalet påsar, är att antalet iterationer är just det. Skälet till att M är en faktor till K är att alla naturliga tal inte kan skrivas på formen K=2^(N-1), med andra ord att alla naturliga tal inte är tvåpotenser.
Om vi vill generalisera ytterligare så har vi att för att lägga K mynt i N påsar på ett sådant sätt att antalet mynt i varje påse ökar med an faktor av L från den minsta till den största så krävs det att K kan skrivas på formen K=(L^(N-1))*M.
Vi kan utnyttja den första formeln på det givna problemet. Vi har redan konstaterat att K=50 leder till att en sådan uppdelning inte kan göras. Detta kan vi även visa med hjälp av formeln. Vi har att 50=(2^4-1)*M, vilket kan förenklas till 50=8M. I detta fall tillhör M inte de naturliga talen, vilket var ett kriterium. Alltså går uppdelningen inte att göra.
Vilket är då det minsta K där den givna uppdelningen kan göras? Vi har att K=(2^(4-1))*M ⇔ K=8M. Det minsta nollskilda K som är ett naturligt tal fås av att M=1, vilket leder till att K=8.
För övrigt, är termen iteration korrekt använd i denna text? Jag är olyckligtvis inte särskilt bekant med den.
Jodå, iteration tror jag är lämpligt att använda. Kul att ni kommer på egna problem här inne!
Och lugna er, 7NM, det kommer en svårare gåta på måndag!
Toomas: Vad jag ville visa med ekvationen var just det du sade nämligen att även i detta problem måste vi utnyttja samma faktum som i ursprungs problemet med Lydia. Svaret är således följande: Lägg fem mynt i en påse som du lägger i en annan påse som redan innehåller fem mynt. Därefter har du två påsar och 40 mynt kvar lägg sedan tjugo mynt i en tredje påse som läggs i en fjärde påse som även den innehåller tjugo mynt. Nu är alla påsar och alla mynt uppdelat enligt följande mönster:
Påse 1: 5 mynt
Påse 2: 10 mynt
Påse 3: 20 mynt
Påse 4: 40 mynt
Varje påse innehåller alltså dubbelt så många mynt som föregående och vi har därmed lösningen på problemet!
Intressant iakttagelse, Hamstergrillaren. Den visar att formeln som jag formulerade behöver revideras.
Det du har utnyttjat är att antalet mynt, K, kan skrivas som en summa av ett flertal termer på ett sådant sätt att K=K_1+K_2+…+K_n. I det beskrivna fallet har vi K=K_1+K_2=10+40.
Uppdelningen går då att göra om och endast om K kan skrivas på formen
K=K_1+K_2+…+K_n=((L^(N_1-1))*M_1)+((L^(N_2-1))*M_2)+…+((L^(N_n-1))*M_n). Den tidigare formeln var endast ett specialfall av denna.
Vi har här att K=K_1+K_2=10+40=((2^(N_1-1))*M_1)+((2^(N_2-1))*M_2) som har lösningar i de naturliga talen. Vi har i och med detta visat att en uppdelning är möjlig att göra i detta fall.
Stämmer detta, eller behöver formeln revideras ytterligare?
För övrigt, är det möjligt att skriva med hjälp av LaTex här?
Jag testar lite att skriva med LaTeX: och
och 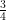 .
.
Japp, det verkar gå. Sätt två dollartecken på var sin sida om formeln helt enkelt.