[kkratings]
Föreställ dig ett rutnät av punkter. Det går att hitta massvis med cirklar som går igenom några av punkterna. En av de minsta sådana cirklarna har hela 8 punkter på sin rand:

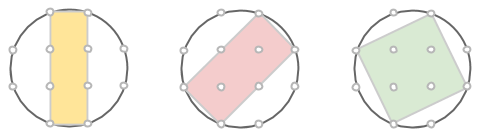
Det går även att hitta några rektanglar inuti sådana cirklar, som har alla sina hörn i punkterna på cirkelns rand (notera att även kvadraten räknas som en rektangel). Kan du bestämma rektanglarnas areor?
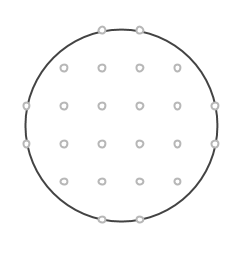
Kan du på samma sätt i cirkeln nedan hitta rektanglar med areorna 5, 12 och 13?
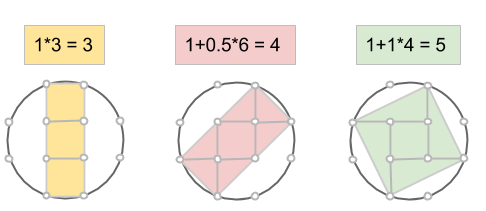
Följande fråga uppstår: går det att hitta vilken Pythagoreisk trippel som helst på samma sätt?

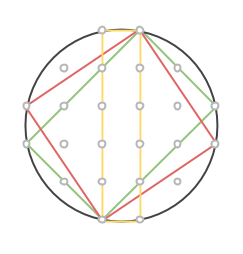
I alla (två) exemplen så är de enda möjliga rektanglarna de som korresponderar mot pythagoreiska tripplar (och kanske rektanglar med area noll om man känner sig singulär). Är det något allmänt eller är det bara för att det är så små cirklar? Jag har för mig att 9,40,41 cirkeln beter sig likadant.
Johan, det har att göra med att det är små cirklar och att det i allmänhet inte så ofta tal beskrivs som en summa av två kvadrater på två olika sätt. När det händer smälter två cirklar ihop och det bildas många extra rektanglar. Så inget som gäller allmänt och jag kommer visa ett exempel i del 3.