Öriken
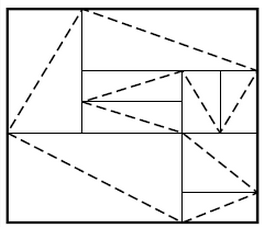
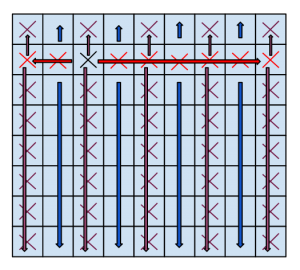
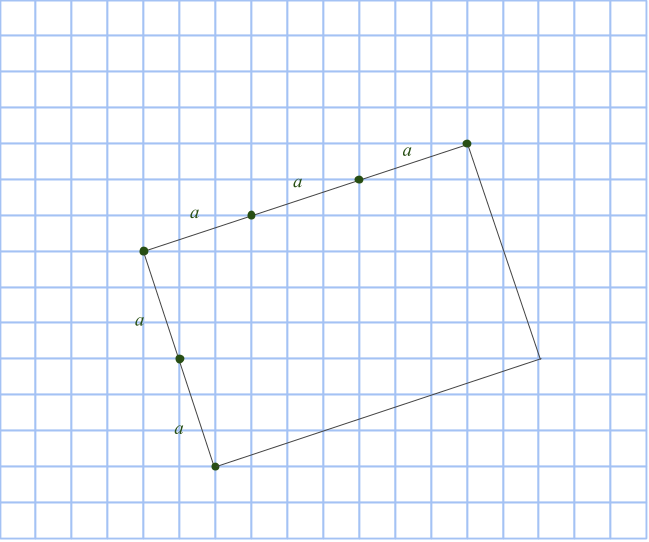
Det Stora och det Lilla Riket är båda rektangulära öar och uppdelade i rektangulära landskap. I varje landskap finns en väg som går längs med en av diagonalerna. På varje ö bildar vägarna en sluten rutt, som inte går igenom någon punkt flera gånger. På bilden ser du det Lilla Riket, som har 6 landskap:
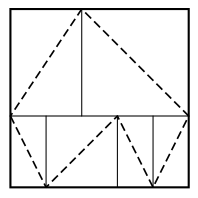
Det Stora Riket har däremot ett udda antal landskap. Hur många landskap kan det Stora Riket som minst ha?
Att räkna utan tal och bokstäver
När någon ställer frågan ”Vad är matematik för dig?” svarar jag ibland ”Att tänka.” Det kan tolkas som ett luddigt svar eller att jag kanske tror att matematik är viktigare än allt annat. Men så är inte riktigt fallet och jag ska försöka visa vad jag menar med hjälp av ett exempel.
Problem
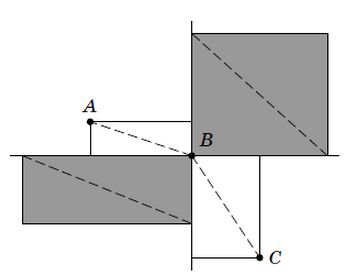
Framför dig är en rektangel. Du sätter ut två punkter inuti rektangeln och förbinder alla de med alla hörnen, till exempel så som bilden visar. Vilken area är störst: den svarta eller den grå?
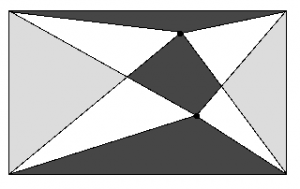
Försök att tänka ut svaret utan att använda dig av några som helst variabler eller uträkningar. Svårt, eller hur?
Låt mig presentera ett tankesätt som gör den här uppgiften väldigt lätt istället.
Fläckar
Föreställ dig ett vitt A4-papper och ett litet barn som målar med blått och gult akvarellfärg. Hon målar abstrakt konst, det vill säga det gula blir någon slags oregelbunden fläck, det blå likaså. Barnet målar inte så noggrant, på vissa ställen täcker fläckarna över varandra och på så sätt bildas det gröna områden.

När bilden blev färdig visade det sig att den sammanlagda arean av de två fläckarna är lika stor som arean av hela pappret. Visa att den gröna arean är lika stor som den vita arean.
Beviset får vi genom att ställa den enkla frågan: ”Hur mycket area behövs för att komplettera den blå, den gula arean och den gröna arean till arean av hela pappret?” Visuellt behövs bara den vita arean, för att det är den som är kvar. Men om vi tänker på att fläckarna tillsammans skulle utgöra arean av hela pappret så ser vi att det saknas en till grön area för det. Det gula och det gröna är nämligen en hel fläck, men det blåa saknar just det gröna för att bli en hel fläck (eller tvärtom). Eftersom det saknas precis lika mycket när vi tänker på två olika sätt så måste den gröna arean och den vita arean vara lika stora.
Vi löste uppgiften utan att använda oss av X eller någon annan variabel. Egentligen resonerade vi precis som men gör med ekvationer, men med ord istället. Ibland kan det vara lättare, ibland svårare, men här är det mer intuitivt tycker jag, speciellt om man ska förklara lösningen för någon annan!
Tänka geometri
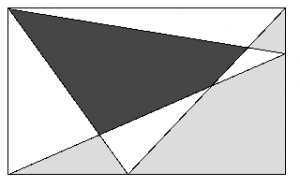
Vad har uppgiften med abstrakta fläckar med riktig geometri att göra? Låt oss bevisa att den svarta och den grå arean är lika i följande figur:
Vi kan även tänka att regelbundna former utgör fläckar. I följande figur kan vi göra om färgerna till gult, blått, grönt och vitt. Ser du de två fläckarna? Och att det gröna är precis skärningen de emellan och det vita är precis den delen de inte täcker?
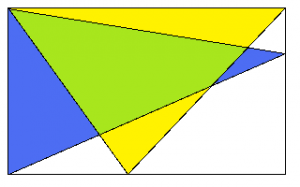
För att visa att den gröna arean är lika stor som den vita behöver vi bara förklara varför trianglarna tillsammans utgör arean av hela rektangeln. Varje sådan triangelarea utgör hälften av rektangelns area (för detta kan vi t.ex. använda areaformlerna, för rektangeln är det basen gånger höjden, men för triangeln är det precis hälften av det). Alltså utgör summan av areorna på trianglar exakt hela rektangelns area. Klart!
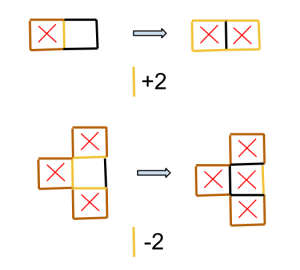
Kan du identifiera fläckarna i den ursprungliga uppgiften och lösa den utan att räkna alls? Kom ihåg att fläckarna kan ha godtycklig form och behöver inte ens vara sammanhängande!
Uppgifter utan räkning
Detta är vad jag menar med att ”tänka matte” istället för att ”räkna matte”, vilket är det uttrycket de flesta använder (eftersom de oftast gör just det senare, men inte det första).
Siffror och variabler är bra att införa när de behövs, men det finns fördelar med att försöka klara sig utan dem. Det kan vara tillräckligt för att lösa ganska komplicerade problem, som till exempel uppgiften i början. När vi presenterar idéer, uppgifter och lösningar av den typen för barn blir de oftast inte rädda, då det bara finns ord och bilder. Barn har inte fördomar mot resonemang med ord, till skillnad mot variabelräkning. Där har fördomarna oftast utvecklas efter att barnet tvingats jobba på ett visst sätt med ekvationer (dock kan de tyvärr ha fördomar mot geometri också). Så passa på och sätt dina elever (och dig själv) i situationer, där du inte har någon aning om hur man löser problemet. Du får då vara kreativ och kommer förmodligen att komma på ett lättare sätt att hantera uppgiften än vad någon annan skulle ha berättat för dig.
Pythagoreiska tripplar i form av areor, del 4
I föregående del avslöjade vi processen med vilken vi kan förstora koordinatsystem på så sätt att de förstorade ciklarna innehåller icke-primitiva pythagoreiska tripplar.
Om ett heltal kan representeras som en summa av två kvadrater, så kan vi alltid förstora primitiva pythagoreiska tripplar med detta heltal. Till exempel är 5 = 1+4 = 12+22, alltså en summa av två kvadrattal. Rita då nya rutor (gå 1 steg åt ett håll och 2 åt ett annat) i det gamla koordinatsystemet, rutorna kommer ha area 5. Det betyder att alla areor kommer vara exakt 5 gånger större!
Hur är det med andra förstoringen av primitiva pythagoreiska tripplar, till exempel med faktor 3? Låt oss bevisa att trippeln (9,12,15) inte kan uttryckas i form av rektangelareor på en och samma cirkel. Specifikt undersöker vi hur rektangeln med arean 9 kan se ut.
Givetvis kan det vara en vanlig 3×3 eller 1×9 rektangel, där sidorna går längs med rutnätslinjerna. Men kan en rektangel med arean 9 ligga snett i rutsystemet?
Om en rektangelns ena sida ligger snett, så kommer rutnätspunkterna finnas på den med jämna mellanrum. Låt mellanrummets längd vara a. Vinkelrätt mot första sidan går rektangelns andra sida. Där hamnar rutnätspunkterna med exakt samma mellanrum. Eftersom rektangeln har sina hörn i rutnätspunkter, kommer alltså ena sidan består av k antal a:n och andra sidan av m antal a:n. Det vill säga k och m är heltal, medan a är roten ur summan av två heltalskvadrater.
Så arean på en sådan sned rektangel är k*m*a2, alltså en produkt av heltal. Det betyder att om k*m*a2=9, så är a2=1, 3 eller 9. Men varken 1, 3 eller 9 kan skrivas som summa av två positiva heltalskvadrater. Därför finns det inga sneda rektanglar med arean 9.
Överlag måste alltså någon av areans delare kunna uttryckas som en summa av två positiva kvadrattal, för att det ska finnas en sned rektangel med denna area. Det är dessutom ett tillräckligt villkor.
Det betyder att endast två rektanglar har area 9. Rektanglarnas mittpunkt sammanfaller med den omskrivna cirkelns, vi har alltså två varianter.
Men den första cirkeln innehåller bara en enda rektangel, medan den andra innehåller den primitiva pythagoreiska trippeln (9, 40, 41) och inga andra rektangelareor. Så trippeln (9,12,15) går inte att konstruera på det här sättet!
Så vi har hittat minst en trippel som inte är konstruerbar på det här sättet. Jag vet fortfarande inte om det är så att alla icke-primitiva tripplar med en faktor, som inte är en summa av två kvadrater, är okonstruerbara. Kanske kan du hitta ett motexempel?
Men denna fortfarande öppna fråga avslutar vi den här serien inlägg om pythagoreiska tripplar i form av areor. Läs gärna serien från början, kanske upptäcker du nya idéer när du läser för andra gången!
Pythagoreiska tripplar i form av areor, del 3
I del 2 såg vi att en primitiv pythagoreisk tripplel alltid kan representeras i form av rektangelareor (inuti rutnätscirklar).
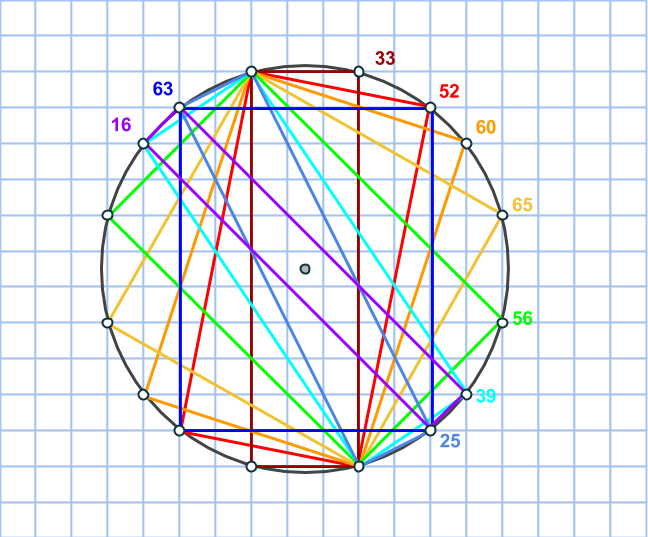
Dyker det upp exakt 3 olika rekatngelareor inuti en sådan cirkel?
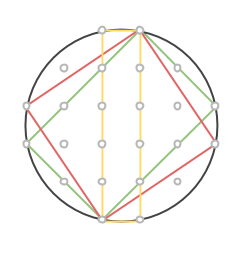
Nej, det kan dyka upp fler än så, vilket beror på att vi kan hitta cirklar där fler än 8 rutnätspunkter hamnar på cirkeln. Nedan ser ni nio olika rektanglar, med areor utskrivna, som vi kan hitta i en cirkel med 16 rutnätspunkter på randen. (Vad tror du förresten är det största antalet rutnätskpunkter man kan hitta på en cirkel?)
Men hur gör man med icke-primitiva Pythagoreiska tripplar? Konstruktionen från förra delen fungerar inte, eftersom icke-primitiva tripplar kan inte genereras på samma sätt från m och n som primitiva.
En icke-primitiv trippel är däremot lika med en primitiv, multiplicerad med en faktor, som till exempel (6,8,10) är trippeln (3,4,5) multiplicerad med faktorn 2. Om vi på något sätt kunde förstora alla rektanlar med faktorn 2, utan att förlora rutnätsegenskaperna, så skulle problemet vara löst. Men förstorlingen av alla rektanglar med faktorn 2 skulle ske om alla sidor förstorades med faktorn √2.
Detta kan vi göra om vi helt enkelt förstorar hela rutnätet med faktorn √2! Vi gör det genom att rotera koordinataxlarna 45 grader och betrakta fyra punkter som bildar en kvadrat med sidan √2 som en enda ruta. På bilden nedan är det nya rutnätet ritat i rött ovanpå det gamla (eftersom vi trots allt använder det gamla för att rita ut cirklar).
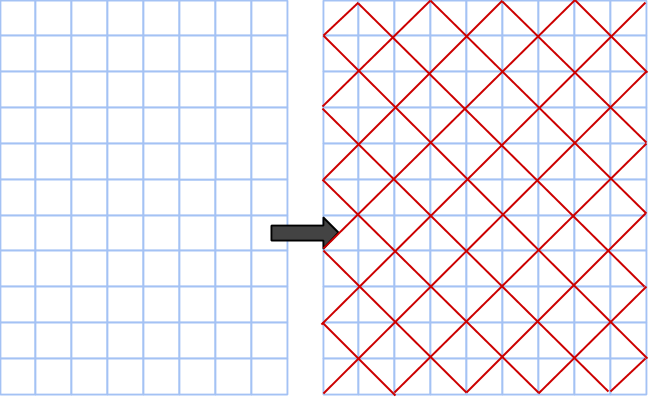
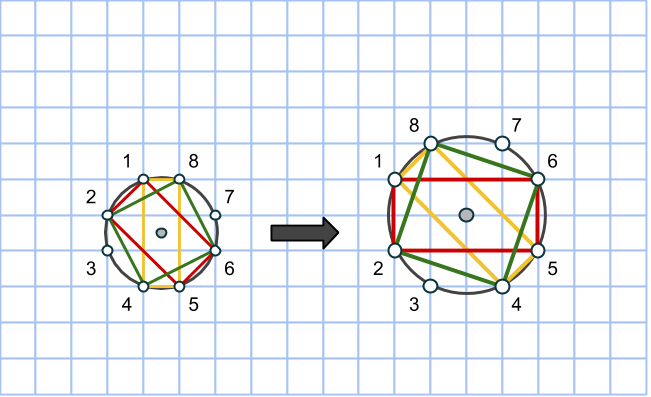
Vi gör samma sak med rutnätscirkeln: rotera och förstora med faktor √2, då bildar från en cirkel med areorna (3,4,5) en annan cirkel med rektangelareorna (6,8,10). Punkterna på cirkeln numreras för det ska gå lättare att se rotationen.
Men såklart kan vi bilda nya rutsystem på andra sätt och med andra rutstorlekar! Bland annat går att att förstora alla areor med 5, med 13 och såklart med produkter av faktorer, som vi redan kan förstora med. (Försök att hitta ett rutsystem med rutlängderna √5). På så vis går det alltså att konstruera alla icke-primitiva taltripplar på formen t.ex. (5*(m2-n2),5*2*m*n,5*(m
Men går att förstora på så sätt med alla faktorer? Går det till exempel att konstruera den icke-primitiva trippeln (9,12,15)? Vi besvarar den här frågan i den sista delen.
Pythagoreiska tripplar i form av areor, del 2
I del 1 såg vi hur vissa pythagoreiska tripplar kunde representeras i form av areor på rektanglar inuti cirklar på rutnät. I den här delen undersöker vi huruvida detta är möjligt för alla primitiva tripplar.
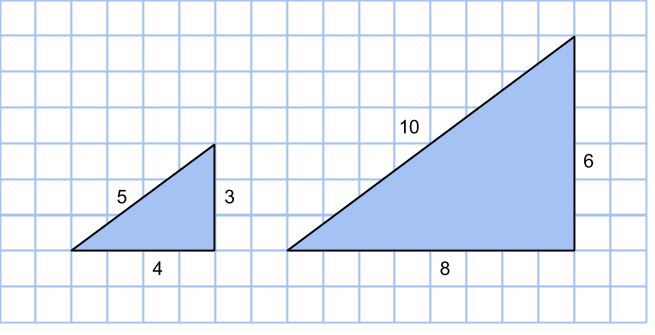
Primitiva pythagoreiska tripplar (a,b,c) är sådana att talen a, b och c inte har några gemensamma delare. Till exempel är (3,4,5) en primitiv pythagoreisk taltrippel, medan (6,8,10) är en icke-primitiv sådan.
Ur varje icke-primitiv pythagoreisk taltrippel kan vi nämligen få en primitiv: Om de tre talen har största gemensamma delaren d, så kan de skrivas på följande sätt: a = d·r, b = d·s och c = d·t.
Eftersom a2 + b2 = c2, så är även (dr)2 + (ds)2 = (dt)2. Förkortar vi likheten med d2, så får vi r2 + s2 = t2. Således har vi fått en ny pythagoriesk trippel (r,s,t). Den är primitiv, eftersom r, s och t inte kan ha några gemensamma delare (deras gemensamma primfaktorer skulle ha ingått i d).
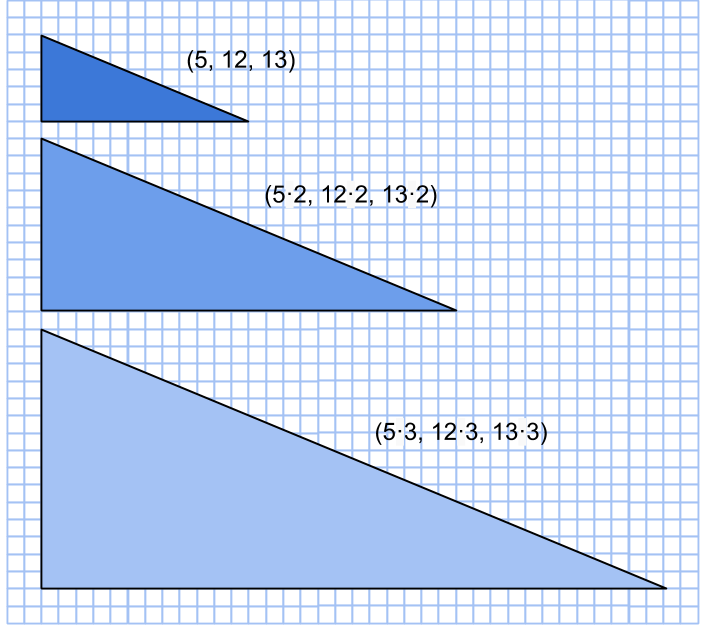
Ur primitiva taltripplar kan man förstår tvärtom få oändligt många icke-primitiva genom att multiplicera alla tre talen med en och samma faktor.
Således finns det oändligt många pythagoreiska taltripplar, men finns det oändligt många primitiva?
Ja, det visar sig att det finns oändligt många sådana och dessutom genereras varje primitiv trippel genom två heltal, som vanligen betecknas m och n. Dessa tal bör vara relativt prima och ett av dem måste vara udda, medan det andra måste vara jämnt. Givet sådana två tal, kommer följande tre tal bilda en pythagoreisk trippel: (m2-n2, 2mn, m2+n2). Kontrollera gärna att oavsett vad m och n är, så kommer Pythagoras likhet gälla för dem.
Till exempel kan trippeln (3,4,5) skrivas som (22-12, 2·2·1, 22+12), det vill säga den genereras av talen 1 och 2.
Talen 3 och 8 ger oss trippeln (2·3·8, 82-32, 82+32), det vill säga (48, 55, 73) och just för det exemplet kommer vi rita upp en cirkel som innehåller rektanglar med respektive areor. Men låt oss beskriva hur vi agerar för allmänna m och n, det vill säga för en godtycklig primitiv pythagoreisk taltrippel.
Talen m och n är nämligen till stor hjälp när cirkeln konstrueras. Vi börjar inte i cirkelns mittpunkt, som man skulle kunna tro, utan på en punkt på randen (en heltalspunkt, som kommer vara hörn för åtminstone en rektangel). Markera en punkt m+n steg nedanför startpunkten, samt m-n steg till höger. Komplettera till en rektangel med en fjärde punkt på rutnätet. Rektangelns area är (m+n)(m-n) = m2 – n2 och dess mittpunkt måste sammanfalla med cirkelns. Vi bestämmer den genom att korsa diagonalerna.
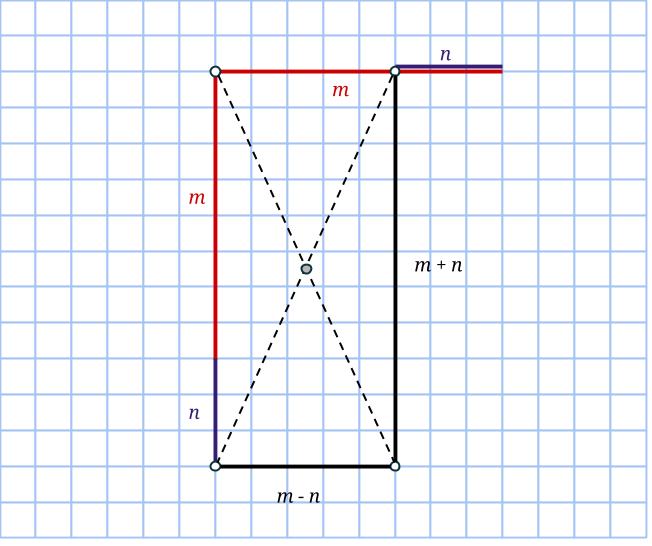
Rektangeln vi har ritat är uppenbarligen inte en kvadrat, så vi får fyra nya rutnätspunkter som också ligger på cirkeln genom att rotera rektangeln 90 grader runt cirkelns mittpunkt:
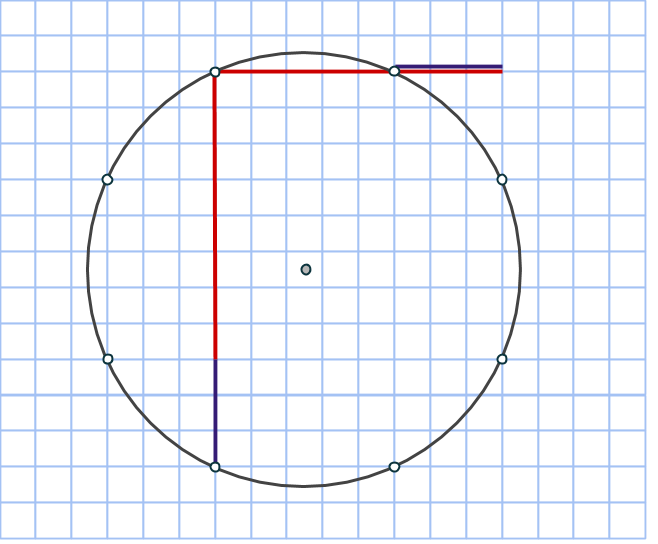
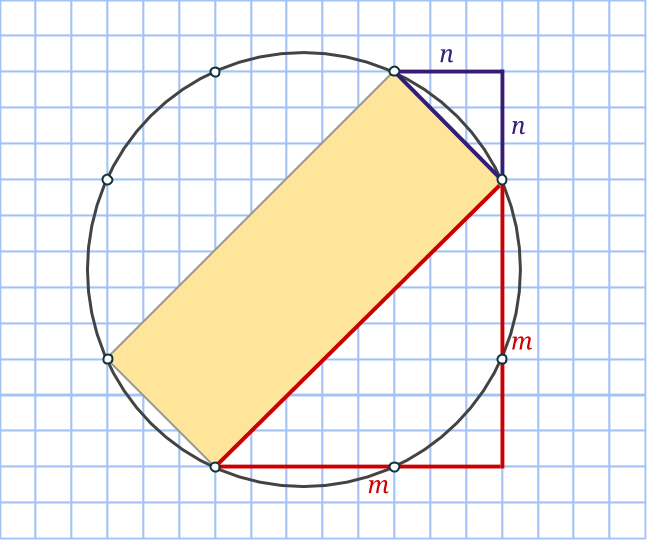
Nu har vi fått en cirkel med åtta rutnätspunkter utsatta och det är faktiskt allt vi behöver! Låt oss bevisa det.
Markera en rektangel som har sina sidor vinklade 45 grader i jämförelse med den första. Kortsidan utgör hypotenusan i en likbent rätvinklig triangel med sida n, medan långsidan är på samma sätt, fast med m. Då kommer alltså arean att vara √(2n2)·√(2m2) = √(4m2n2) = 2mn. Precis som ett av talen i den pythagoreiska trippeln.
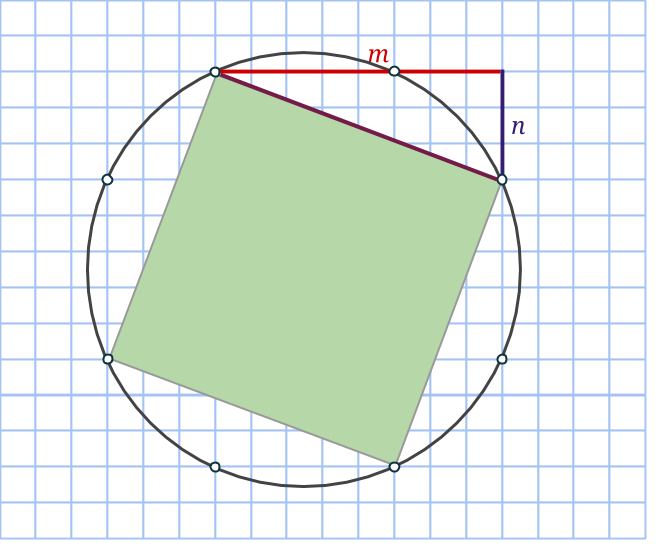
Markera nu en rektangel, som dessutom är en kvadrat genom att ta varannan punkt på cirkeln. Sidan blir lika med √(m2+n2), så arean måste bli lika med just m2+n2. Därmed är den sista arean funnen!
Nu uppstår det fler frågor: Dyker det någonsin upp några extra rektanglar med en annan area vid en sådan konstruktion? Och hur gör man för att konstruera cirklar för icke-primitiva pythagoreiska taltripplar?
Vi försöker besvara dessa frågor i nästa del.
Pythagoreiska tripplar i form av areor, del 1
[kkratings]
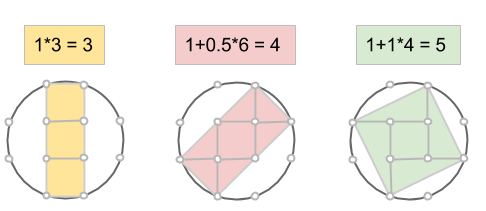
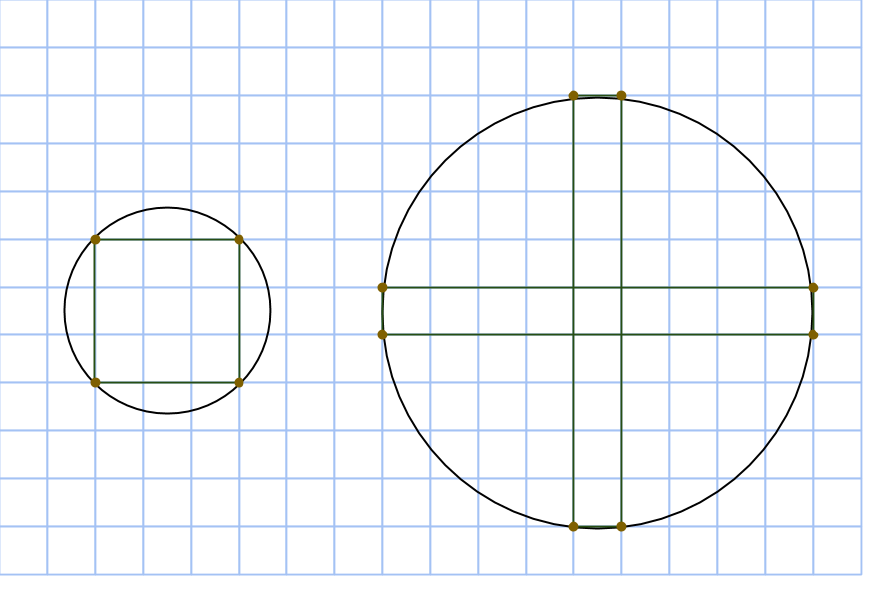
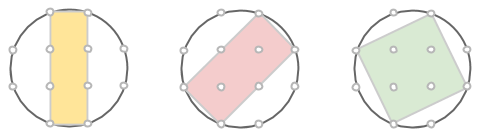
Föreställ dig ett rutnät av punkter. Det går att hitta massvis med cirklar som går igenom några av punkterna. En av de minsta sådana cirklarna har hela 8 punkter på sin rand:

Det går även att hitta några rektanglar inuti sådana cirklar, som har alla sina hörn i punkterna på cirkelns rand (notera att även kvadraten räknas som en rektangel). Kan du bestämma rektanglarnas areor?
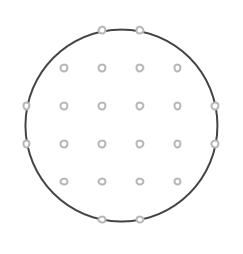
Kan du på samma sätt i cirkeln nedan hitta rektanglar med areorna 5, 12 och 13?
Följande fråga uppstår: går det att hitta vilken Pythagoreisk trippel som helst på samma sätt?
Kryssa grannrutor
Kryssa grannrutor
[kkratings]
Chiyen satte ett kryss i en ruta på en rektangel. Esteban får sätta kryss i de andra rutorna, men bara om de uppfyller följande regel: man får bara kryssa i rutor som har ett udda antal grannrutor med kryss (med grannrutor menas de som delar en sida med rutan).
Kan Esteban kryssa i alla rutorna på rektangeln, oavsett vilken ruta som blev ikryssat av Chiyen, om rektangeln har storleken:
(a) 8×9 rutor?
(b) 8×10 rutor?

Uppdelad rektangel
Uppdelad rektangel
[kkratings]
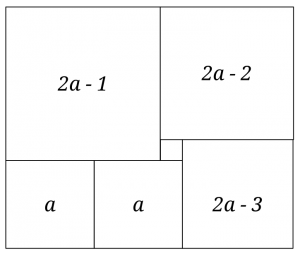
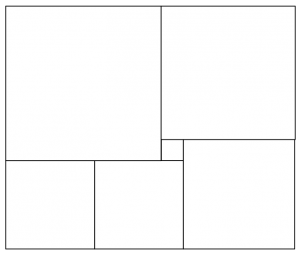
En rektangel är uppdelad i 6 kvadrater (se bilden nedan). Hur stor är den största kvadraten om den minsta har sidlängden 1cm?
Obs! Figuren är inte nödvändigvis perfekt, därför räknas det inte som en lösning att mäta längderna.
Rektangel
Rektangel
[kkratings]
Du har tillgång till 12 sträckor som är 2cm långa, 12 sträckor som är 3cm och 11 sträckor med längden 5cm. Går det att bygga en rektangel av alla sträckorna med sidlängderna lika med ett helt antal centimeter?
Lösningen till problemet för de äldre vecka 45
Mattegåta
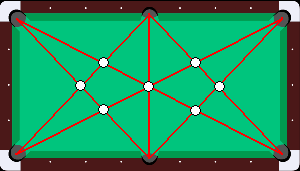
Ett biljardbord har en långsida som är dubbelt så lång som kortsidan. I varje hörn finns det ett hål, samt två hål till finns på varje långsidas mitt.
Vilket är det minsta antalet bollar som man kan placerat ut på bordet så att varje hål befinner sig på samma linje som ett visst par av bollar? (Bordet är rektangulärt, hål och bollar antas vara lika stora som punkter.)
Diskussion
Eftersom det frågas efter det minsta antalet i uppgiften är det underförstått att resultat skall bevisas. Det vill säga det måste finnas ett exempel med x bollar (om x är svaret), samt bevis för att det inte går med färre än x bollar.
Ett sätt att jobba på är att börja underifrån (till exempel med 1 eller 2 bollar) och för varje antal antingen visa att det inte går eller att det går. Fallen är oftast svårare närmast svaret. Lite som i fyrfärgsproblemet!
Fyrfärgsteoremet
Sats. För en platt ”karta” räcker det alltid med fyra färger för att måla ”länderna” på kartan så att inga två länder med gemensam gräns har samma färg (gränser utgörs av raka eller krokiga linjesegment).
Det var länge känt att det räckte med fem färger och att det finns kartor som inte går att färga med tre färger. Men fallet fyra tog lång tid tills den äntligen bevisades med hjälp av datorberäkningar.
Lösning (av Erik Svensson)
Till att börja med kan vi uppenbart utesluta att det går med bara en boll (och förstås även med noll bollar).
Det finns ej heller någon lösning för två bollar, ty vi vet att två bollar (punkter) entydigt bestämmer en linje, så om samtliga hål ska ligga i linje med två bollar, då måste alla hålen ligga på samma linje. Men hålen på biljardbordet ligger inte på en linje.
Det är inte heller möjligt med tre bollar, vilket vi ser om vi försöker konstruera en. Om vi har tre bollar, då finns det två möjligheter: Att de ligger på en linje eller att de inte gör det.
Ifall de ligger på en linje, då får vi en motsägelse med samma resonemang som för två bollar, och ifall de inte ligger på en linje så bildar de en triangel. I så fall utgör varje linje med två bollar en sida i denna triangel, och bollarna är hörnen.
Vi börjar med att konstatera att ingen sida i denna triangel kan täcka tre hål, ty de enda linjerna på bordet som täcker tre hål är långsidorna. Ens om vi antar att frågeformuleringen tillåter bollar längs med sidorna innebär detta att två bollar måste ligga på en av långsidorna, vilket innebär att den tredje bollen måste ge upphov till två linjer som täcker samtliga tre resterande hål, vilket medför att någon av dessa två linjer måste täcka två hål på den andra långsidan och ändå korsa den första långsidan, vilket är omöjligt.
Att täcka fyra eller fler hål med en linje är förstås också omöjligt som biljardbordet är uppbyggt.
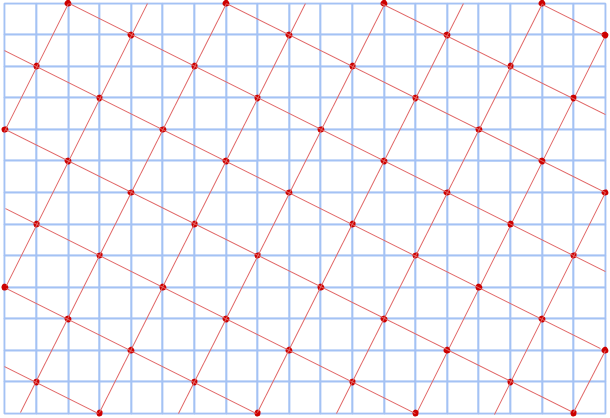
En linje kan ej heller passera genom bara ett hål, eftersom detta lämnar fem hål att täckas med de resterande två linjerna, och alltså måste någon av dessa linjer täcka minst tre hål, vilket motsäger det vi just kom fram till. Även en linje som inte täcker några hål kan vi utesluta, eftersom denna linje i så fall kan tas bort och därmed ge en lösning för två hål, vilket vi visat inte existerar.
Således måste vi ha tre linjer som täcker exakt två hål, och de måste täcka två bollar vardera. Eftersom varje boll är ett hörn i den triangel som bildas ligger varje boll på två sådana linjer.
På bilden ser vi alla möjliga linjer som täcker två hål, samt alla skärningspunkter mellan dem. Dessa punkter är de enda kandidaterna till var en boll kan ligga. Vi ser emellertid att det inte finns någon triangel av sådana punkter (med de utmarkerade linjerna som sidor), och den minsta slutna figur vi kan bilda är en fyrhörning. Alltså finns det ingen lösning för tre bollar, men det finns en för fyra, till exempel genom att välja fyra punkter som bildar en fyrhörning i bilden och lägga bollarna där.