Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.
Här kan du se vad vi tidigare har gått igenom.
Former
Topologi handlar om olika slags former hos objekt. Båda barn och vuxna har bra intuition för former och hur de kan förändras, men ibland kan ointuitiva saker också hända:
Denna lektion skall vi experimentera med form hos olika sorts objekt med olika material.
Lera
När man ska förklara ordet topologi för någon som inte vet vad det är, så illustrera man ofta med detta exempel.
Man säger att en munk och en kopp är topologiskt sett samma, eftersom man kan omforma dem till varandra på ett naturligt sätt, om de nu skulle vara gjorda av modellera.

Lera är precis vad vi kommer pyssla med. Alla barn får var sin bit lera (t.ex. får alla var sin färg) och får i uppgift att tillverka en kopp med öra. Kan de göra det utan att riva leran någonstans? (Ńej, det kan de inte, så de får riva den här gången.) Kan de nu göra om koppen till en ring/en munk utan att riva leran? Det är tillåtet att klistra ihop leran, annars blir detta en väldigt opraktisk uppgift. I topologin får man egentligen inte klistra två punkter hur som helst om objektet ska behålla den topologiska formen.
Metalltråd
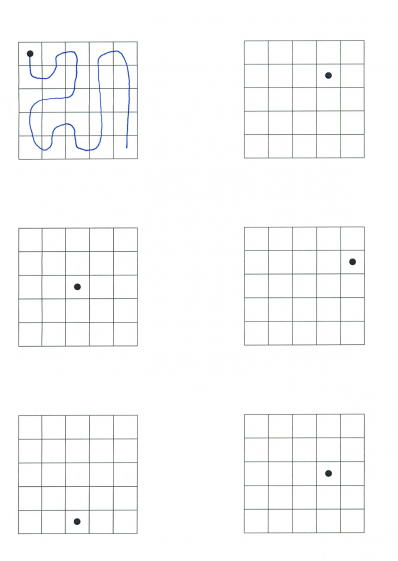
Även platta objekt kan vara topologiskt ekvivalenta eller inte. Till exempel kan siffrorna 1, 7 och 5 omformas till varandra, medan 9 och 6 tillhör en annan grupp. Skillnaderna är lättast att se om man tillverkar siffrorna i böjbart material, t.ex. snöre eller ståltråd och tydlig markerar platsen där materialet träffar sig självt igen (som i mitten på siffran 8).
Barnen får som första uppgift att på en bit ståltråd göra så många siffror den kan i rad. Början kommer att se ut ungefär så här:

Det viktiga är att tråden ska gå att räta ut igen!
Efter att barnen upptäcker att bara siffror 1,2,3,5 och 7 går att göra på det här sättet diskuterar vi hur det ligger till med andra siffror och sedan också bokstäver. Vilka stora bokstäver är till exempel i samma grupp som A?
(Svar: R)
Detta påminner om en gåta som folk länkar till då och då. Jag tror att det kan stämma att för mycket matematikutbildning skadar om man ska lösa gåtan fort:
8809 = 6
7111 = 0
2172 = 0
6666 = 4
1111 = 0
3213 = 0
7662 = 2
9312 = 1
0000 = 4
2222 = 0
3333 = 0
5555 = 0
8193 = 3
8096 = 5
7777 = 0
9999 = 4
7756 = 1
6855 = 3
9881 = 5
5531 = 0
2581 = ?
Knutar
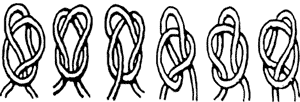
Barnen får två snören var för att experimentera med knutar. Först får de försöka knyta enligt schema, som denna knut:

Sedan gäller det att först gissa utifall bilden ger oss en knut eller inte utan att försöka göra knuten själv. Har man en gissning får man prova att bevisa det med hjälp av sitt snöre.
Flätor
Knutar är ganska enkelt för större barn, så de får gå vidare till flätor. Det finns förstås den vanliga flätan, som man gör med tredelat hår. Men det är inte bara den vi ska experimentera med.
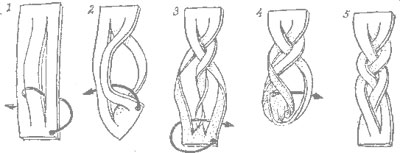
Även fyra delar kan ge en fläta:
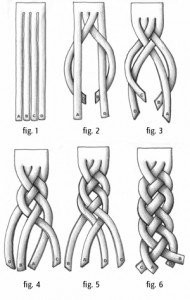
Och fem förstås:
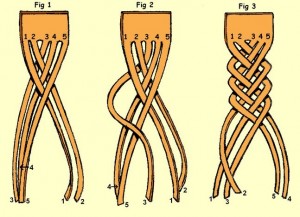
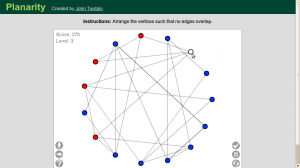
Uppgifter utan ord
Jag är alltid mycket för den visuella matematiken. En bild säger verkligen mer än tusen ord. Uppgiften nedan som vi avslutar med (den har inte så mycket med topologi att göra) kommer ursprungligen från inläggetMath without Words.