Universitetsmatte – Mattebloggen

Matematik i Genikampen – andra avsnittet

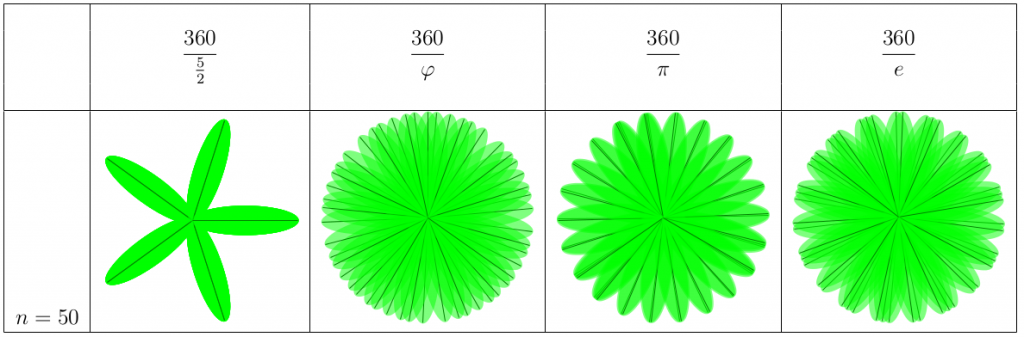
Andra avsnittet innehöll kanske inte lika mycket matte som första avsnittet, men det betyder ju inte att man inte skulle vara smart för att klara tävlingarna. Och allt som har med kreativt tänkande att göra kan jag om jag vill koppla ihop med matte så nu tänker jag göra det.

Flottbygge: Planering och materielinköp

Vi fick 3000 kronor för att handla materiel till vår flotte. Tävlingsledarna skulle kopiera både gula och blå lagets inköp och lagen skulle få de andras inköpta material först. Men i andra omgången skulle lagen få eget material, så det gällde att inte köpa sjukt dåliga saker. Framförallt gällde det att köpa något som man själv skulle ha mer nytta av än motståndaren i samma situation.

Enligt tävlingsreglerna behövde man antingen vinna båda omgångarna för att vinna hela tävlingen eller vinna en av omgångarna med bäst vinsttid (det vill säga, bara tiden för den vinnande omgången räknades). En grej som är lätt att se i efterhand och lite svårare att tänka på innan tävlingen är att det är bara den andra omgången som spelar roll. Givet erfarenhet och att man bygger med eget material tar den andra omgången med störst sannolikhet kortare tid för båda lagen. Det gällde alltså att samla erfarenhet i första och ge järnet i andra omgången.

Under tidspress kunde vi inte vara så värst smarta och planerade en konstruktion som skulle bli alldeles för tidskrävande i andra omgången (så den övergavs). Inne i affären fokuserade vi på att göra beräkningar av typen ”hur mycket volym måste flotten ha för att bära allas vikt?” (blå laget räknade detsamma verkar det som). Fysik i all ära, men ingenjörskonsten med höftning snarare än exakta beräkningar tar ändå alltid priset när det är snabba puckar och inte forskning som gäller.

Andra beräkningar som vi kunde göra skulle då vara hur många hinkar sand flotten skulle kunna bära (förutom oss själva då). Jag kom tyvärr inte ihåg att vi hade fått hinkmått eller mått på lådan vi skulle fylla också, så jag fokuserade på att räkna på kostnaden istället. Tog lite i överkant på varje vara för att inte hamna över (samt för att räkna snabbt) och det slutade med att vi verkligen inte hamnade i överkant, utan hade kunnat köpa typ ett halv toasits till.

Att köpa toasitsar som åror var en briljant idé utav Nina som sparade gula laget mycket tid som annars skulle behövs till åror-tillverkning. Synd att de var så dyra!

Flottbygge: Första omgången

Första omgången gick för båda lagen ut på att samla erfarenhet, framför allt om en bra form på flotten samt om hur många omgångar fram och tillbaka som skulle behövas för att fylla lådan med sand. Vi hade nio hinkar tillgängliga, om jag minns rätt (dock sänkte vi i gula laget en hink i sjön i första omgången). Gula laget hann dumpa sand två gånger, medan blå fyllde hinken på tre gånger! Det betydde att två eller tre gånger skulle behövas i andra omgånger för att vinna hela tävlingen.

Om man skulle åka två omgångar långsamt istället för tre snabbt skulle man ändå vinna tävlingen då tiden att åka fram-tillbaka-fram är tre intervall, medan fram-tillbaka-fram-tillbaka-fram är fem intervall, alltså tar det andra fallet mer än 50% mer tid än det första, om man nu åker med samma hastighet. Tiden det tar att dumpa sand är försumbart i jämförelse med tiden det tar att åka. I programmet hör man att vinsttiden är mer än femtio minuter. Skulle gissa på att max 15 min gick ut på att bygga för blå laget, medan allt annat var rodd (i snitt 7 min per sträcka fram eller tillbaka).

Flottbygge: Andra omgången

Vi i gula laget satsade på att fylla lådan på två rundor, det vill säga åka fram-tillbaka-fram och vinna. Blå laget satsade på samma sak. Viktiga skillnaden för gula laget var att istället för att lägga de 12 frigolitbitarna i fyra lager lägga dem i tre lager. Det betyder att flotten blev till ytan större (4 plattor iställer för 3) och mer stabil (lägre). Det var helt klart den största förbättringen för gula laget gentemot första omgången. En eloge till blå laget som körde på den utformningen av talet 12 redan från omgång ett! I slutändan som det syns i avsnittet var det inställning och småsaker som avgjorde och inte matten. Men utan de idéer som jag nämnt skulle det gula laget varit körda. Tur att det är hög lägstanivå på lagen, så att det inte blir jätteskämmigt när vi spelar genier!

Laser och speglar

Andra tävlingen gick ut på att rikta en laserstråle med hjälp av speglar. Strålen skulle förbi en massa hinder och träffa en ”prisma” (jag tyckte det mera såg ut som en halvklot ihopsatt med en halvikosaeder eller nåt, en prisma ska ha två kongruenta parallella sidor vad jag vet). Tävlingen gick i omgångar; varje omgång bestod av en planeringsfas och en resultatfas. Under planeringen fick man mäta på banan, ställa om och flytta på speglar, göra eventuella beräkningar. Sedan fick man se laserstrålen tändas och en person fick springa fram och göra högst en markering på banan.

Detta syns inte i tv men tävlingen tog hela 14 (!) omgångar. Första omgången träffade gula laget sin första spegel, medan blå laget gjorde inte ens det. Till andra omgången flyttade vi i andra laget andra spegeln lite för att strålen skulle träffa den, men tydligen flyttade vi den lite för mycket! Det var bara på tredje omgången som andra spegeln blev träffad. Och detta var bara speglarna i början, som sattes ut på samma höjd allihopa och med enklar vinklar på 45 grader. Om det var så små marginaler på dem skulle spegelinställningarna i tre dimensioner bli exponentiellt mycket svårare!

Vilket de också blev. Beräkningarna kunde man kasta i papperskorgen och vårt lags strategi var att köra på empiri, det vill säga testa och sedan göra små ändringar. Sedan kan man göra empiri olika bra ocskå. Säg att du ska gissa ett tal mellan 1 och 100 och får veta om din gissning är mindre eller större än det korrekta talet. Då är det bäst att fråga om talet 50 (eller 51). Om det tänkta talet är större, frågar du om 75 och så vidare. På liknande sätt var det för oss när vi ställde in spegelvinklar (både plattformens vinklar och spegelns vinkling): Börja med en gissning, gå sedan ganska långt åt andra hållet (för att definiera en gissningsintervall), sedan någonstans i mitten om man ser att den korrekta vinkeln är mellan de två gissningar, sedan fokusera på rätt halva av intervallet för att få rätt fjärdedel och så vidare.

Detta funkar bra med småvinkeländringar, eftersom, som jag säger i programmet, ”sinus är linjär vid 0”. Det kommer från att
$\lim_{x\to 0} \dfrac{sin x}{x} = 1$ .

Och då även
$\lim_{x\to 0} \dfrac{tan x}{x} = 1$ .

Om markavståndet (dvs avståndet projicerat ovanifrån) från spegelns mittpunkt till nästa spegel är given, så kommer alltså vinkeln bero linjärt på avståndet i den andra ledden (just det vi försöker gissa). Dubblas vinkeln, så dubblas avståndet alltså.

Så för små vinklar funkar det då med samma genomsökningsstrategi som med talen från 1 till 100. T.ex. testar vi med 5-graders vinkeln, sedan med 7 och om strålen ska vara däremellan testar vi med 6 grader (istället för att vara smarta och försöka beräkna att vi ”borde” testa 6,5 eller nåt sånt). Sånt kan ”inte ens jag” beräkna snabbt utan miniräknare och dessutom är det massa felmarginaler på mätningar, så det hade varit meningslöst ändå.

Vi fick instruktioner om att skriva lite smarta saker på tavlan, speciellt under första omgången. Det finns inte jättemycket att skriva när man kör på empiri annat än små anteckningar, så vi roade oss lite istället:

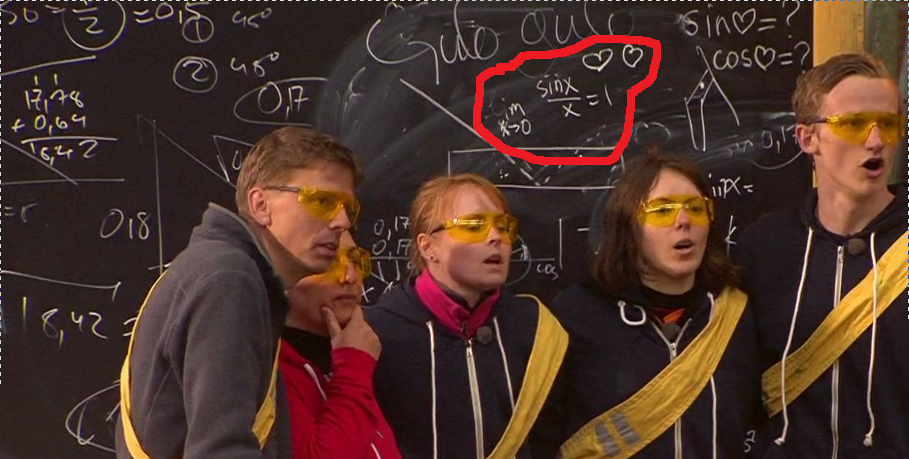
Så klart fanns det annat att tänka på än att bara höfta och ändra inställningar. En viktig sak är hur många speglar man bestämde sig för att använda (man behövde inte använda alla). Ju färre speglar, desto färre lyckade steg man behövde göra. Men å andra sidan skulle varje steg vara något svårare om man skulle försöka ställa in speglarna i 3D (vi kunde ju inte ställa de var som helst, utan bara på några av hindren). Vi körde på strategin ”better be safe than sorry” och jag blå laget gjorde det också, det vill säga använda många speglar med mindre avstånd/svårighetsgrad mellan varje intilliggande par.

En annan sak som jag kom på och var ganska stolt över var att använda flera av de lediga speglarna att ställa på rad för att chansa på att strålen skulle råka träffa nästa spegel också. Lasern bana var mycket värdefull att se och får man se ett steg till ”gratis” var det mycket värt.

Blå laget körde på att titta i speglarna och försöka se prisman i första spegeln. I programmet är jag skeptisk till hur de kunde låta ögat vara så stabilt, men det funkade ju hyfsat bra för dem. Så kanske är det en hållbar strategi ändå! Problemet är att med många speglar multipliceras felet för varje steg. Tänk på när du är i ett rum med massa speglar. Om du flyttar ögat, flyttar de mer avlägsna spegelbilderna mycket snabbare!

Svår tävling var det och krävde mycket tid och energi. Men det var nog min favorittävling i hela Genikampen. Jag gillar att lösa problem när man har ganska god tid på sig. För varje steg fram man kommer får man en kick och vill fortsätta. Dessutom kan man komma på fler och fler strategier som kan testa och föra en fram bättre och snabbare!

Pentago

Duellen gick ut på att spela några omgångar av spelet Pentago, bäst av tre. Duellanterna fick veta reglerna lite innan och provspela ett par gånger. Det finns ju stor risk för missuppfattning, även när man kommunicerar med oss genier ;) Det vore tråkigt om någon gjorde ett olagligt drag i tv eller nåt, även om det såklart svårt att göra det i just det här spelet.

Som i många spel med ett litet spelplan finns det redan beräknat hur man ska spela optimalt. I det här fallet har första spelaren en vinnande strategi, detta behövde dock beräknas med hjälp av en superdator! I massa andra sådana spel är det bevisat att första spelaren har i alla fall en icke-förlorande strategi, som t.ex. ~~i schack (vit kan aldrig förlora om hen gör rätt!)~~ i ”fem i rad” på ett oändligt bräde, men i många sådana spel finns det så många möjligheter att man inte har räknat ut den konkreta strategin. Pentago är rätt litet så det går att beräkna.

Testa att spela och vinna Pentago

Frågan är om man kan lära sig den vinnande strategin utantill, det har jag ju inte försökt mig på. Även om datorn kan göra det på några sekunder, kanske kan det ta en människa veckor för att ”plugga öppningar”. Det hade inte duellanterna. De hade kunnat fokusera på att plugga hur man ”inte gör fel”, t.ex. att man inte ska lägga i hörnen som första spelare och hur man i så fall ska svara som andra spelare. Men jag tror inte det skulle ha hjälpt för att garanterat vinna. Jag tror man kan jämföra Pentago med Othello: Det tar ett tag att bemästra och att lära sig se mönster, men när man väl gjort det så kan man spöa vilken nybörjare som helst. Det var skönt att duellanterna inte hade spelat spelet förut, så att de tävlade på samma villkor.

Jag och Axel fick senare låna spelet och vi försökte komma fram till en vinnande strategi ”för hand” genom att testa olika möjligheter, men jag tror inte vi hann göra det på en halvtimme :)

Matteskämt

Skämtet är till för en bred grupp läsare som har läst homologisk algebra:

banan-split-exact_large

Förklaring
Skämtets skapare: Sebastian Öberg

Sitter du som läsare på några bra/dåliga matteskämt? Skriv gärna i kommentarerna!

Phi-växter, pi-växter och e-växter, del 2

I del 1 kom vi fram till att en växt inte bör växa med en rationell vinkel. Det vill säga, om vinkeln bladen emellan är 360/(p/q), så kommer växter sabba solljuset för sig själv efter p blad.

Om p=5 och q=2 så växer bladen ut med 360/(5/2)= 144 graders mellanrum. Det innebär att nya blad sprutar ut 144, 288, 432 (det vill säga 72), 216 graders mellanrum i förhållande till det första. Men nästa blad, det sjätte, kommer hamna 360 grader ifrån det första, det vill säga på exakt samma ställe! Detta är väldigt ooptimalt för en växt.

Oavsett vad för rationellt tal vi tar kommer samma elände att hända efter p blad, eftersom då har bladen avlagt 360/(p/q)*p = q*360 grader, alltså ett helt antal varv. Växten vill att det aldrig riktigt ska bli helt.

Så händer det inte med de irrationella talen. Låt oss jämföra vad vi får för irrationella växter. I tabellen ser du en rationell växt, en phi-växt, en pi-växt och en e-växt. Början ser det relativt likt ut emellan alla växterna:

Men efter fem blad har den första växten fördelat sina blad jämnt, medan de andra ser annorlunda ut. Phi-växten har fördelat sina blad ganska bra, medan pi-växten har sina blad onödigt trångt.

Vad händer vid 12 blad? Oförändrat för den rationella växten – den kan bara ha sina blad på 5 positioner. Phi-växten är jämnfördelad som vanligt, e-växten är också ganska bra. Pi-växten har däremot tre tydliga delar. Kan det ha att göra med att pi på ett ungefär är lika med 3?
n12

Vi 30 ser vi hur växterna klarar av många blad. De mörkare partierna visar på att bladen överlappar varandra, vilket sker mer och mer på e-växten och pi-växten speciellt. Överlappningen finns hos phi-växten också, men den är mer jämnfördelad. Notera att pi-växten har 22 tydliga delar!
n30

Till sist kollar vi riktigt många blad, 50. Pi-växten har 22 väldigt tydliga delar, e-växten har 19, medan phi-växten aldrig har två blad så pass nära varandra som de andra växterna. Den verkar ha 5 stora delar, vilket tyder på att vi i verkligheten skulle se 5 spiraler för den bladstorleken.
n50

Varför blir det 22 tydliga delar hos pi-växten? Det har att göra med att pi approximeras väldigt bra med talet 22/7 (ca 3,14), vilket får växten att agera som en vanlig rationell växt och överlappa sina egna blad efter 22 stycken. Varför är vissa växter ändå pi-växter, som vi såg i förra delen? Jag gissar på att många verkliga plantor inte har så många blad eller grenar, och därför spelar det inte så stor roll för dem att det blir problem efter 22 stycken. De satsar snarare på 3 eller något sådant.

På samma sätt är 19/7 ett rationellt tal nära talet e (men inte lika när som 22/7 är pi), därför bildas det 19 delar på e-växter. Jag vet inte varför jag inte träffat på e-växter hittills, de verkar ju växa helt ok i början.

Men talet phi är väldigt speciellt. Det finns inte någon rationell approximation av det talet som är i någon mening så bra som 22/7 är för pi. Visst, vi kan använda större nämnare för att få ett rationellt bråk som är så nära phi som vi vill, men då blir nämnarna nästan onaturligt stora. För mer rigorös definition av bra rationella approximationer, se Hurwitz sats. Konstanten i satsen kommer just ifrån phi, det gyllene snittet, och det är det som medför att phi är det mest irrationella talet.

Det innebär att just den konstanten är optimal för växter med stort antal blad, frön, grenar etc. och det är därför vi vanligen finner just 34 och 55 spiraler på solrosor och inte 22 (Klicka på bilden för att räkna själv).

Phi-växter, pi-växter och e-växter, del 1

Hur kommer det sig att det finns spiraler på kottar, kronärtskockor och ananaser? Om du inte har sett förklaringen, rekommenderar jag Vi Harts videoserie ”Spirals, Fibonacci, and Being a Plant”: del 1, del 2 och del 3.

(Eller kolla upp en sida på svenska med många bra bilder.)

kotte

En av sakerna som avslöjs är att växternas blad växer ut med en och samma vinkel i förhållande till föregående bladet, nämligen vinkeln $\frac{360^\circ}{\varphi}$ , där $\varphi$ är det gyllenne snittet, även kallad det mest irationella talet. Detta för att bladen aldrig ska hamna direkt över och blockera solljus för varandra.

Eftersom bladen inte är hur tunna som helst, kommer de så småningom ändå överlappa varandra delvis. Därför bildas det spiraler, vilket förklaras i videorna. Men varför är antalet spiraler alltid lika med ett fibonaccital, för tallkottar oftast 5, 8 eller 13 (plocka upp en kotte och räkna spiralerna åt båda hållen)?

Min förklaring är att gyllene snittet approximeras med exempelvis 8/5, vilket betyder att växten efter 8 blad har avlagt $8\cdot\frac{360^\circ}{\varphi}$ grader, vilket är ungefär lika med $8\cdot\frac{360^\circ}{\frac{8}{5}}$ grader, det vill säga typ 5 varv. Och så med alla andra heltalsapproximationer, när växten
har gått ett ungefär helt antal varv, så har det vuxit ut ett fibonacciantal blad. När ett nytt varv börjar, bara då kan spiralerna börja växa, och därför är antalet spiral lika med antalet blad som vuxit ut hittills, det vill säga ett fibonaccital.

Vi sade förut att $\varphi$ var det mest irrationella talet. Vad ska det betyda? Alla irrationella tal är ju lika irrationella, men vissa tydligen mer irrationella än andra. För växten innebär det att det nya bladet dyker upp inte bara på en ledig plats, utan också på en plats där det finns som mest utrymme (jag vet inte riktigt hur detta ska förklaras matematiskt).

Men varför skulle inte en växt kunna växa med en annan irrationell vinkel, som exempelvis $\frac{360^\circ}{\pi}$ eller $\frac{360^\circ}{e}$ grader? Talet $\frac{22}{7}$ är ju en väldigt bra approximation av $\pi$ , så varför skulle inte en sådan $\pi$ -växt kunna ha 22 spiraler?

Nu när jag inte kan spekulera mer matematiskt, går jag ut i naturen och letar. De första två växter jag hittar verkar vara typiska $\varphi$ -växter, men den tredje har vinkeln närmare $114,6^\circ$ , det vill säga $\frac{360^\circ}{\pi}$ !

Eller nja, inte om man kollar på de färdigväxta bladen, då är det en vanlig $\varphi$ -växt:
SAMSUNG

Den här då? Det är lite svårt att se i vilken ordning bladen har växt ut.

SAMSUNG

Men om det är någon av våra förmodade vinklar, bladen emellan, så är det i alla fall $\pi$ :

SAMSUNG

Hurra! En $\pi$ -växt! Så inte alla växter följer $\varphi$ -lagen… Eller har jag mätt fel? Varför är de flesta växter ändå $\varphi$ -växter?

Kan du hitta andra irrationell växter i naturen, kanske med vinkeln $\frac{360^\circ}{\sqrt{2}}$ mellan bladen? Om en vecka kommer jag med mer spekulationer och förklaringar om växternas utväxtvinklar.

Bollvolymer i n dimensioner

Det är lätt att med experiment uppskatta volymer av olika tredimensionella kroppar: Exempelvis kan ett akvarium i from av en rätblock fyllas med vatten och sedan kan man mäta hur mycket vatten som gick åt. Samma kan göras med (ungefär) sfäriska behållare. Med matematik kan man bevisa att formeln för volymen av en tredimensionell boll är $\frac{4}{3}\pi R^3$ , vilket redan Arkimedes visade på den gamla goda tiden.

vatten_boll

Svårare är det när objekt har 4 eller fler dimensioner. Vi har inte längre några fysiska experiment vi kan göra, men för matematiken spelar det mindre roll hur många dimensioner det handlar om. Bollar i olika dimensioner är nämligen väldigt lika varandra om man tittar på dem med hjälp av ekvationer. Men låt oss börja från början.

Vad är en 1-dimensionell boll? Det är ju alla punkter på en linje, som ligger på ett givet avstånd från en given punkt eller närmare. Med andra ord, ett intervall. Om det givna avståndet, det vill säga radien, är lika med $R$ , så är intervallets längd lika med $2R$ . Det kan vi kalla formeln för volymen av en 1-dimensionell boll (väldigt fancy sätt att säga ”längd”).

En 2-dimensionell boll, som du säkert redan gissat, är en cirkel. På högstadiet (hoppas jag) lär man sig att cirkelns area är $\pi R^2$ om cirkelns radie är lika med $R$ . Volymen av en 2-dimensionell boll är således fastställd.

cirkel_area

Men hur räknar vi ut (hyper)volymen av en 4-dimensionell boll och hur definieras en sådan ens? Om vi ska fortsätta på samma sätt så måste vi definiera en $n$ -dimensionell boll på följande vis:

En $n$ -dimensionell boll med radie $R$ är ett område i $\mathbb{R}^n$ som innehåller alla punkter med koordinater $(x_1, x_2, \ldots, x_n)$ som uppfyller $x_1^2+x_2^2+\ldots+x_n^2\leq R^2$ .

Men hur ska vi ta reda på bollens volym? Genom att uttrycka den via de föregående volymerna! Volymen av bollen med radien $R$ i $n$ dimensioner, $V_n(R)$ , hänger nämligen ihop med volymen av bollen i $n-2$ dimensioner, $V_{n-2}(R)$ , på följande sätt:

$V_n(R)=\frac{2\pi R^2}{n}V_{n-2}(R)$

Detta bevisas genom att man ”delar upp” $n$ -bollen i $(n-2)$ -bollar (exempelvis den vanliga tredimensionella bollen kan ses som en massa vertikala streck) och sedan beräknar en dubbelintegral.

Formeln räcker, eftersom vi känner till volymerna för $n=1$ och $n=2$ , alltså kan vi konstruera formlerna för alla högre $n$ också.

$V_3(R)=\frac{2\pi R^2}{3}V_1(R) = \frac{2\pi R^2}{3}2R = \frac{4\pi R^3}{3}$ , som vi har sett tidigare.

Hyperbollen då?

$V_4(R)=\frac{2\pi R^2}{4}V_2(R) = \frac{2\pi R^2}{4}\pi R^2 = \frac{{\pi}^2 R^4}{2}$

Fler dimensioner? Från rekursionen deducerar vi en formel för udda dimensioner och en för jämna:

$V_n(R) = \frac{2^{\frac{n-1}{2}}\pi^{\frac{n-1}{2}}R^n}{1\cdot 3\cdot\ldots\cdot n}$ om $n$ är udda och

$V_n(R) = \frac{2^{\frac{n}{2}}\pi^{\frac{n}{2}}R^n}{2\cdot 4\cdot\ldots\cdot n}$ om $n$ är jämnt.

Vad beräknas volymen till då om radien antas vara 1? Vi får följande tabell:

$n$	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Volym, ca	2	3,14	4,19	4,93	5,26	5,17	4,72	4,06	3,30	2,55	1,88	1,34	0,91	0,60	0,38

Volymen går upp först men sedan verkar den gå det mot noll! Det intressanta är att trots att den 5-dimensionella bollen har störst volym av alla här, så är den egentligen inte så speciell. Om vi ändrar radien blir det någon annan dimension som ger en boll med störst volym (testa själv med hjälp av formeln, vid radie 1,29 är det istället den 9-dimensionella bollen som har störst volym.)

Det verkar lite skumt att volymerna går mot 0, men om man ser på formeln, så innehåller den exponentiella funktioner i täljaren, men i princip fakulteter i nämnaren. För stora tal dominerar fakulteterna alltid, alltså går kvoten mot 0 (och växer i början, för små $n$ , då fakulteterna inte än börjat ”ta fart”).

Ett annat sätt att tänka på det är att för att ekvationen $x_1^2+x_2^2+\ldots+x_n^2 = R^2$ ska vara uppfylld för stora $n$ måste många av talen $x_i$ vara nära 0. Exempelvis ligger punkten $(\frac{1}{\sqrt{n}},\frac{1}{\sqrt{n}}\ldots,\frac{1}{\sqrt{n}})$ på bollens yta och alla de koordinaterna närmar sig 0 när $n$ växer.

Texten ovan är baserad på följande artikel på engelska, som även innehåller beviset för rekursionsformeln. Stort tack!

Hur man multiplicerar matriser

Ju mer matteförklaringar är intuitiva, desto mer gillar jag dem. Matematik är svårare att förklara bättre på video än IRL på en tavla, men det finns undantag och det är då videoformen utnyttjas som mest.

Jag är nöjd över att ha hittat följande undantag: en video som berättar om matriser. Om du själv har svårt för att komma ihåg hur man multiplicerar matriser eller har en kompis som är det, rekommenderar jag att kolla på denna mästerverk i 4 minuter.

Pizzasats nummer 2

Matematik används inte bara när man ska skära upp pizza, utan också när man ska äta den. Möjligen har ni löst problemet nedan utan att ens tänka på matte.

När en pizzabit tas ut ur kartongen ser det ofta ut så här:
förväntning

Mot detta finns följande strategi:

Men varför fungerar det? Det hela beror på en sats som Gauss kom på.
gauss

Gauss sats har att göra med att alla ytor har så kallad krökning. Det är ett mått på hur mycket objekt kan böja sig utan att deras ”materiella” struktur förstörs (fler exempel på detta kommer senare).

Varje naturlig kurva har en specifik böjningsradie r i varje punkt. Storheten 1/r kallar vi då för krökningen i den punkten. Om kurvan är rak kring punkten, så säger vi att böjningsradien är oändligt stor och krökningen är lika med 0.

krökning

Samma definition gäller för ytor, men nu har punkten många olika värden på krökningen – en i varje riktning. Det maximala samt det minimala värdet av krökningen för en punkt kallas för huvudkrökningar.

kurvatur_yta

TIll exempel, på ett plan har alla punkter alltid krökning 0, medan på en sfär med radie R har alla punkter överallt krökningen 1/R. En cylinder med radien R kommer ha huvudkrökningarna lika med 1/R respektive 0.

kurvatur_cylinder

Om vi böjer lite på ett A4-papper, så kommer inte avstånden mellan punkterna på pappret att förändras. Sådana ändringar av ytor kallas isometrier.

papper

Om vi rullar ihop pappret, kommer vissa punkter ha ett kortare avstånd mellan sig än tidigare, eftersom nu finns det vägar som går genom kortsidorna som nu nuddar varandra.

papper_rulle

Gauss underbara sats (Theorema Egregium) säger att vid en lokal isometri kommer inte ytans Gaussiska krökning (produkten av huvudkrökningarna) att förändras.

Så länge pizzabiten ligger i kartongen är alla dess krökningar lika med 0.

pizzabit_kurvatur

Så fort pizzabiten tas ut, kommer den att böja sig. Då kommer ena huvudkrökningen att växa, medan den andra förblir 0.

pizza_sned_kurvatur

Men om kanterna viks upp kommer den sistnämnda huvudkrökningen sluta vara 0. Men enligt Gauss sats ska produkten av huvudkrökningarna förbli noll, det vill säga den andra huvukrökningen måste bli 0.

pizza_upp_kurvatur

Pizzabiten rätar ut sig och går bra att äta!

(Bilderna är tagna ur ryska internet, källa okänd. Tack konstnären!)

Theorema Egregium förklarar varför vi inte kan omforma ett papper till en boll utan att skrynkla ihop det. Inte heller kan en boll slätas ut till en sfär.

Det mest kända exemplet på detta är kartor. Jorden kan inte få en platt karta utan att avstånd förvrängs. Testa ett kartpussel för att övertyga dig om detta.

Trassel (tangles)

Aktiviteten trassel

Rekommenderas för: gymnasieet, universitetet (eller i förenklad form för högstadiet)

Materiel: två stora rep eller sladdar (gärna av olika färger), en ogenomskinlig plastpåse

Tid: 45 minuter

Antalet deltagare: 4 + publik

Aktiviteten ”trassel” kommer från matematikern och pusselkonstruktören Johan Conway och har genomförts i Sverige på bland annat Sonja Kovalevsky-dagarna. Den passar att genomföra på en matematiklektion om bråkräkning/gruppteori eller som en extra matematikaktivitet.

Man börjar med att fyra elever ställer sig som hörnen på en kvadrat inför resten av klassen. Var och en av dem tar tag i var sin ände av ett rep så att repen hänger parallella med hur publiken sitter. Under experimentet får de aldrig släppa sin ände.

Så här ser det ut uppifrån (Positionerna närmast klassen är D och C):

trassel start

Nu kommer de fyra personerna utföra en slags dans och trassla till repen samtidigt. Varje trassel (tangle) repen bildar kommer att ha ett motsvarande tal. Från början, när repen är parallella mot varandra och mot klassen, motsvarar det talet 0.

Det första tillåtna danssteget är att vrida om repen runt varandra. Och inte på vilket sätt som helst, utan det måste göras av personerna som står på positionerna B och C. Dessa två personer byter plats med varandra och B är den som lyfter sin repände, som C går under för att komma till sin nya position.

vrida om

Att vrida om trasslet på det här sättet kommer att öka talet med 1. Så en omvridning ger ett trassel med värdet 1, medan en till omvridning ger talet 2 osv.

Det andra tillåtna danssteget är att rotera medurs. Person A går till position B, person B går till position C och så vidare.

Att rotera trasslet kommer också att förändra talet. Men hur? Om elevera har hållit på med funktioner och algebra tidigare kan man låta dem att lista ur svaret. Annars kan man helt enkelt säga att talet x omvandlas till talet -1/x vid en sådan rotation. Notera t.ex. att två rotationer i rad inte gör någon skillnad på trasslet, vilket är klart för trassel som består av några omvridningar:

n -> -1/n -> -(1/(-1/n)) = n

rotera

När alla har förstått reglerna kan man be eleverna att uföra några danssteg (börja med att först
vrida om), samtidigt som man räknar på talet som ska motsvara trasslet. Om man från början gör dansstegen: vrida om, vrida om, rotera, vrida om, vrida om, vrida om, rotera, vrida om så kommer man till talet:

0 -> 1 -> 2 -> -1/2 -> 1/2 -> 3/2 -> 5/2 -> -2/5 -> 3/5

Hur ska man lösa upp detta trassel om man bara tillåts att göra dansstegen ovan? Publiken får lösa denna uppgift genom att försöka räkna ut hur man ska göra med bråket 3/5 för att det ska bli 0, om man bara tillåts addera 1 och ta den negativa inversen. Man kan ju inte göra dansstegen ”baklänges”, eftersom steget ”att vrida runt åt andra hållet” inte finns.

När någon har kommit på dansstegsföljden kan man testa dansen och se att knuten verkligen löses upp.

Det här kan man göra med andra tal. Ju svårare trasslet är, desto roligare blir det att se det lösas upp. När repen är tilltrasslade, kan man knyta några plastpåsar runt dem, så att trasslet inte syns och sedan utföra dansstegen som eventuellt ska lösa upp trasslet. När talet på tavlan är 0 kan man knyta upp påsarna och se att allt blir som i början, bara man drar i repen!

Fler frågor att diskutera på avancerad nivå:

– Vad händer om man roterar först? Vad är talet -1/0 och vad har det för egenskaper? Ska trasslet -1/0 förändras om man vrider om det?

– Hitta inversen till att vrida om. Det vill säga, om man startar från ett trassel och sedan vrider om en gång, vad för danssteg skall man göra för att komma tillbaka till starttrasslet?

Fler frågor för att grupper:

– Om man börjar från 0, hur kommer man till ett specifikt trassel, t.ex. -3?

– Hut kommer man snabbast ner till 0 från ett specifikt trassel? Här kan eleverna tävla om vem som kan hitta på kortaste dansstegsekvensen när trasslet är ett relativt avancerat bråktal.

Mer om aktiviteten kan du läsa i Conways text (tangles börjar på sida 10) conway.pdf, samt Tom Davis text med utförlig diskussion och beskrivning av aktiviteten. tangle.pdf.

Tack till Johan Björklund för tipset!

Bas 10

En alien med 4 fingrar och en människa möter varandra:

Vad är en bas?

De flesta förstår räkning med olika baser utan att behöva lära sig någon formell definition. Vi räknar i bas 10 och det finns ental, tiotal, hundratal och så vidare. Vi har 10 siffror: 0,1,2,3,4,5,6,7,8,9 och varje (naturligt) tal bestäms entydigt av att några siffror skrivs i en viss ordning.

Men vad händer om vi har brist på siffror? Datorerna har bara siffrorna 0 och 1 till exempel. Eftersom det är två siffror säger vi att datorernas tal är skrivna i bas två. De första sju talen skulle då vara: 1,10,11,100,101,110,111. Vad långa talen blir! Så kan det gå när det finns så få siffror. Har vi brist på siffror, måste vi använda fler potisioner.

Vad händer om vi hittar på egna siffror? Låtsas som att vi har sexton siffror: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F. Då kan vi räkna i bas sexton:
Exmpelvis kommer talet 9999 precis före talet A000. Det största sexsiffriga talet är talet FFFFFF och så brukar man beteckna färgen ”vit” hexadecimalt (det vill säga i bas sexton)!

Varför skulle varje bas vara bas 10?

Hur kommer det sig att alienen med fyra fingrar räknade i bas 10? Det är för att han själv tycker att han har 10 fingrar! De första fyra talen skriva i hans bas är nämligen 1,2,3,10 (han har bara fyra siffror).

Detta verkar hända med varje bas. Om vi räknar i bas n, så har vi n siffror (varav t.ex. 0 är den första), vilket betyder att de första n-1 positiva heltalen kan betecknas med bara en siffra. Men för ett tal till (och det blir talet n) behöver vi två siffror! Det minsta tvåsiffriga talet betecknas just 10 (om vi valde just 0 och 1 att beteckna de minsta siffrorna).

Bas ett?

Inga konstigheter verkar ske när vi räknar med bas två eller någon annan större bas. Baserna följer samma räkneregler som vanligt, vi behöver bara hålla reda på vilka siffror som finns tillgängliga.

Men hur skulle man kunna räkna med bas ett? Om det bara är en siffra tillåten, hur ska vi då kunna skriva 10, som ska beteckna vår bas med hjälp av just vår bas?

Det går inte, vi kan bara skriva en symbol, så alla talen måste skrivas olika långa för att vi ska kunna skilja på dem. Om vår symbol är a, så ser våra fem första positiva heltal ut så här: a, aa, aaa, aaaa, aaaaa.
Men ska vi välja en siffra istället för a och i så fall vilken siffra?

Större baser har ju den egenskapen att talen är lätta att ”räkna om” till vårt vanliga bas tio.
T.ex. så är 1011 i bas två lika med

1*8+0*4+1*2+1*1 = 11

i bas tio, och 30A i bas sexton är lika med

3*256+0*16+10*1 = 778

i bas 10.

Hur blir det då med talet aaa i bas 1?

a*1+a*1+a*1 = 3

Då är 3a = 3. Alltså är a=1. Och talet ett i bas ett måste skrivas just 1.

Notera att om alla tal i bas 1 består av 1:or så är det omöjligt att skriva talet 0. Positionssystemet fungerar inte heller som det brukar, eftersom alla positioner står för exakt lika mycket: 1. Tal adderas då genom att skrivas ihop:

111 + 1111 = 1111111.

Om vi vill ha ett talsystem som ska kallas för bas ett och behålla så mycket egenskaper för en bas som möjligt, så har vi hittat det. Vi kan dock omöjligen hitta något som behåller alla egenskaper och kallas för bas 10 i sin egen beteckning.

Kvaternioner

Enligt en broinskription (se bilden nedan) upptäcktes kvaternionerna för exakt 169 år sedan, då William Hamilton tog en promenad i Dublin med sin fru. Hamilton kände till de komplexa talen (till exempel talet $i$ som uppfyller likheten $i\cdot i = -1$ ), men han ville utvidga dem ytterligare till en större talmängd, som fortfarande skulle uppfylla de viktigaste talegenskaperna.

Han kom då på mängden kvaternioner (betecknas $\mathbb{H}$ ), som förutom vanliga tal och $i$ även innehåller talen $j$ och $k$ , som uppfyller följande:

( $i\cdot i = -1$ , denna egenskap är kvar från de komplexa talen)
$j\cdot j = -1$
$k\cdot k = -1$

$i\cdot j = k$
$j\cdot k = i$
$k\cdot i = j$

Det spelar förstås ingen roll vilka bokstäver man väljer att beteckna de här nya talen med, det viktiga är deras egenskaper och samverkan med varandra.

Notera att multiplikationen talen emellan är lite märklig. Desto märkligare är att $i\cdot j$ inte blir samma sak som $j\cdot i$ , det vill säga Hamilton lyckades inte behålla multiplikationens kommutativitet. Man adderar och subtraherar dock kvaternioner precis på samma sätt som man skulle göra med de komplexa talen. Man kan addera de olika bokstäverna med varandra och exempelvis gäller:
$(1+2i+j) + (2+i-j+k) = 3+3i+k$

Hur kan vi lista ut vad $j\cdot i$ bör bli lika med? Tänk på att vi inte kan byta plats på faktorerna, men vi kan multiplicera med något nytt ”från vänster” eller ”från höger”. Säg att vi multiplicerar med $i$ från höger:

$(j\cdot i)\cdot i = j\cdot (i\cdot i) = j\cdot (-1)=-j$

Så att vårt svar multiplicerat med $i$ från höger ska också vara lika med $-j$ . Vad kan det vara för tal?
Om du inte kan komma på det, tänk på vilket tal multiplicerat med $i$ från höger blir lika med $j$ istället och modifiera svaret efter det.

Man kan göra en liten grundmultiplikationstabell för de komplexa talen:

Kan du lista ut vad som står istället för frågtecknen i multiplikationstabellen för kvaternionerna?

En övning i kvaternioner: Vad blir $(1+i+j)(2-j+k)$ ?

Det går att dividera kvaternioner med varandra, resultatet av en division blir alltid ett kvaterniontal (så länge man inte dividerar med 0).

En till övning: Vad blir $1/(i+j)$ för kvaterniontal?