Mattegåta
Ett biljardbord har en långsida som är dubbelt så lång som kortsidan. I varje hörn finns det ett hål, samt två hål till finns på varje långsidas mitt.
Vilket är det minsta antalet bollar som man kan placerat ut på bordet så att varje hål befinner sig på samma linje som ett visst par av bollar? (Bordet är rektangulärt, hål och bollar antas vara lika stora som punkter.)
Diskussion
Eftersom det frågas efter det minsta antalet i uppgiften är det underförstått att resultat skall bevisas. Det vill säga det måste finnas ett exempel med x bollar (om x är svaret), samt bevis för att det inte går med färre än x bollar.
Ett sätt att jobba på är att börja underifrån (till exempel med 1 eller 2 bollar) och för varje antal antingen visa att det inte går eller att det går. Fallen är oftast svårare närmast svaret. Lite som i fyrfärgsproblemet!
Fyrfärgsteoremet
Sats. För en platt ”karta” räcker det alltid med fyra färger för att måla ”länderna” på kartan så att inga två länder med gemensam gräns har samma färg (gränser utgörs av raka eller krokiga linjesegment).
Det var länge känt att det räckte med fem färger och att det finns kartor som inte går att färga med tre färger. Men fallet fyra tog lång tid tills den äntligen bevisades med hjälp av datorberäkningar.
Lösning (av Erik Svensson)
Till att börja med kan vi uppenbart utesluta att det går med bara en boll (och förstås även med noll bollar).
Det finns ej heller någon lösning för två bollar, ty vi vet att två bollar (punkter) entydigt bestämmer en linje, så om samtliga hål ska ligga i linje med två bollar, då måste alla hålen ligga på samma linje. Men hålen på biljardbordet ligger inte på en linje.
Det är inte heller möjligt med tre bollar, vilket vi ser om vi försöker konstruera en. Om vi har tre bollar, då finns det två möjligheter: Att de ligger på en linje eller att de inte gör det.
Ifall de ligger på en linje, då får vi en motsägelse med samma resonemang som för två bollar, och ifall de inte ligger på en linje så bildar de en triangel. I så fall utgör varje linje med två bollar en sida i denna triangel, och bollarna är hörnen.
Vi börjar med att konstatera att ingen sida i denna triangel kan täcka tre hål, ty de enda linjerna på bordet som täcker tre hål är långsidorna. Ens om vi antar att frågeformuleringen tillåter bollar längs med sidorna innebär detta att två bollar måste ligga på en av långsidorna, vilket innebär att den tredje bollen måste ge upphov till två linjer som täcker samtliga tre resterande hål, vilket medför att någon av dessa två linjer måste täcka två hål på den andra långsidan och ändå korsa den första långsidan, vilket är omöjligt.
Att täcka fyra eller fler hål med en linje är förstås också omöjligt som biljardbordet är uppbyggt.
En linje kan ej heller passera genom bara ett hål, eftersom detta lämnar fem hål att täckas med de resterande två linjerna, och alltså måste någon av dessa linjer täcka minst tre hål, vilket motsäger det vi just kom fram till. Även en linje som inte täcker några hål kan vi utesluta, eftersom denna linje i så fall kan tas bort och därmed ge en lösning för två hål, vilket vi visat inte existerar.
Således måste vi ha tre linjer som täcker exakt två hål, och de måste täcka två bollar vardera. Eftersom varje boll är ett hörn i den triangel som bildas ligger varje boll på två sådana linjer.
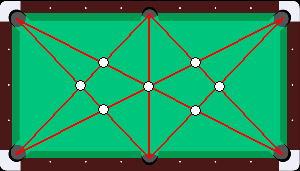
På bilden ser vi alla möjliga linjer som täcker två hål, samt alla skärningspunkter mellan dem. Dessa punkter är de enda kandidaterna till var en boll kan ligga. Vi ser emellertid att det inte finns någon triangel av sådana punkter (med de utmarkerade linjerna som sidor), och den minsta slutna figur vi kan bilda är en fyrhörning. Alltså finns det ingen lösning för tre bollar, men det finns en för fyra, till exempel genom att välja fyra punkter som bildar en fyrhörning i bilden och lägga bollarna där.