Hungrig student
[kkratings]
Pelle har en stekpanna som det får plats två hamburgare i samtidigt. Han vill steka varje hamburgare på varje sida i 2 minuter. Pelle är hungrig och vill steka tre hamburgare så fort som möjligt. Vilket är den kortaste tiden det kan ta?
12 reaktioner till “Hungrig student”
Lämna ett svar
Denna webbplats använder Akismet för att minska skräppost. Lär dig hur din kommentardata bearbetas.
6 minuter ;)
Håller med Martin.
Generalisering: n hamburgare, m stektid och k stekpannor. Någon?
Och det får plats r hamburgare åt gången? :)
Det känns lite som problemet med familjen som ska ta sig över bron, dock mycket svårare. Har du löst någon specifik generalisering än Toomas?
Med s sidor var?
Nej, jag har haft annat för mig. Jag ska titta närmare på det snart.
Några första tankar:
Antag att vi har k stekpannor och n hamburgare, vilka har 2 sidor var (det är ju ingen hamburgare annars). Varje sida har en stektid på m tidsenheter. På varje stekpanna får det plats r hamburgare åt gången.
Det totala antalet sidor som vi vill steka är 2n. Den totala stektiden alla sidor räknade separat är 2nm, vilket också utgör ett maximivärde, förutsatt att vi steker åtminstone en sida åt gången kontinuerligt.
Det totala antalet platser på stekpannorna är rk. Vi kan dock endast steka n sidor åt gången, ty den andra delen av hamburgaren då är onåbar.
Om rk≥n, har vi minimerat tidsåtgången. Det går då att steka allt i två omgångar, helt enkelt genom att vända sida, vilket ger en minimal stektid på 2m. Oavsett värdet på variablerna, kommer tiden t vara sådana att 2m≤t≤2nm. Då vi prövar några värden, får vi ingen motsägelse, så det finns indicium på att resonemanget stämmer.
Om rk<n, kan vi inte ha alla hamburgare på samtidigt, likt detta exempel. Vi vill dock fortfarande fylla alla rk platser till största möjligaste mån. Fyll då i omgång 1 alla. Antag att h hamburgare blev över. Då har vi fortfarande kvar att steka 2n-rk+2h sidor.
Härifrån är det konstruktivt att dela upp i alla kombinationer av udda/jämn antal platser rk och udda/jämn antal hamburgare n. Nu måste jag dock övergå till annat.
Jepp, du har bevisat att 2m är minst och 2nm är störst.
Ja, det är just fallet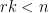
som utgör det intressanta i problemet. I vilka fall går det att tjäna på att vara smart? Hur gör man?
Problemet kan dessutom ställas på olika sätt: man kan tillåta stekning av mindre än en sida åt gången (vilket gör problemet lättare, eftersom tiden kan då uttnyttjas maximalt varje gång det går). Alltså borde vi titta på när endast en sida åt gången är tillåten. Det vill säga har vi diskreta tidssteg.
Varje enhetssteg ger rk stekta ytor som bäst. Vi kan tänka att det egentligen är 2n ytor som ska stekas en gång var, men högst n kan stekas åt gången (så är det i vilket fall om kr < n). Det verkar som att problemet i detta fall också blir trivialt: stek så många halvor som möjligt i varje tidssteg, då uttnyttjas tiden maximalt. Prioritera ostekta hamburgare före halvstekta. Nu var det inget strikt bevis, men jag tror att det är lösningen. En mer innehållsrik fråga får vi om hamburgarna (vi kanske bör döpa dem till bullar eller nåt) har 3 sidor eller fler.
hmmm, om studenten vill har varje hamburgare stekt två minuter på varje sida så tar en hamburgare minst fyra minuter att färdigställa och svaret kan inte vara tre minuter ens för en ensam hamburgare :-)
Aah .. Tack Lotta, jag redigerar lösningen :)
vet ej!
Jag tror jag bevisat en ganska så formell lösning för det generella fallet med n burgare, k stekplatser, s sidor och m minuters stektid, där vi måste steka varje sida fullt ut (annars blir det såklart mycket lättare).
Antag n hamburgare, k möjliga stekplatser (antal stekpannor*plats per panna), och s sidor, och varje sida kräver m minuters stektid.
Det är alltid optimalt att påbörja stekningar enl. en definerad ordning så fort det finns plats, och vi kan därmed anta att alla stek-skiften sker vid tidpunkterna im där i är ett naturligt tal. Detta gör att vi kan anta m = 1.
Detta kan formuleras: Vi har n grupper av s jobb som alla tar lika lång tid att utföra. Ett jobb kan processeras av k olika arbetare, och ur en grupp får högst ett jobb processeras åt gången. Hur schemalägger vi jobben optimalt?
Det totala antalet jobb som måste utföras är sn. Numrera alla grupper av jobb 1, 2, …, n.
Betrakta jobb-schemat 1, 2, 3, 4, …, n, 1, 2, 3, … n, osv s gånger.
Är k >= n, kan vi helt enkelt utför alla arbeten direkt, och vi upprepar det s gånger. Det tar då s tidssteg. Därmed kan vi anta att k < n.
Det är ju som sagt alltid optimalt att vid ett tidssteg då de k nuvarande arbetena är klara utföra de nästa k arbetena i kön om möjligt. Därmed kommer vi minst behöva ceil(sn/k) tidssteg för att slutföra hela kön med sn jobb. Men det föreslagna schemat kommer vi vid varje tidpunkt kunna utföra antingen k, eller alla de resterande jobben. Detta för att k < n, och varje jobb ur samma grupp är exakt n steg ifrån varandra. Alltså kommer det schemat också kräva precis ceil(sn/k) tidssteg.
Vi vet alltså att ceil(sn/k) <= t <= ceil(sn/k), där t är den optimala tiden. Alltså behöver vi exakt m * ceil(sn/k) tidssteg för att steka alla hamburgare.
Ex. har vi i det ursprungliga problement n = 3, s = 2, k = 2, m = 2;
Då behöver vi 2*ceil(2*3 / 2) = 2*3 = 6 minuter för att steka alla hamburgare.
Jag håller med om att detta löser det allmänna fallet med diskreta tidssteg. Tack, JS!