Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.
Här kan du se vad vi tidigare har gått igenom.
Grafer
Jag försökte att introducera grafer på den allra första lektionen men begreppen tog sig inte. Det var inte naturligt för fem- och sexåringarna att representera människor med prickar och syskonsrelationer med pilar. Eller så passade inte temat till att vara först av alla helt enkelt.
Därför tänkte jag prova igen att bekanta barnen med grafer, denna gång med en mycket mjukare introduktion. Därför handlar egentligen inte så stor del av lektionen om grafer.
Barn ska kunna differensiera enkla linjära former
Titelt är ett skämt och betyder ungefär att barn ska kunna skilja på cirklar, trianglar och kvadrater.
Dagens lek går ut på att bygga ett land som består av öar. Öarna har alla olika färg och form: cirkel, rektangel, ring, femhörning etc. Barnen ska kunna nämna alla formerna. Vi placerar öarna på ett stort blått papper som symboliserar havet.
Broar
För att öarna ska bilda ett rike, måste det finnas sätt att ta sig emellan dem. Barnen får en bro i taget (en platt avlång rektangel), som kan förbinda två öar med varandra. Vilket är det minsta antalet broar som behövs för att man ska kunna promenera runt hela landet?
När vi har byggt det minsta antalet broar som krävs för att landet skall vara sammanhängande (vilket är 1 mindre än antalet öar). Hur många broar till kan vi bygga, om inte två broar får korsa varandra (broarna får vara böjda)? På den sista frågan vet inte jag det exakta svaret. Tillsammans med barnen ska vi i alla fall hitta ett lokalt maximum, det vill säga en situation där ingen ny bro kan sättas in, hur den än slingrar sig, på grund av korsandet av andra broar.
Köningsbergs broar
Man bestämde sig för att måla om alla broarna i landet till en ny färg. Går det att köra med målarbilen exakt en gång på varje bro? Det vill säga aldrig köra på en och samma bro två gånger och inte heller utelämna någon bro.
Barnen får göra minst ett försök var. Det tar ett tag innan man hittar den rätta vägen, om den nu existerar!
Detta är samma problem som Köningsbergs broar. Bara formulerat lite annorlunda.

Rita utan att lyfta pennan
För de äldre barnen passar uppgiften: rita figuren utan att lyfta pennan från pappret medan du ritar.
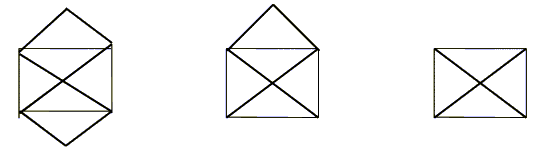
Auktion
Varje barn får ett och samma antal pappersmynt. De får i hemlighet bjuda ett visst antal mynt på varje ö. Den som bjuder flest mynt, får bli öns president (om det är lika, bjuder man om). Mynten man har kvar, kan man spendera på byggblock, som man får bygga presidentpalatset av på sin ö.
Detta lär barnen hur en bjudning kan fungera. Också lär de sig att snabbare jämföra antal och avgöra vem som bjöd flest mynt.
Karta
Det är dags att rita landets karta! Rita av landet på ditt eget papper. Du kan börja med ön där du är president och rita resten därifrån.
Samtidigt som barnen ritar jag en ”karta” där öar bara är prickar och broar är streck. Sedan får barnen se kartan. Kan alla peka på sin egen prick?
Flaggor
Landets färger är blått (havets färg), gult (solens färg) och rött (broarnas färg). Vi vill att landet inte bara ska ha en flagga, utan alla möjliga randiga flaggor som består utav 1, 2 eller 3 ränder!

Barnen får tillsammans måla alla flaggorna och kontrollera att de ha tagit alla kombinationer. Eventuellt kommer de på att man kan ha ränderna på det andra hållet (som i den rumänska flaggan och inte den ryska). Om ränderna är som på bilden ovan, finns det 15 olika flaggor man kan göra.
Set
Om det blir tid över, spelar vi set med de äldre barnen. På spelet står det att lägsta åldern är 6, men jag tror att det är meningsfullt att köra spelet först vid 7.

Hejhej! :) Jag tycker det här verkar som en jätterolig lektion! :) Du får gärna berätta hur det går sen! :)
Hur lång tid tar varje lektion och var hålls de? Stockholm?
Hej! Det gick faktiskt väldigt bra, och lektionen passade i princip i samma förmat för alla från 5 till 10 år. Vi hann inte göra flaggor och spela set, men alla barnen fick chansen att försöka gå på alla broarna exakt en gång.
Alla grupper utom den sista byggde ett land, där det inte gick att gå en sådan rutt, men några av barnen lyckades ändå med en maximalt lång rutt (en bro blev över), och i gruppen där rutten var möjlig hittade de en sådan faktiskt.
Våra lektioner är 30-45 min långa (30 för femåringarna), varav 9 minuter brukar de kolla på en liten mattefilm. Vi håller hus på Cybergymnasiet i Stockholm, vid Odenplan.
Johans kommentar:
”Jag tror att med v öar så kan du använda maximalt 3(v-2) broar när v>2. Beviset kan vara som följer. Tänk dig att du ritar noderna på en sfär istället för på ett plan (det gör ingen skillnad eftersom vi kan strunta i att dra saker över nordpolen då den bara är en punkt). Antag att vi har en optimal konstruktion. Då kan inget område innehålla en polygon med fler än tre hörn, ty om vi har fler än tre hörn så kan vi koppla två som inte ligger bredvid varandra med en bro tvärsöver polygonen (om de redan är kopplade så kan inte deras grannar vara kopplade, vilket syns lätt med en bild). Jag kallar en sådan konstruktion för triangulär (att jag vill vara på sfären är för att kunna säga att området mot oändligheten är triangulär på ett vettigt sätt). En optimal konfiguration måste då vara triangulär.
(Jag tror att det borde gå att göra ett argument där man utgår från att en optimal konstruktion i steg k+1 kan fås från en optimal konstruktion i steg k, isåfall så måste den nya punkten läggas till i en triangel och alltså kan den bara ge upphov till 3 nya broar. Detta skulle ge att bro antalet ökar med 3 per steg. Om man inte lyckas med det argumentet så kan man göra som nedan).
Tag en triangulär konfiguration med v noder, k broar och f ”trianglar”. Då varje bro separerar två trianglar och varje triangel skapas av tre broar så har vi att 2k/3=f. Då Eulerkaraktäristiken på en (2-dim) sfär är 2 så har vi att v-k+f=2, detta ger att v-2=k/3, och vi får 3(v-2)=k.
Jag håller med Lisa om att det verkar vara en kul lektion :)
Har du funderat på att göra något inspirerat av fyrfärgsproblemet? Att färglägga saker kan ju vara kul (och mha fyrfärgsproblemet så finns det ju alltid en lösning, så då kan man ju snabbt generera kartor som folk får rita på).”
Mitt svar på Johans kommentar:
”Tack för beviset och tack för fyrfärgstipset också. Jag funderade på att ha någon lektion om geografi/kartor (innan jag kom på denna lektion i och för sig), så det passar ju perfekt som utgångspunkt.”
På tal om rolig matte, har du tittat i Kristin Dahls böcker ”Matte med mening” och ”Kvadrater, hieroglyfer och smarta kort”? När jag var nio-tio år var jag helt galen i dem. :) De innehåller allt möjligt roligt: pythagoras sats, kvadrattal, kanske t o m chiffer och så förstås möbius band. Allt är dessutom förklarat på en nivå som är lätt att förstå. :) ”Matte med mening” är dessutom rolig för att den är illustrerad av Sven Nordqvist, författaren av Pettson och Findus, så boken innehåller en massa roliga mucklor. Tyvärr är boken på svenska. :P Men jag tänkte att den kan innehålla en del inspiration till roliga aktiviteter. :)
En annan superhäftig barnbok är ”Sifferdjävulen : en bok att stoppa under huvudkudden, för alla som är rädda för matematik”. :) Den är dock mer en läsebok än en bok som man kan bläddra i. Men den är spännande! :D Den handlar om en pojke som är rädd för matematik, och en natt kommer en sifferdjävul in i hans drömmar och tvingar honom att lära sig rolig matematik. Den behandlar bl a triangeltal, kvadrattal, fakulteter, 1+2+3+..+99+100 och en massa annat som jag inte längre fattar hur det kan vara kul, men som jag tyckte var häftigt då. :) Dessutom berättar de allt på ett sådant sätt att man inte kan låta bli att uppslukas av boken och att skratta.
Vilka bra tips, Lisa! Och det gör inget att böckerna är på svenska, jag har ju några svenska elever också.
Ska absolut köpa dem :)