Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.
Här kan du se vad vi tidigare har gått igenom.
Mönster
Väldigt mycket i matematiken handlar om att se mönster. Jag skulle vilja påstå att det mesta inom grundskolans matematik går ut på att lära sig se ett slags mönster i uppgifter för att kunna tillämpa metoder.
Mönster som 3 + 7 = 10 hjälper en att lösa uppgifter som 14 + 3 + 7 = 24.
Och ifall man är bra på att extrapolera mönster, kan man komma på formler alldeles själv!
Upprepningar
Gjorde ni också girlanger utav gubbar till julgranen? Pojkarna nedan är ganska enkla att göra, men hur gör man för att klippa ut en girlang med varannan kille, varannan tjej?

Se mönstret och fortsätt
Ett bevis på att man ser mönstret i bilden är att man kan fortsätta det. Och tvärtom, om man försöker fortsätta mönstret ser man kanske när det blir fel och när det blir rätt.
Om man väver några remsor kan man se ett mönster i hur de synliga bitarna är färgade. Vilka färger finns underst respektive överst där bokstäver A och E står?

Föreställ dig mönstret
Ju mer matematik man läser, desto mer behöver man tänka abstrakt. Det innebär ofta att föreställa sig saker som inte finns framför en. Ibland föreställer matematiker sig saker som ingen har sett (som till exempel fyrdimensionella objekt)!
Förmågan att föreställa sig fysiska objekt och förhållandet dem emellan kallas för spatialförmåga. Den är väldigt viktig för pilot- och militäryrket, och så förstås matematikerna. För att träna den skall de lite äldre barnen lösa följande pussel:

Utan att kvadratbitar får klippas ut och arrangeras om, skall man bestämma vilken på som ska vara på vilken plats. Det betyder att bitarna måste arrangeras om i huvudet. Du kan prova själv genom att fylla i en en följande tabell med motsvarande tal.

Föreställ dig något som inte syns
En klassisk uppgift är att bestämma hur många kuber ingår i konstruktionerna, utan att alla kuberna syns.
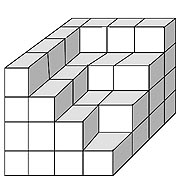
Efter att alla barnen har skrivit ner förlaget, bygger vi upp sktrukturen och räknar hur många kuber det faktiskt behövdes.
Perspektiv
De äldre barnen får träna spatialförmågan på ett tredimensionellt sätt. De får se en bild på kubens alla sidor (i utvikt format), och sedan avgöra hur tre av kubens sidor ska se ut när man kollar på den från olika vinklar.
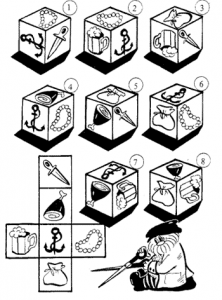
Tillverka en kub
Vi ska kombinera några av de ovastående övningarna och tillverka en kub själva. För det första skall barnen lista ut vilka av kvadraternas sidor skall tejpas ihop med vilka. Sedan får alla ett papper med ett mönster.
Uppgiften är nu att klippa upp mönstret i 6 likadana kvadrater. Varje kvadrat klistras sedan på en av sidorna på någons kub.
Det svåra är att klippa exakt utan att mäta. Tricket är att kolla på kanten, till exempel den vänstra. Då ska man klippa i bilden precis där den vänstra kanten av högra halvan är likadan som vänstra kanten av vänstra halvan. Skriv ut och försök själv!


Hej.
Är matematik/fysiklärare på gymnasie/högstadie och vi diskuterar hur man ska få ungdomar att börja tävla i matematik igen, som vi gjorde när vi gick i skolan.
Men man kanske kan angripa problemet från ett annat håll.
Matematik är för många kopplat till spatial förmåga.
Så vi tror att ett effektivt sätt att öka ungdomars matematiska förmåga är att få dem att spela 3D Tetris som tex detta.
https://blockOut.nu
Arrangera tävlingar/turneringar med priser i klass/skola/stad/län och sedan landsfinal och se om det kan påverkar resultaten.
Jag utmanar själv mina elever i detta och tror det är ett mycket bra sätt att få studenter att träna sin spatiala förmåga samt då öka deras matematiska förmåga.
Eller vem ska man kontakta för att få detta testat?
Mvh
M.Sc. Magnus Ivarsson