En konvex fyrhörning ABCD har kända sidlängder: AB = 5, BC = 10, CD = 14, DA = 11. Fyrhörningens diagonaler skär varandra med en viss vinkel. Hur stor är den vinkeln?
Eftersom fyrhörningen är konvex skär diagonalerna AC och BD varandra inuti fyrhörningen. Kalla skärningspunkten för P. Från skärningspunkten ut till hörnen går fyra sträckor: PA, PB, PC och PD. Låt de ha längderna a,b,c respektive d.
Då kan vi skriva cosinussatsen för alla fyra trianglarna som diagonalerna delar upp fyhörningen i:
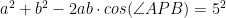



Men notera att  , men också
, men också  . Så första och tredje vänsterledet tillsammans är alltså lika med andra och fjärde vänsterledet tillsammans:
. Så första och tredje vänsterledet tillsammans är alltså lika med andra och fjärde vänsterledet tillsammans:


När alla kvadraterna försvinner får vi:
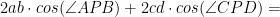
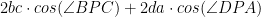
Men notera att 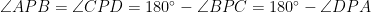
Då gäller att 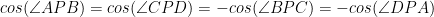
I så fall kan vi förenkla vår tidigare likhet:


Och ytterligare:

Men a,b,c,d är alla positiva, eftersom de är längder, således måste  .
.
Det finns bara en vinkel som kan uppfylla detta, nämligen 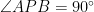 .
.
Kan man hitta någon fyrhörning med sidorna 5, 10, 11 och 14 som har större area
än fyrhörningen i detta exempel?
I det här exemplet pratar vi inte om en fyrhörning, utan en hel grupp med fyrhörningar som har sidlängderna i just ordningen 5, 10, 14, 11.
Enligt wikipedia så har den cykliska fyrhörningen störst area bland alla med samma längder på sidorna. Men jag kommer inte på hur man räknar ut arean i de tre olika fallen vi har med de givna fyra sidlängderna.
Du kan använda Brahmaguptras formel för en cyklisk fyrhörning (en generalisering av Herons formel), se http://en.wikipedia.org/wiki/Brahmagupta's_formula. Den ger arean som en funktion av sidorna (och pga symmetri hos uttrycket så gör det detsamma i vilken ordning sidorna kommer). Detta gör att vi inte kan få någon ”större” fyrhörning.
Det kan också ses geometriskt rätt lätt. Tänk dig att du har fyrhörningen ABCD inskriven i en cirkel. Vi vill byta plats på AB och BC. Drag linjen AC och dra sedan linjen som går igenom origo som är ortogonal mot AC. Spegla B i den linjen. Då hamnar B på B’. B’ ligger fortfarande på cirkeln då den är invariant under speglingar m.a.p. origolinjer och A skickas på A samt C skickas på C. Alltså så skickas triangel ABC på AB’C som har samma area. Då har fyrhörningen AB’CD samma area som ABCD (då den består av två trianglar, den ena gjorde vi inget med och den andra behöll arean). |AB|=|B’C|, |BC|=|AB’| så vår nya fyrhörning har bara bytt plats på två sidlängder. Atta kunna byta plats på två nästrående sidor genererar permutationsgruppen, och alltså är area hos cykliska fyrhörningar invariant under permutationer.
Oj, jag menar att A skickas på C samt C skickas på A av speglingen…
Hej Johan B.
Vilken är den minsta area fyrhörningen kan ha om den tillåts vara konkav?
Ja, såklart, Johan! Tack! I detta exempel blev arean till och med ett heltal, 90.
Sture! Det verkar som att minsta arean är 20 (experimenterade här: http://keisan.casio.com/exec/system/1322718508), men jag känner inte till någon formel för beräkning av den.
Hej Val
Jag fick minsta arean till 12*sqrt(10) Den konkava fyrhörningen övergår i en triangel
med sidorna 9,10,11. Jag kan skicka mina lösningar till dem som önskar sådana
sture.sjostedt@spray.se
Hej Val!
Jag upptäckte att 6,10,14 ger en mindre triangel med arean 15sqrt(3). Ganska exakt 26
Hej Val!
Förstoras en Egyptisk triangel till (15,20,25) kan den läggas mot (7,24,25).Den unionen har arean 234. Om fyrhörningen har två räta vinklar klarar man sig med Herons formel och Pythagoras sats.En cirkel med radien 65 ger i första kvadranten (16,63,65),(25,60,65),(33,56) och(39,52,65). Ritar man en cirkel med diametern och tillverkar stavar som kan sammanfogas till fyrhörningar med leder i hörnen kan man göra många intressanta undersökningar då fyrhörningen genomgår följande utvecklingsstadier :1)konvex fyhörning(maximal area) 2)triangel 3)konkav fyrhörning 4)triangel (minimal area ??)Man måste vända på den ena triangeln och göra om undersökningen. Sidornas inbördes ordning påverkar arean då man minimerar arean.
Hej Sture!
Ja, det är inte alls säkert att den generaliserade icke-konvexa fyrhörningen (triangeln) har minimal area, vilket är intressant. Samma sak med sidornas inbördes ordning, jag är inte heller säker på att det påverkar den minimala arean.
Hej Val!
Du har nog rätt. Man får göra en modell och pröva för några fall.