Kryssa grannrutor

(a) Ja, Esteban kommer lyckas oavsett hur Chiyen börjar. Låt oss tänka att rektangeln har 8 rader och 9 kolumner. Från rutan där Chiyen början kan han kryssa i en hel rad genom att kryssa en ruta åt vänster i tager och sen en ruta åt höger i taget. När raden är klar, kan Esteban kryssa i hela första, tredje, femte, sjunde samt nionde kolumnen, genom att som förut ta en ruta i taget (denna gången uppåt, sedan neråt).
Nu kan rutorna i andra, fjärde, sjätte och åttonde kolumnen kryssas en i taget också, utgående från startraden, eftersom de kommer ha 3 ikryssade grannrutor om man börjar från startraden.

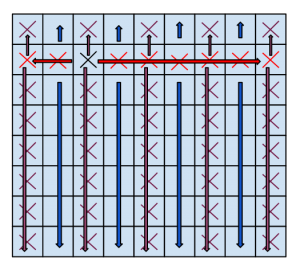
På bilden startar Chyien med att kryssa i den svarta rutan. Esteban kryssar först i de röda rutorna, sedan de lila och sedan resten i den ordningen pilerna indikerar:

(b) Nej, Esteban kommer aldrig lyckas oavsett hur Chiyen börjar. Låt oss undersöka vad som skulle hända om han faktiskt lyckades.

Vi kommer titta på figuren som ikryssade rutor bildar och undersöka dess omkrets. Från början är det bara en ruta som är ikryssen och omkretsen av den figuren är 4.

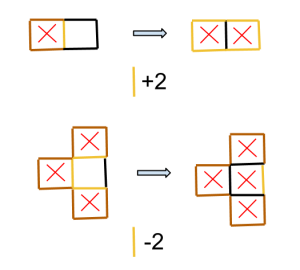
I fortsättningen kan Esteban kryssa i rutor som har antingen 1 ikryssad granne eller 3 inkryssade grannar. I första fallet kommer omkretsen av figuren öka med 2, i andra fallet minska med 2.

Omkretsen ska i slutändan sammanfalla med hela rektangelns omkrets, det vill säga vara lika med 36. Kan Esteban gå från 4 till 36 genom att ibland öka med 2 och ibland minska med 2? Ja, teoretiskt sett, men eftersom totalt sett så ökar vi med 32, så måste ökningar med 2 ske 16 gånger fler än minskningar. Det betyder att antalet ökningar/minskningar är ett jämnt tal. Men antalen steg måste vara udda, eftersom det är 79 rutor Esteban ska kryssa i. Motsägelse.