Har du läst om hur man hittar pythagoreiska tripplar i cirklar? I artikelserien träffar vi på många cirklar som har några punkter med heltalskoordinater på periferin.
Men oftast är antalet punkter delbart med 4 (cirkeln är centralsymmetrisk i förhållande till koordinatsystemet, eftersom mittpunkten ligger i vårt fall antingen i en heltalsnod eller i mitten av en ruta). Men kan vi hitta en cirkel med ett annat antal punkter på periferin, t.ex. 6?
Vi vill alltså ta reda på för vilka n det går att hitta en cirkel som går igenom exakt n heltalspunkter.
Går det att hitta en cirkel med en heltalsnod på periferin? Så klart går det, vi kan t.ex. ta en cirkel med en väldigt liten radie som går igenom en godtycklig punkt.
Två heltalsnoder på periferin då? Ja, vi kan ju skapa cirklar som inte är rotationssymmetriska, men däremot spegelsymmetriska, genom att välja att ha mittpunkten på cirkeln i (0, 0.5) till exempel eller egentligen var som helst mellan två närliggande heltalsnoder. Tar vi radien lika med 0.5 så är vi garanterade att inga andra heltalsnoder än (0,0) och (0,1) kommer med på cirkelns periferi.
Hur gör vi med 3 punkter på periferin? Cirkeln får nu varken vara spegelsymmetrisk eller rotationssymmetrisk med avseende på heltalsnoderna (om två periferipunkter ligger strikt på vänstra/högra halvan av cirkeln). Således måste vi placera mittpunkten varken i en heltalspunkt eller i en ”halvtalspunkt”. Under några antaganden kan vi försöka hitta en cirkel med två heltalspunkter som befinner sig på samma vertikala linje. Vi antar att cirkelns horisontella diameter ligger på linjen y=0.
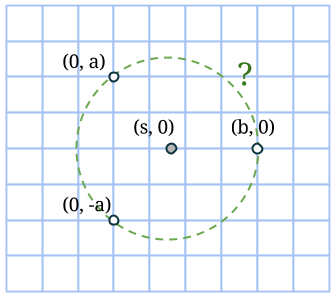
Koordinaterna för mittpunkten är då (s, 0) och för heltalsperiferipunkterna (0, a), (0, -a) samt (b, 0). Då får vi likhet av två radier (i kvadrat):
s2 + a2 = (b – s)2
s2 + a2 = b2 – 2bs + s2
a2 = b2 – 2bs
Både a och b är positiva heltal, medan s är ett positivt reellt tal (förmodligen större än 1). Därför måste b vara åtminstone 3 och vi prövar b = 3.
Då måste a2 = 9 – 6s. Tar vi a = 1 får vi s = 4/3 vilket ger oss cirkeln:
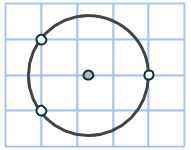
Denna har exakt 3 punkter på periferin! Men hur gör man i det allmänna fallet? Kan man alltid få relativt snygga cirklar, det vill säga där punkterna ligger i par på respektive vertikallinjer? Det visar sig att man kan det med hjälp av Schinzels sats!
Schinzels sats
Det existerar en cirkel med exakt n heltalspunkter på periferin för varje naturligt tal n.
För jämna n=2k har Schinzels cirkel ekvationen
Medan för udda n=2k+1 har Schinzels cirkel ekvationen
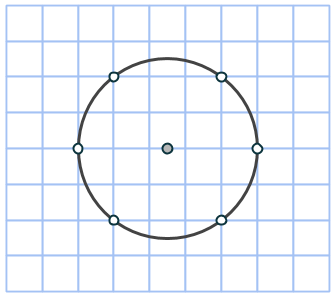
Testa till exempel hur cirkeln med exakt 7 heltalspunkter på periferin ser ut!
Schinzels cirklar är inte nödvändigtvis de minsta med den egenskapen, men de är i alla fall snygga på sättet beskrivet innan, nämligen att heltalspunkterna på periferin förekommer i par, vilket kan ses från ekvationen (mittpunkten ligger på en horisontell heltalslinje).
Kan du bevisa att Schinzels cirklar uppfyller egenskaperna som det påstås i satsen? Helt trivialt är det ju inte att bevisa.
Tack Sture Sjöstedt för frågeformuleringen, samt länkar och tips!

Hej Valentina!
Känner du till vilka som först löste Carrolls problem:
Att finna tre pythagoreiska trianglar med samma area ?
Hälsningar
Sture
Hej Sture!
Nej, det känner jag inte till tyvärr! Menar du hittade de första tre trianglarna eller ett allmänt uttryck?
Hej Valentina!
Det finns en allmän metod. Dag Johnson skrev att den kan ha varit känd redan på
Babylonisk tid. I en PDF-fil jag sänt dig gör jag en härledning av hur man kan
komma fram till en generell metod att finna tripplar av Pythagoreiska trianglar
med samma area. Ett par kvadrupler dyker också upp i den lista jag lät datorn
ta fram 1999. Se Elementa nr2 99.
Ja, precis, man kan leka med trianglarna här t.ex.: http://demonstrations.wolfram.com/PythagoreanTrianglesWithTheSameArea/
Men jag har inte hittat när det upptäcktes för första gången.
Hej Val!
I Paul Yius PDF Recreational Mamthematics uppges att Diofantos kände till lösningar
till det problem som numera kallas Carrolls problem.
Är det inte så att man kan hitta tripplar med samma area bland Heronska trianglar också?
Hej Sture!
Jo, visst finns det, till och med finns det tripplar med samma area OCH omkrets.
På den här sidan finns exempel och förklaringar: http://www.se16.info/hgb/triangleareaperimeter.htm
Jag tyckte också att det var roligt att trianglarna med sidorna (5,5,6) respektive (5,5,8) har samma area 12.
För Heronska trianglar av typen m-1, m, m+1 kan finna alla trianglar av den typen.
Kan man hitta ett system för att finna alla Heronska trianglar av typen m-11, m, m+11?
Hej Sture, jag tror inte jag riktigt förstår din fråga. Menar du vilka trianglar av typen m-11, m, m+11 existerar överhuvudtaget? Eller de som har samma area som en annan Heronsk triangel?
Hej Val, jag menar: Finns det en enkel rekursionsformel av Fibonnacityp såsom det finns då trianglarna är av m – 1, m , m + 1 typ. Jag tror att det behövs två olika formler.
Hej Val! Schinzel’ sats ger den minsta cirkel som har fyra gitterpunkter. Den med radien kvadratroten ur två och centrum i origo har fyra gitterpunkter.
Här får du en intressant tabell. Vill du förlänga den multiplicerar du med nästa primtal av typen 4k + 1
Cirkelns Radie :2^(1/2), 5, 65, 1105, 20995, 22527635, 833522495
Antal gitterpunkter: 4,— 12, 36, 108, 324, 972, 2916
Oj, tufft resultat Sture! Hur kommer det sig?
Intuitivt så borde det ha att göra med primfaktorisering av gaussiska heltal. Ett primtal p på formen 4k+1 kan faktoriseras (m.a.p. gaussiska heltal, dvs tal på formen x+iy där x och y är heltal) som (a+bi)(a-bi) på ett unikt sätt (upp till multiplikation med i) där både a+bi och a-bi är primelement i ringen av gaussiska heltal. För att ett gaussiskt heltal z ska ha absolutbelopp r så måste z*conj(z) vara r^2. Om vi låter z vara primfaktoriserad som x_1*x_2*… i ringen av gaussiska så måste conj(z), z:s konjugat ha samma faktorisering (fast konjugerad). I vårt fall så är r en produkt av olika heltalsprimtal (på formen 4k+1) så vi vet dess gaussiska faktorisering. För att återfå möjliga alternativ till z så borde man kunna plocka ut gaussiska primfaktorer ur s^2 och samtidigt ”ge” konjugatet till conj(z). Då våra faktorer uppträder i kvadruppler (a+bi)(a+bi)(a-bi)(a-b) så finns tre möjligheter, z får (a+bi)^2, z får (a-bi)^2, eller z får (a+bi)(a-bi). Detta förklarar faktorn 3 när vi multiplicerar radien med primtal på formen 4k+1.
Tack Johan H
Din teori stämmer exakt vad jag kommit fram till genom att finna tre startvärden och sedan starta en rekursion
Det är en diofantisk ekvation av typen x^2 + n*y^2 = P du skriver om. Jag har också lösningar för n=2 och n=3.
där är faktorn 2, inte 3 som för cirklar
Johan B
Diofantos har en dubbel Pythagoras som fungerar på samma sätt som multiplikation av komplexa tal.
(3 + 4i)(5 + 12i ) = 39 + 52i
Johan B
Hur många primitiva rätvinkliga trianglar med hypotenusan 65 finns det?
Det går att hitta på lite olika sätt, ifall vi fortsätter på gaussiska heltal-temat så kan vi använda att gaussiska heltal z=a+bi med |z|=r som motsvarar ickeprimitiva trianglar kan faktoriseras som något heltal (>1) n*(c+di). Speciellt så har vi i en situation som tidigare där z*conj(z)=r^2 där r är en produkt av olika primtal på formen 4k+1 att n i sin tur har för varje faktor a+bi har en faktor a-bi. Vi vill undersöka de som saknar denna egenskap, dvs då vi för varje primtal p (på formen 4k+1) har p^2=(a+bi)^2(a-bi)^2 där a+bi samt dess konjugat är primelement så måste z tilldelas antingen faktorn (a+bi)^2 eller faktorn (a-bi)^2 (då att tilldela den faktorn (a+bi)(a-bi)=p skulle innebära en ickeprimitiv). Dvs varje extra primfaktor ger en dubblering av möjligheter. Vi startar med 4 möjligheter för cirkeln med radie 1.
Dvs på en cirkel med radie r där r är en produkt av m st olika primtal på formen 4+1 så finns det 4*2^m gitterpunkter som motsvarar primitiva trianglar. Dessa trianglar uppkommer dock flera ggr, så vi måste dividera med 8 (först dividera med 4 för att vi bara vill räkna dem i första kvadranten, och sedan med 2 för att a+bi och b+ai ger samma triangel).
För specialfallet 65=13*5 så får vi alltså 2 möjligheter. Om vi minns faktoriseringar av 5 och 13 (5=(2+i)(2-i) och 13=(3+2i)(3-2i)) så kan vi lätt få fram de två genom att beräkna (2+i)^2(3+2i)^2=56i-33 samt (2+i)^2(3-2i)^2=63-16i att motsvarande pythagoreiska tripplar är 33,56,65 samt 16,63,65.
Det borde gå att få fram rätt lätt med teorin för pythagoreiska tripplar också (eller ännu lättare genom att kolla http://www.tsm-resources.com/alists/trip.html men det känns som fusk…).
Johan B
Man behöver inte plocka in komplexa tal när man tar upp detta i grundskolan och gymnasiet. Jag skrev lite om detta i Elementa 1999 nr1 och nr2. 1975 publicerades ett Babyloniskt räkneschema som nedtecknats av Theon från Smyrna i Elementa. Det ger koefficienten för sqrt(2) och den kända termen när man beräknar följande binom upphöjt till n. (sqrt(2) + 1)^n. Effekten är att Pascals triangels triangel krymper till en xy-tabell. Genom att kombinera Lucastalen och Fibonaccitalen kan man lösa ett par andra Diofantiska andragradsekvationer. Vilka?