Val i Bananrepubliken
[kkratings]
I riksdagsvalet i Bananrepubliken deltog alla landets medborgare. Alla som röstade på Clementinpartiet tycker om clementiner. Bland dem som röstade på de andra partierna tycker 90% inte om clementiner.
Hur stor procent röster fick Clementinpartiet i valet om 46% av Bananrepublikens invånare tycker om clementiner?

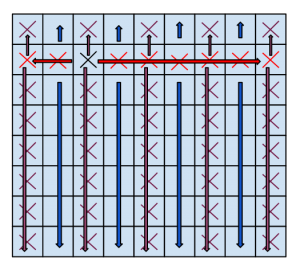
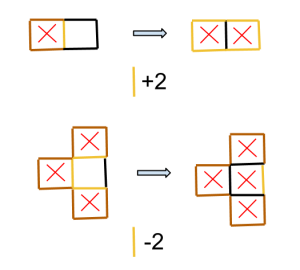
Kryssa grannrutor
Kryssa grannrutor
[kkratings]
Chiyen satte ett kryss i en ruta på en rektangel. Esteban får sätta kryss i de andra rutorna, men bara om de uppfyller följande regel: man får bara kryssa i rutor som har ett udda antal grannrutor med kryss (med grannrutor menas de som delar en sida med rutan).
Kan Esteban kryssa i alla rutorna på rektangeln, oavsett vilken ruta som blev ikryssat av Chiyen, om rektangeln har storleken:
(a) 8×9 rutor?
(b) 8×10 rutor?

Bilar i Mexico
Bilar i Mexico
[kkratings]
Mexico bestämde sig för att införa en ny lag, som innebär att varje bil i landet måste stå obrukad minst en dag i veckan (ägaren måste meddela polisen vad registreringsnumret är och vilken veckodag bilen inte kommer vara i bruk).
I en viss mexikansk familj vill vuxna åka bil varje dag (var och en behöver en bil för att utföra egna ärenden). Hur många bilar måste de som minst ha, om det finns
(a) 5 vuxna
(b) 8 vuxna
i den familjen?
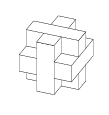
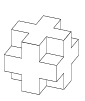
Rubiks kub utan hörn
Rubiks kub utan hörn
[kkratings]
Man tog bort alla hörn från en Rubiks kub. Skulle en sådan konstruktion kunna sättas ihop av rätblock med 1×3-kuber?
Kulor i olika färger
Kulor i olika färger
[kkratings]
Tre personer A, B och C räknade antalet julgranskulor av olika färger på granen. Var och en kunde skilja på två av färgerna, men de andra två kunde hen förväxla: En av dem förväxlade ibland röd och rosa, en annan kunde förväxla rosa och beige, och den tredje av dem kunde förväxla beige och gul. De sammanställde olika antal som de kom fram till i en tabell. Hur många kulor av varje färg fanns i granen på riktigt?
| Röd | Rosa | Beige | Gul | |
| A | 2 | 5 | 7 | 9 |
| B | 2 | 4 | 9 | 8 |
| C | 4 | 2 | 8 | 9 |
Tätt med punkter på linjen
Tätt med punkter på linjen
[kkratings]
På en linje fanns några punkter. Man gjorde det mer tätt mellan punkterna: det sattes ut en ny punkt i varje mellanrum mellan två gamla punkter. Man gjorde det tätare mellan punkterna på samma sätt en gång till och sedan en sista gång (totalt tre gånger).
Efter hela processen fanns det 113 punkter på linjen. Hur många punkter fanns på linjen från början?
Tretton punkter
Tretton punkter
[kkratings]
Dra fem streck utan att lyfta pennan från pappret så att strecken går igenom alla 13 punkterna:

Följder med regel
Följder med regel
[kkratings]
Du får se två följder med tal:
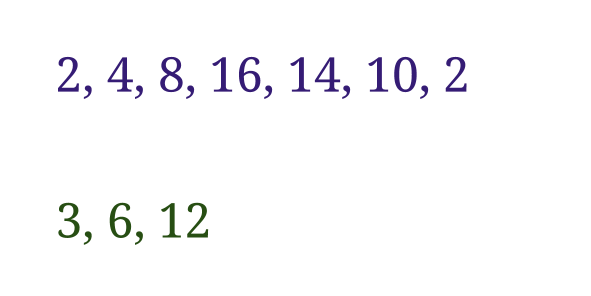
Det finns en regel som utifrån varje tal bestämmer nästa tal.
(a) Vad är det för regel?
(b) Bestäm alla positiva heltal som enligt regeln blir sig själva.
(c) Visa att talet 22012 kommer att bli ensiffrigt om man tillämpar regeln tillräckligt många gånger.
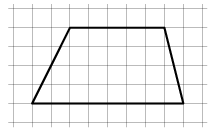
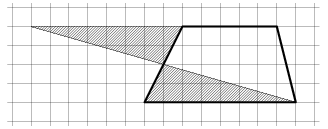
Trapets till en triangel
Trapets till en triangel
Ett tal med åtta siffror
Ett tal med åtta siffror
[kkratings]
Kan man hitta på ett tal som består av 8 olika siffror, så att talet är delbart med alla siffror som ingår i det?

© 2009-2025 Mattebloggen